引言
大型语言模型(LLMs)在解决复杂的推理任务方面展现出日益强大的能力,例如应对**数学奥林匹克竞赛难题、科学问答以及多步骤逻辑谜题**[3,8]。然而,这些模型的性能是否已臻完美?尽管它们确实强大,但目前在测试阶段仍存在计算成本高昂且效率低下的问题[5,6]。为了应对这一挑战,**Meta AI** 的研究人员提出了一项创新解决方案,名为“**DeepConf**”,亦称“**深度置信推理(Deep Think with Confidence)**”[1]。
多数投票下的“自洽性”挑战
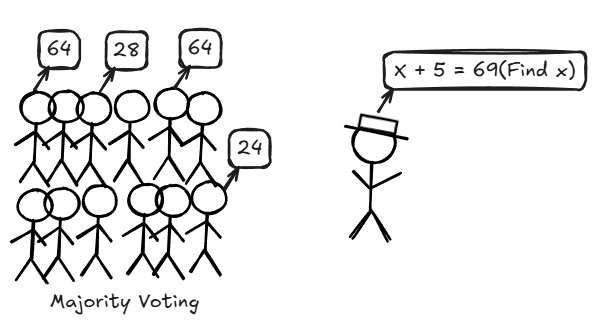
实践中,这一问题究竟如何体现?可以设想一个拥有100名学生的教室,他们被要求在一个小时内解决一道复杂的奥林匹克数学难题。时间结束后,可以收集所有答案并进行投票——得票最多的答案“获胜”。
(来源:作者)
这正是大型语言模型(LLMs)中多数投票自洽性问题的工作原理[2,3]。模型并非只提供一个解决方案,而是探索数百条推理路径(例如,512个不同的分步解决方案),然后选择出现频率最高的答案。
在**AIME 2025数学基准测试**中,**Qwen3-8B**模型单次尝试(称作pass@1)的准确率约为**68%**,这相当于只采纳一名学生的答案。但如果为每个问题生成**512条推理轨迹**(称作conf@512)并采取多数投票结果,准确率将跃升至**82%**[1,4]。
这听起来很棒,对吗?然而,问题在于额外的511条轨迹会产生近**1亿个额外token**,并且更多的轨迹并非总能带来帮助;当低质量的解决方案在投票中占据主导时,性能有时会保持不变甚至下降[1,7,8]。换句话说,如果学生们只是随机猜测,那么全班的投票结果并不能反映出教室里最优秀的思考者[1]。
研究人员的早期尝试:利用内部不确定性信号
研究人员试图通过分析模型的内部不确定性信号来解决上述问题。这种内部不确定性信号,可以类比为每隔一段时间(例如每5分钟)检查学生是否正在按正确的小步骤进行解题。模型会查看每个token的概率分布,并计算其在特定时间点上的置信度或熵。如果模型具有高置信度或低熵(即分布集中且峰值高),则表明模型对其特定token的预测非常确定,反之亦然[1,11]。
通过整合整个推理轨迹中这些token级别的预测统计数据,可以评估解决方案的**“可信度”**。研究人员还可以在多数投票之前过滤掉低置信度的轨迹——就像忽略那些明显是猜测的学生答案一样。这样做能够**减少无效投票,提升结果的稳健性**[1]。

(来源:作者)
然而,这些方法仍然是全局性的,并未完全解决效率问题[1,6,13]。
接下来,将探讨一些相关的数学概念,例如token熵、token置信度和轨迹置信度的工作原理[1,11]。
Token熵(Token Entropy):
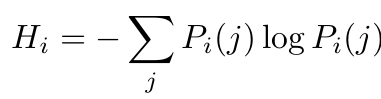
(来源:作者)
这个熵值可以这样理解:**logPᵢ(j)**项表示了在第i个位置上token预测的“意外程度”,其中Pᵢ(j)是该token的概率。当概率为1时(模型完全确定,意外程度为0,没有不确定性),表明模型对该token预测的置信度极高。然后,取所有token熵的平均值,即可定义每个步骤或token预测的熵[1]。
Token置信度(Token Confidence):
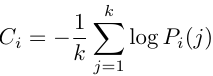
(来源:作者)
Token置信度衡量的是模型对每个token预测的确定程度(可以视为“反意外程度”指标)[1]。
平均轨迹置信度(Average Trace Confidence):
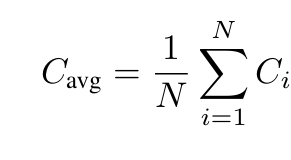
(来源:作者)
在计算每个token的置信度时,这些置信度分数的平均值即代表了整个轨迹的置信度[1]。
置信度感知测试时间缩放:DeepConf
DeepConf进一步发展了这一理念,它并非简单地生成数百个解决方案然后进行投票[2,3,12]。该方法在生成过程中和生成之后都会考量模型的内部置信度信号。它能够动态地过滤掉低质量的推理轨迹,无论是实时进行(在线模式)还是在所有解决方案生成完毕后进行(离线模式)。DeepConf只保留最可信的推理路径,从而减少了不必要的计算浪费[1,6]。
那么结果如何呢?在AIME 2025测试中,采用GPT-OSS-120B模型的DeepConf@512实现了惊人的99.9%准确率。相比之下,纯多数投票的准确率为97.0%,而单次尝试(pass@1)仅达到91.8%。同时,与蛮力并行思考相比,DeepConf将token生成量**减少了高达84.7%**[1,6,7]。
在对基本概念有了清晰的理解后,现在将深入探讨这些置信度衡量指标的具体工作原理。
组置信度(Group Confidence):
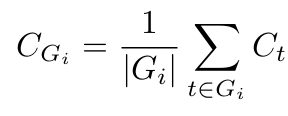
(来源:作者)
Cₜ 依然代表token级别的置信度。组置信度(CGᵢ)可被视为对确定性的一种“局部放大”检查,其中|Gᵢ|表示重叠窗口内(例如1024或2048个token)前一个token的数量。这为我们提供了确定性的局部快照[1]。
底部10%组置信度(Bottom 10% Group Confidence):
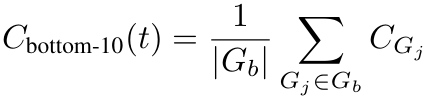
(来源:作者)
当对组置信度分数进行排序并聚焦于底部10%时,实际上是在突出推理链中的最薄弱环节。如果这些步骤看起来不够稳固,就可以将其剔除以节省计算资源[1]。
尾部置信度(Tail Confidence):
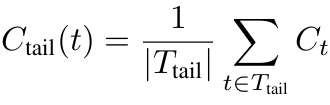
(来源:作者)
尾部置信度概念简单直观;它计算的是模型对最后固定数量的token(例如2048个)的置信程度(检查“最后一公里”),这对于预测正确结论至关重要[1]。
DeepConf可以在两种模式下使用:离线模式和在线模式[1]。
基于置信度的离线推理
在离线模式下,无需反复调用模型或获取额外数据。此时,处理的只是已经生成好的轨迹。
其挑战在于如何从这些已有的轨迹中提炼出最可靠的答案。
在离线模式中,可以对结果轨迹进行简单投票(当存在大量噪声结果时可能失效),也可以采用置信度加权多数投票。后者通过计算轨迹的平均置信度值,并将其与该解决方案的出现次数相乘来决定权重[1,2]。
置信度过滤与投票:在投票之前,首先丢弃置信度最低的轨迹。即先根据置信度筛选轨迹(保留前n%的轨迹),然后再进行简单投票或加权置信度投票[1,9,10]。
可以根据需求选择合适的置信度指标,例如平均置信度、组置信度或尾部置信度[1,10,11]。

离线推理算法1(来源:Deep Think with Confidence[1])
分步解释:
输入:
提示P:希望得到答案的问题或输入。
轨迹数量N:将生成的推理路径数量。
过滤阈值𝜂:用于筛选顶部轨迹的百分比。
置信度测量C(t):用于计算轨迹置信度分数的任意方法[1]。
初始化:
创建一个空集合T。
创建一个空置信度集合C[1]。
生成轨迹:
对于从1到N的每次迭代:为提示P生成一条轨迹tᵢ。
计算置信度分数 Cᵢ = C(tᵢ)。
将(tᵢ, Cᵢ)对存储在T和C中[1]。
过滤高置信度轨迹:
从所有N条轨迹中,根据它们的置信度分数选择前η%的轨迹。
这会移除噪声或低质量轨迹,只保留强置信度的答案[1]。
投票:
可以为每个可能的答案a计算投票分数V(a)。
这可以是简单的计数或加权投票[1]。
选择最终答案:
选择投票分数最高的答案â[1]:
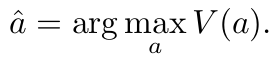
(来源:作者)
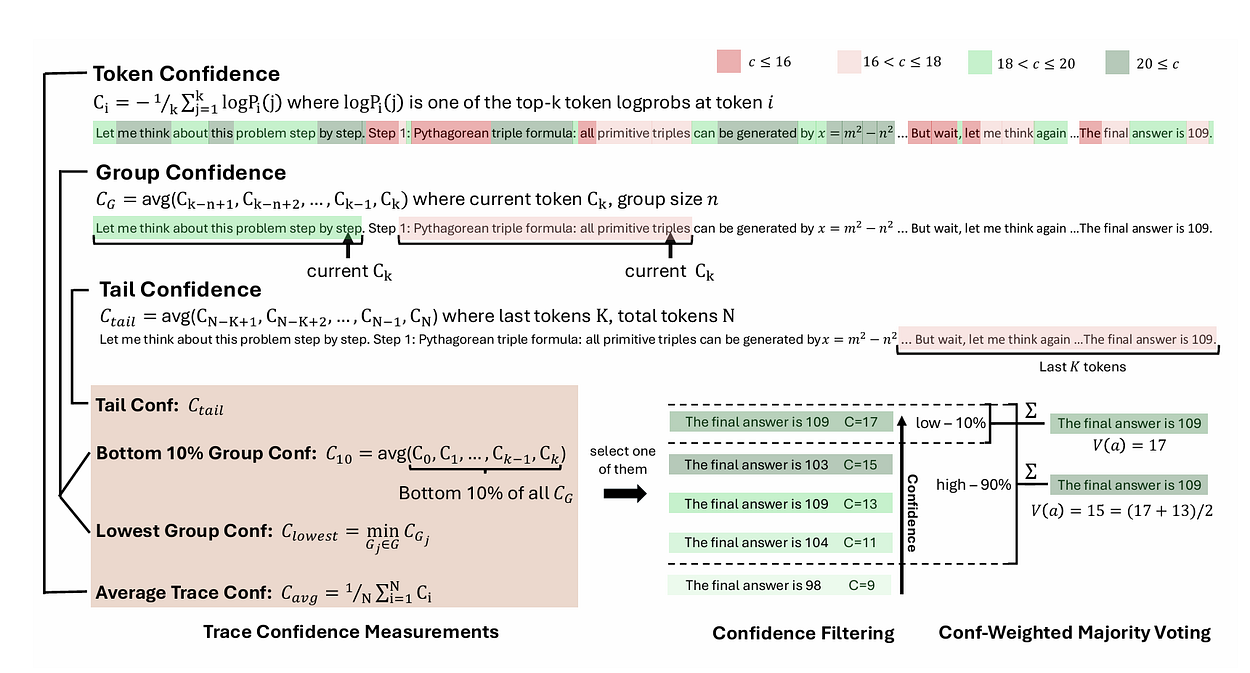
置信度测量与离线置信度推理(来源:Deep Think with Confidence[1])
基于置信度的在线推理
该算法能够即时生成轨迹,并在拥有足够证据时动态地测量置信度[1,5,14,15]。
算法描述:

在线推理算法2(来源:Deep Think with Confidence[1])
分步解释:
1. 输入
提示P:待回答的问题。
轨迹预算B:希望生成的最大轨迹数量。
初始轨迹Nᵢₙᵢₜ:用于“预热”的起始轨迹池。
过滤阈值η:保留高置信度轨迹的数量百分比。
共识阈值τ:一个百分比值,表示当对多数答案有足够信心时可以停止生成[1]。
2. 离线预热
在在线生成之前:
使用Nᵢₙᵢₜ条轨迹运行算法1。
计算置信度阈值s:
取初始轨迹置信度分数的100-η百分位值。
这定义了token/组被考虑所需的最低置信度。
使用初始轨迹初始化轨迹集合T,并计算所有答案的初始投票值V(a)[1]。
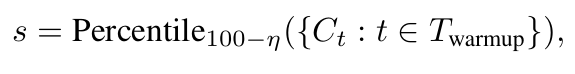
(来源:作者)
确定初始多数答案â[1]。
3. 在线生成循环
当以下两个条件均成立时:
当前多数答案的置信度尚未达到足够水平:
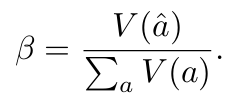
(来源:作者)
且尚未超出轨迹预算|T|<B
→ 继续生成新的轨迹[1]:
4. 逐步生成轨迹
在生成轨迹t时:逐token生成。
在每个token i之后,计算该token/组的组置信度C_Gᵢ。
如果C_Gᵢ<s:停止生成该轨迹(置信度低)。
否则:将token i添加到轨迹t[1]。
5. 更新
将已完成的轨迹t添加到轨迹集合T。
计算轨迹置信度Cₜ。
更新所有答案的投票计数V(a)。
更新多数答案â[1]。
6. 终止
当满足以下任一条件时停止:
多数答案â达到的共识超过阈值τ。
或轨迹预算B已达到。
返回最终的多数答案â[1]。
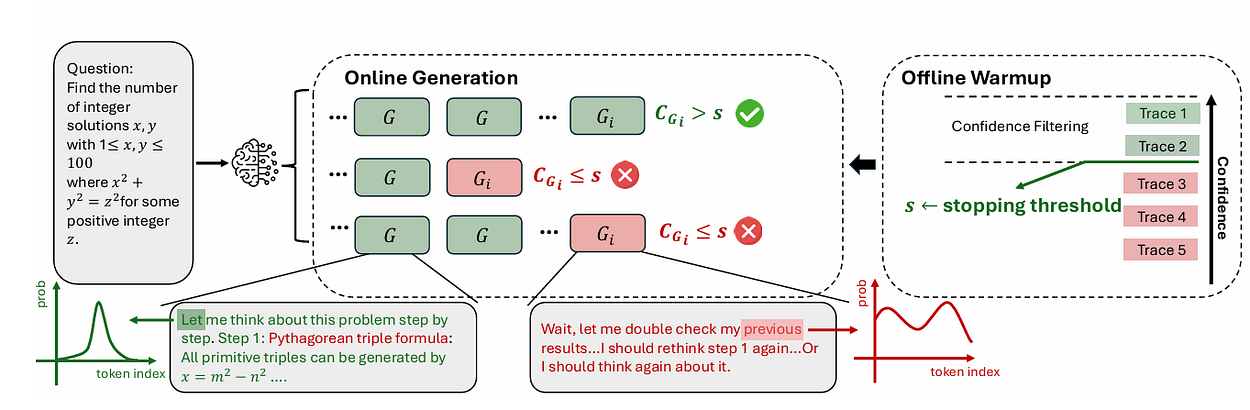
DeepConf在线生成过程(来源:Deep Think with Confidence[1])
这项算法体现了提前停止的艺术,从而节省了大量的计算和资源[1,5,6,7,13,14]。
结论
那么,这项研究的启示是什么?即使是AI领域中最“聪明”的“学生”,有时也需要一点“自我怀疑”才能真正闪耀。DeepConf展示了“自我怀疑”的强大力量。通过选择更智能、基于置信度的方法,而非蛮力计算,可以节省数百万计的计算资源。这就像将一场混乱的数学竞赛,转变为一支沉着冷静的专家解题团队。
随着AI不断学习如何带着置信度进行思考,正迈向一个未来:模型不仅更智能,也更经济,耗费更少的计算资源,减少错误,并以每个token提供更多的“脑力”。谁知道呢?也许有一天,您最喜爱的模型会成为您最节俭、最具自我意识的学习伙伴。在此之前,让持续思考如何更智能地工作,而不是更辛苦地工作。
参考文献
[1] Dayananda, A., Sivasubramanian, S., & Bartlett, P. (2024). Deep Think with Confidence: Confidence-Aware Test-Time Scaling for Better Alignment. arXiv preprint arXiv:2508.15260. 检索自 https://arxiv.org/pdf/2508.15260
[2] Wang, X., Wei, J., Schuurmans, D., Le, Q., Chi, E., Narang, S., Chowdhery, A., & Zhou, D. (2022). Self-consistency improves chain-of-thought reasoning in language models. arXiv preprint arXiv:2203.11171.
[3] Wei, J., Wang, X., Schuurmans, D., Bosma, M., Xia, F., Chi, E., Le, Q. V., Zhou, D., & others. (2022). Chain-of-thought prompting elicits reasoning in large language models. In Advances in neural information processing systems (Vol. 35, pp. 24824–24837).
[4] Art of Problem Solving. (2025a). 2025 AIME I. https://artofproblemsolving.com/wiki/index.php/2025AIMEI. 访问日期:2025。
[5] OpenAI. (2024). OpenAI o1 system card. arXiv preprint arXiv:2412.16720.
[6] Snell, C., Lee, J., Xu, K., & Kumar, A. (2024). Scaling LLM test-time compute optimally can be more effective than scaling model parameters. arXiv preprint arXiv:2408.03314.
[7] Brown, B., Juravsky, J., Ehrlich, R., Clark, R., Le, Q. V., Ré, C., & Mirhoseini, A. (2024). Large language monkeys: Scaling inference computation with repeated sampling. arXiv preprint arXiv:2407.21787.
[8] Chen, L., Davis, J. Q., Hanin, B., Bailis, P., Stoica, I., Zaharia, M., & Zou, J. (2024a). Are more LLM calls all you need? towards scaling laws of compound inference systems. https://arxiv.org/abs/2403.02419
[9] Aggarwal, P., Madaan, A., Yang, Y., et al. (2023). Let’s sample step by step: Adaptive consistency for efficient reasoning and coding with LLMs. arXiv preprint arXiv:2305.11860.
[11] Fadeeva, E., Rubashevskii, A., Shelmanov, A., Petrakov, S., Li, H., Mubarak, H.,… & Panov, M. (2024). Fact-Checking the Output of Large Language Models via Token-Level Uncertainty Quantification. arXiv preprint arXiv:2403.04696.
[13] Li, Y., Yuan, P., Feng, S., Pan, B., Wang, X., Sun, B.,… & Li, K. (2024). Escape sky-high cost: Early-stopping self-consistency for multi-step reasoning. arXiv preprint arXiv:2401.10480.
[14] Han, Z., Li, Z., Wang, Y., Guo, C., Song, R., He, J.,… & Chen, W. (2024). Adaptive Inference-Time Compute: LLMs Can Predict if They Can Do Better, Even Mid-Generation. arXiv preprint arXiv:2410.02725.






