强化学习(RL)为各类序列决策问题提供了强大的解决方案。其中,时序差分学习(Temporal-Difference Learning,简称TD学习)方法是强化学习算法中一个备受欢迎的子集。TD学习方法巧妙地结合了蒙特卡洛(Monte Carlo)方法和动态规划(Dynamic Programming)方法的关键特点,能够在无需完美环境动力学模型的情况下,显著加速学习过程。
本文将在一个定制的网格世界(Grid World)中,详细比较不同类型的TD算法。实验设计旨在凸显持续探索的重要性,并深入分析所测试算法的各自特性,包括:Q-learning、Dyna-Q以及Dyna-Q+。
本文内容纲要如下:
- 环境描述
- 时序差分(TD)学习概述
- 无模型TD方法(Q-learning)与基于模型TD方法(Dyna-Q和Dyna-Q+)
- 实验参数设定
- 性能比较分析
- 结论
用于复现本文结果和图表的完整代码可在此处获取:https://github.com/RPegoud/Temporal-Difference-learning
实验环境:网格世界
本实验中使用的环境是一个具备以下特点的网格世界:
- 网格尺寸为12行8列。
- 智能体从网格的左下角开始,目标是到达位于右上角的宝藏(一个奖励为1的终止状态)。
- 蓝色传送门相互连接,通过位于单元格(10, 6)的传送门将传送到单元格(11, 0)。智能体在首次传送后不能再次使用该传送门。
- 紫色传送门仅在100个回合后才会出现,但它能让智能体更快地到达宝藏。这一设计鼓励智能体持续探索环境。
- 红色传送门是陷阱(奖励为0的终止状态),会结束当前回合。
- 撞到墙壁会导致智能体停留在原地。
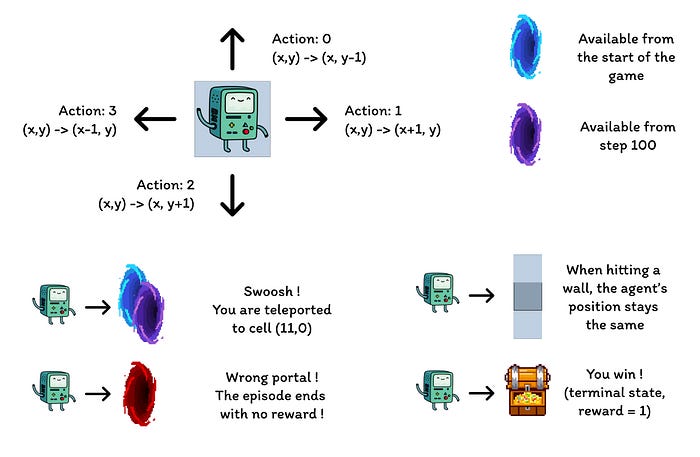
网格世界中不同组件的描述(作者绘制)
本次实验旨在比较Q-learning、Dyna-Q和Dyna-Q+智能体在动态变化环境中的行为。在100个回合后,最优策略将发生改变,成功回合中的最优步数将从17步减少到12步。
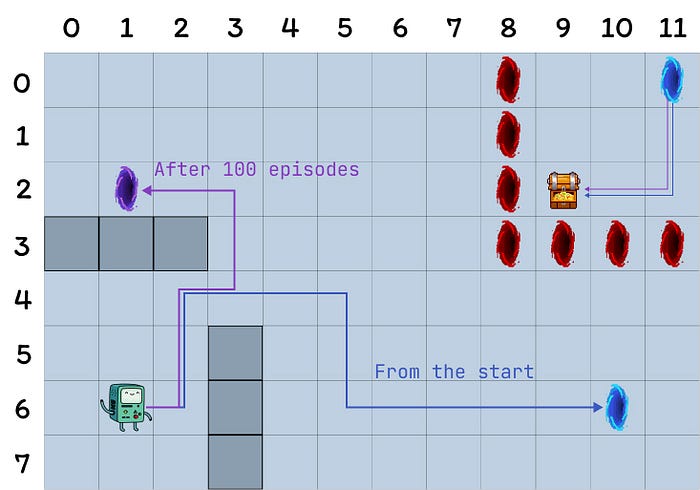
网格世界的表示,最优路径取决于当前回合(作者绘制)
时序差分学习(Temporal-Difference Learning)简介
时序差分学习(TD学习)结合了蒙特卡洛(MC)方法和动态规划(DP)方法的特点:
- 与蒙特卡洛方法类似,TD方法可以从经验中学习,无需环境的动力学模型。
- 与动态规划方法类似,TD方法在每一步之后基于其他已学习的估计值更新其估计,而无需等待最终结果(这被称为自举或bootstrapping)。
TD方法的一个显著特点是,它们会在每个时间步更新其价值估计,这与蒙特卡洛方法需要等到回合结束才能更新不同。
事实上,这两种方法具有不同的更新目标。蒙特卡洛方法旨在更新回报Gt,而这只有在回合结束时才可用。相比之下,TD方法的目标是:
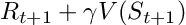
TD方法的更新目标
其中,V是对真实价值函数Vπ的估计。
因此,TD方法结合了蒙特卡洛的采样特性(通过使用真实价值的估计)和动态规划的自举特性(通过基于依赖于进一步估计的估计来更新V)。
时序差分学习最简单的版本被称为TD(0)或一步TD,其具体实现通常如下所示:
![TD(0)算法的伪代码,摘自《强化学习:导论》[4]](/2025/10/03/66a451082c25fb14dca7f4cee1047da0.png)
TD(0)算法的伪代码,摘自《强化学习:导论》[4]
当从状态S转换到新状态S’时,TD(0)算法会计算一个回溯价值并相应地更新V(S)。这个回溯价值被称为TD误差,即观测到的奖励R加上新状态的折扣价值γV(St+1)与当前价值估计V(S)之间的差值:
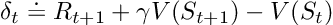
TD误差公式
总而言之,TD方法具有以下几个优点:
- 它们不需要环境动力学的完美模型p。
- 它们以在线方式实现,在每个时间步后更新目标。
- 如果学习率α(学习步长)遵循随机近似条件(详情请参阅《强化学习:导论》[4]第55页“跟踪非平稳问题”),TD(0)被保证对任何固定策略π收敛。
实现细节
以下章节将探讨几种TD算法的主要特性及其在网格世界中的性能表现。
为简化比较,所有模型均使用了相同的参数设定:
- Epsilon (ε) = 0.1:ε-贪婪策略中选择随机动作的概率。
- Gamma (γ)= 0.9:应用于未来奖励或价值估计的折扣因子。
- Alpha(α) = 0.25:限制Q值更新的学习率。
- 规划步数= 100:对于Dyna-Q和Dyna-Q+,每次直接交互后执行的规划步数。
- Kappa (κ)= 0.001:对于Dyna-Q+,规划步长中应用的奖励附加值的权重。
每种算法的性能首先以单次运行400个回合的结果呈现(Q-learning、Dyna-Q和Dyna-Q+章节),随后在“总结与算法比较”章节中,对100次运行(每次250个回合)的结果进行平均分析。
Q-learning算法
此处实现的第一个算法是著名的Q-learning(Watkins, 1989):
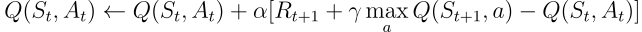
Q-learning被称为离策略(off-policy)算法,因为它直接致力于近似最优价值函数,而非智能体所遵循的策略π的价值函数。
实践中,Q-learning仍然依赖于一个策略,通常称为“行为策略”,来选择要访问和更新的状态-动作对。然而,Q-learning之所以是离策略的,是因为它根据未来奖励的最佳估计来更新Q值,而无论所选择的动作是否遵循当前策略π。
与之前的TD学习伪代码相比,Q-learning主要有三个不同点:
- 需要为所有状态和动作初始化Q函数,且Q(终止状态)应为0。
- 动作是根据基于Q值的策略选择的(例如,相对于Q值的ε-贪婪策略)。
- 更新目标是动作价值函数Q,而不是状态价值函数V。
![Q-learning算法的伪代码,摘自《强化学习:导论》[4]](/2025/10/03/98c57e8156025b7bfda1d0fd657f1ed7.png)
Q-learning算法的伪代码,摘自《强化学习:导论》[4]
在第一个算法准备好测试之后,训练阶段便可开始。智能体将根据其相对于Q值的ε-贪婪策略在网格世界中导航。该策略以(1 – ε)的概率选择Q值最高的动作,并以ε的概率选择随机动作。每次执行动作后,智能体将更新其Q值估计。
通过热力图,可以可视化网格世界中每个单元格的最大动作价值估计Q(S, a)的演变。在此实验中,智能体进行了400个回合。由于每个回合只进行一次更新,Q值的演变相当缓慢,大部分状态仍未被充分探索:
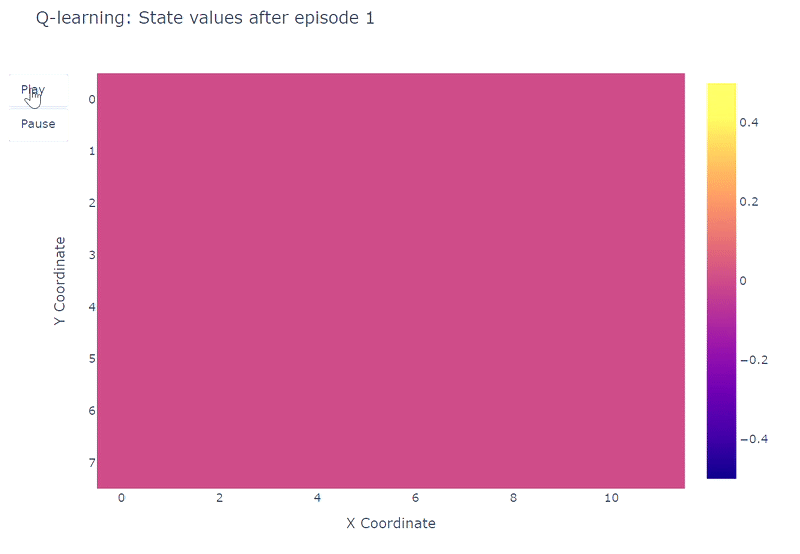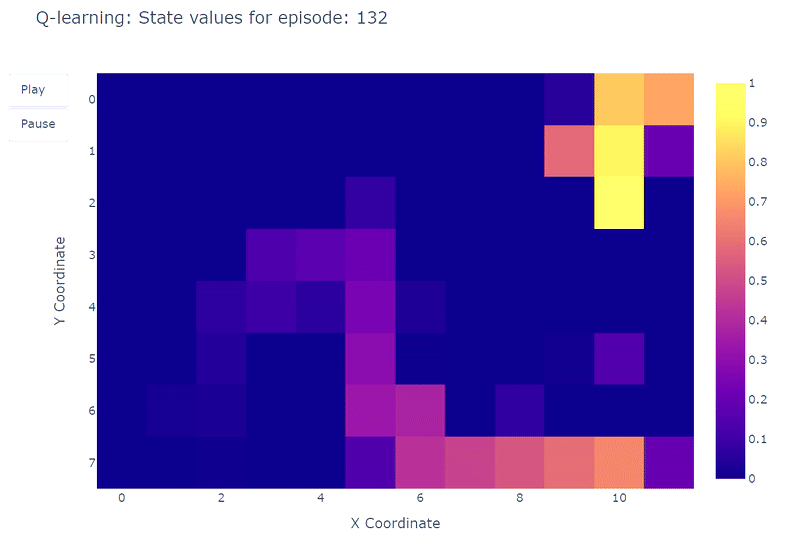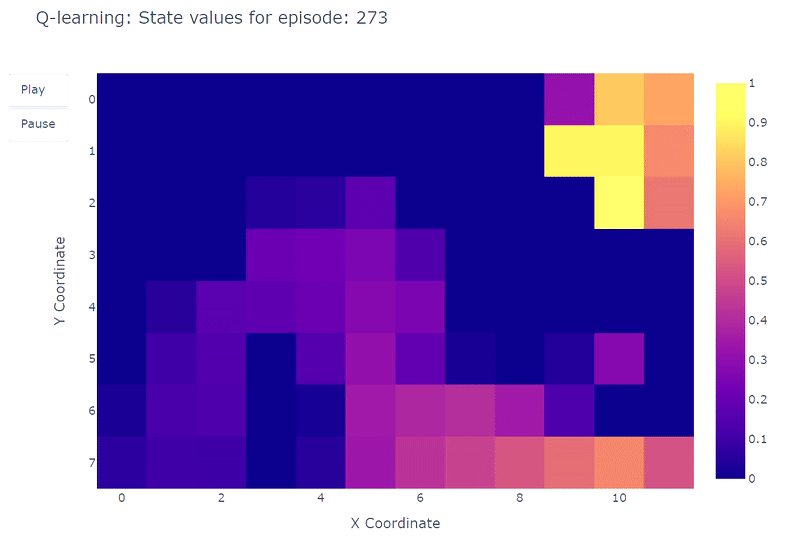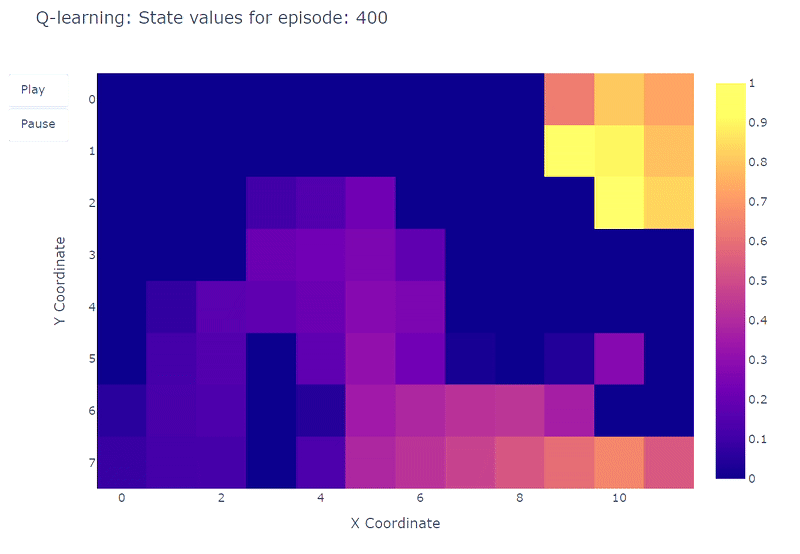
训练期间学习到的每个状态Q值的热力图表示(作者绘制)
在完成400个回合后,对每个单元格的总访问次数进行分析,可以为智能体的平均路线提供一个不错的估计。如下图右侧所示,智能体似乎收敛到了一条次优路线,避开了单元格(4,4)并始终沿着下壁行进。
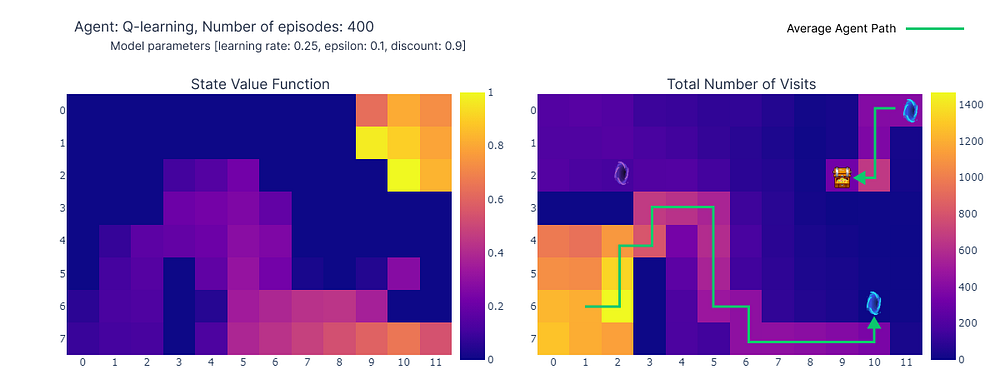
(左) 每个状态最大动作价值的估计,(右) 每个状态的访问次数(作者绘制)
由于这种次优策略,智能体每个回合最少需要21步才能完成,遵循“总访问次数”图中所示的路径。步数的变化可归因于ε-贪婪策略,该策略引入了10%的随机动作概率。在这种策略下,沿着下壁行进是一种不错的策略,可以限制随机动作可能造成的潜在干扰。
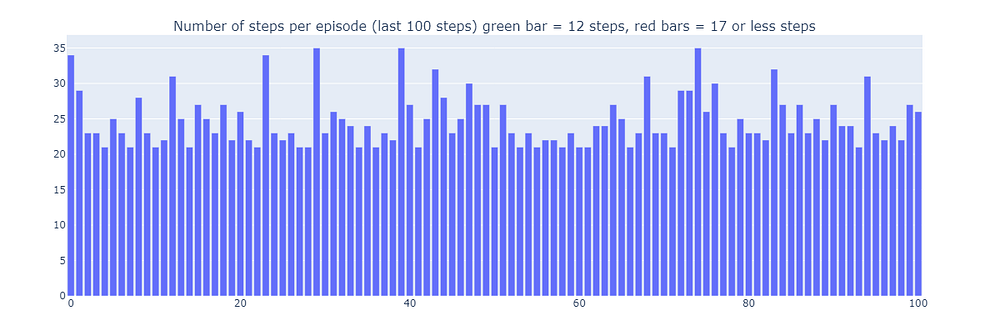
训练最后100个回合(300-400)的步数(作者绘制)
总而言之,Q-learning智能体如前所述,收敛到了一种次优策略。此外,一部分环境仍未被Q函数探索,这使得智能体在第100个回合后紫色传送门出现时,无法找到新的最优路径。
这些性能限制可归因于相对较低的训练步数(400步),这限制了与环境交互的可能性以及由ε-贪婪策略引起的探索程度。
规划是基于模型强化学习方法的一个重要组成部分,对于提高样本效率和动作价值估计特别有用。Dyna-Q和Dyna-Q+就是结合了规划步骤的TD算法的优秀范例。
Dyna-Q算法
Dyna-Q算法(动态Q-learning)是基于模型强化学习与TD学习的结合。
基于模型的强化学习算法依赖于环境模型,将规划作为其更新价值估计的主要方式。相比之下,无模型算法则依赖于直接学习。
“环境模型是智能体可以用来预测环境对其行动将如何响应的任何事物”—《强化学习:导论》。
在本文的语境中,该模型可以被视为转移动力学p(s’, r|s, a)的近似。在此,p根据当前的状态-动作对返回一个单一的下一个状态和奖励对。
在p为随机的环境中,我们将区分分布模型和样本模型,前者返回下一个状态和动作的分布,后者则从估计分布中采样返回一个单一的对。
模型在模拟回合方面特别有用,因此可以通过将真实世界交互替换为规划步骤(即与模拟环境的交互)来训练智能体。
实现Dyna-Q算法的智能体属于规划型智能体,这类智能体结合了直接强化学习和模型学习。它们利用与环境的直接交互来更新其价值函数(如Q-learning),也用于学习环境模型。在每次直接交互后,它们还可以执行规划步骤,利用模拟交互来更新其价值函数。
一个简短的国际象棋例子
想象一下下了一盘精彩的国际象棋。在走出每一步棋后,对手的反应能让玩家评估棋步的质量。这类似于收到一个积极或消极的奖励,使玩家能够“更新”自己的策略。如果一步棋导致了失误,那么在相同的棋局配置下,玩家可能不会再走出它。到目前为止,这与直接强化学习相似。
现在,我们加入规划。想象一下,在玩家的每一步棋之后,当对手思考时,玩家会在脑海中回顾之前走的每一步棋,以重新评估其质量。玩家可能会发现最初忽视的弱点,或者发现某些棋步比想象中更好。这些思考也可能让玩家更新自己的策略。这正是规划的意义所在:在不与真实环境交互的情况下,而是通过该环境的模型来更新价值函数。
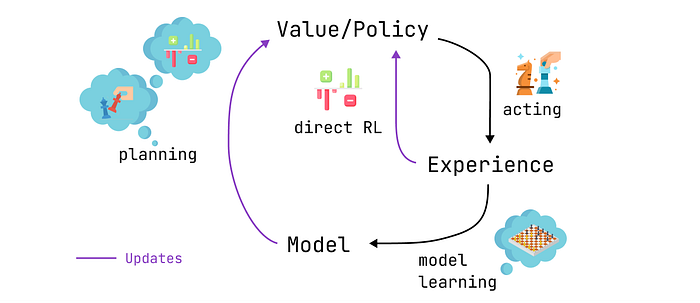
规划型智能体的工作流程:规划、行动、模型学习和直接强化学习(作者绘制)
因此,Dyna-Q相比Q-learning包含了一些额外的步骤:
每次直接更新Q值后,模型会存储观测到的状态-动作对、奖励和下一个状态。此步骤称为模型训练。
- 模型训练后,Dyna-Q会执行n个规划步骤:
- 从模型缓冲区中选择一个随机的状态-动作对(即该状态-动作对在直接交互中被观测到过)。
- 模型生成模拟的奖励和下一个状态。
- 使用模拟观测(s, a, r, s’)更新价值函数。
![Dyna-Q算法的伪代码,摘自《强化学习:导论》[4]](/2025/10/03/d6fe5d09bb50e3ec5f62c3028b88bbd9.png)
Dyna-Q算法的伪代码,摘自《强化学习:导论》[4]
现在,我们使用n=100的Dyna-Q算法复现学习过程。这意味着在每次与环境直接交互后,智能体将使用模型执行100个规划步骤(即更新)。
下面的热力图展示了Dyna-Q模型快速收敛的特点。事实上,该算法仅需大约10个回合就能找到一个最优路径。这得益于每次一步行动都会导致Q值更新101次(而Q-learning只有1次)。
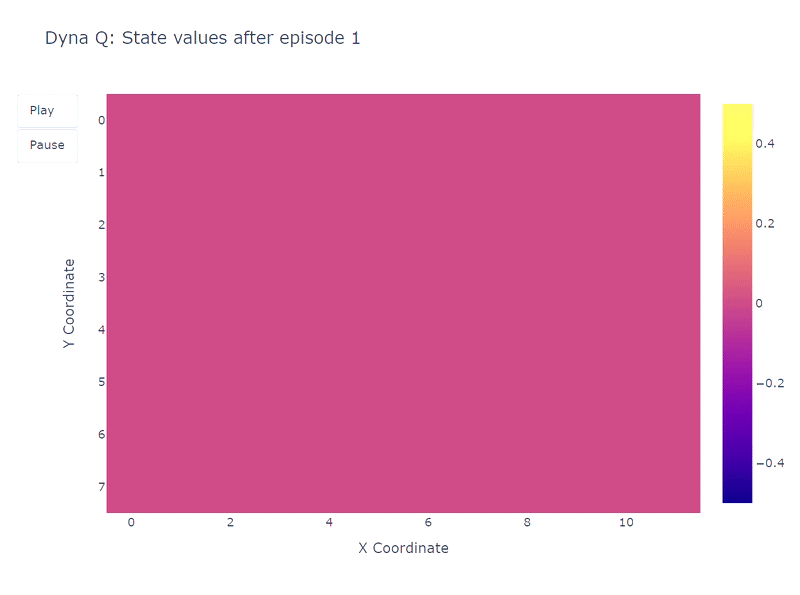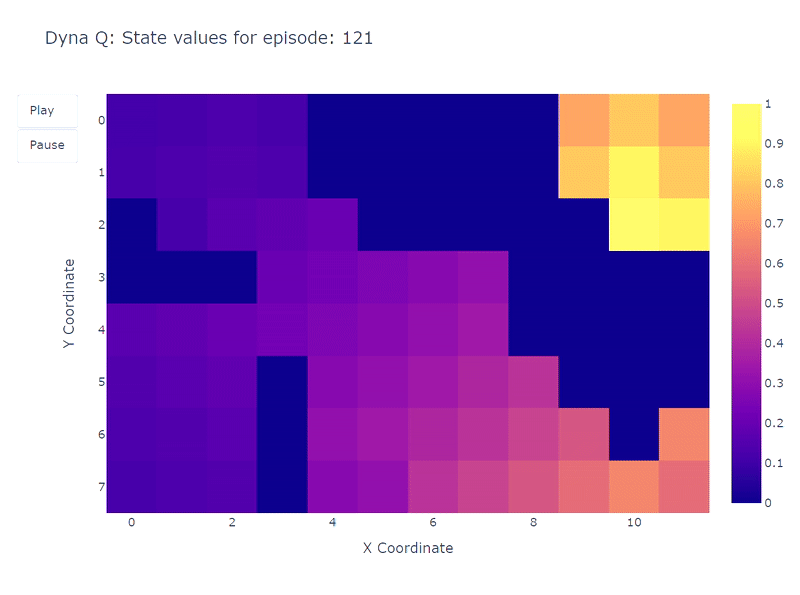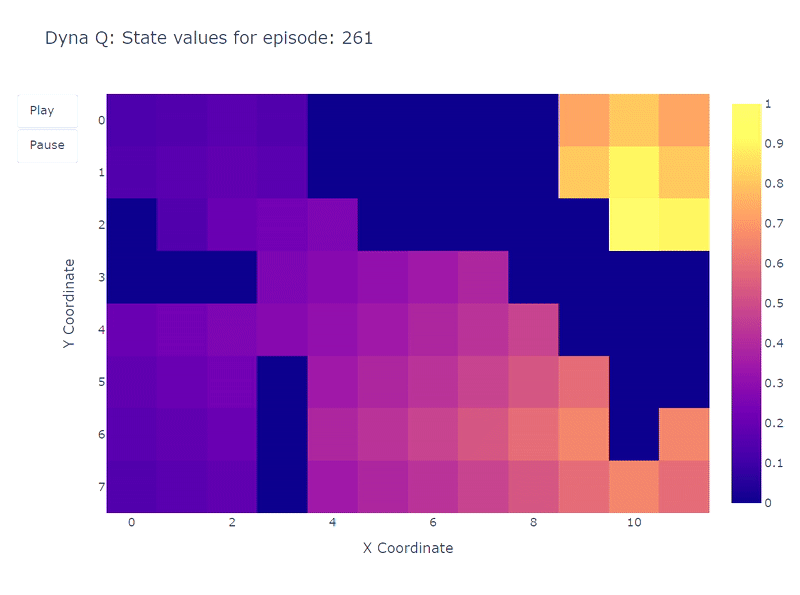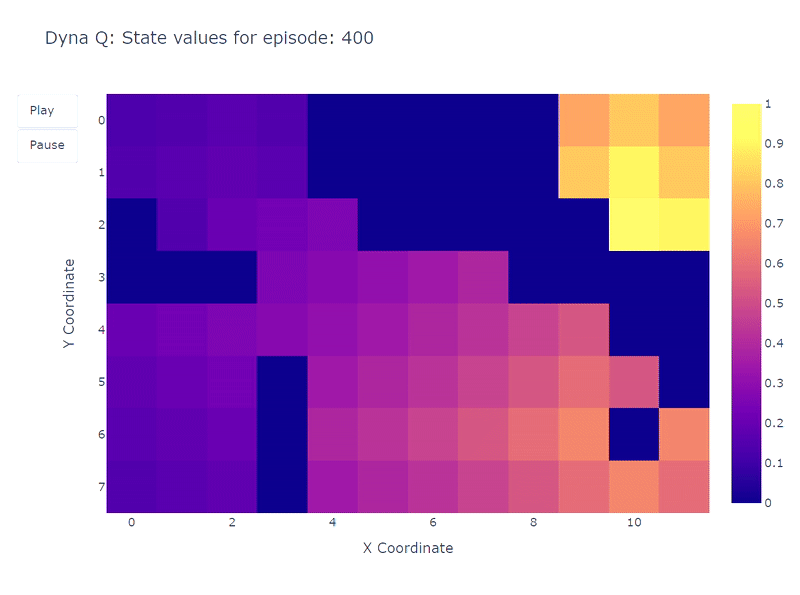
训练期间学习到的每个状态Q值的热力图表示(作者绘制)
规划步骤的另一个好处是能够更好地估计网格中各个位置的动作价值。由于间接更新的目标是模型中存储的随机转移,因此远离目标的状态也能得到更新。
相比之下,在Q-learning中,动作价值是从目标处缓慢传播开来,导致网格映射不完整。
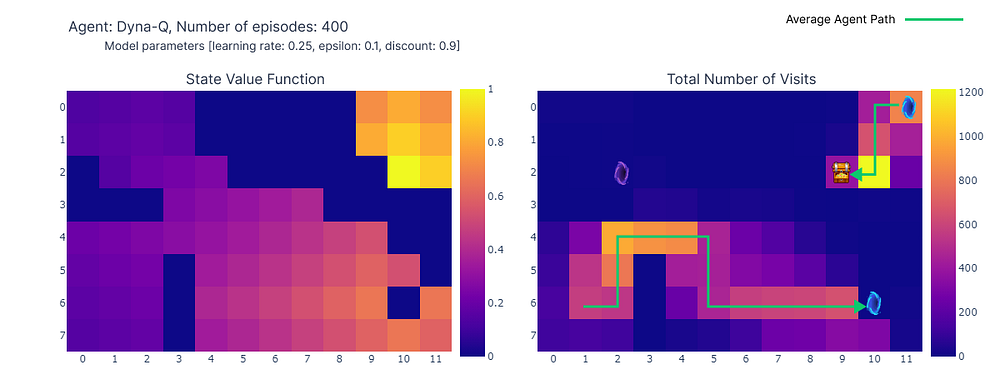
(左) 每个状态最大动作价值的估计,(右) 每个状态的访问次数(作者绘制)
通过使用Dyna-Q,我们找到了一个最优路径,使得网格世界能够在17步内解决,如下图中的红色条所示。尽管偶尔会受到ε-贪婪动作的干扰以进行探索,但最优性能仍能定期实现。
最后,尽管Dyna-Q由于纳入了规划步骤,可能比Q-learning看起来更有说服力,但必须记住,规划引入了计算成本与真实世界探索之间的权衡。
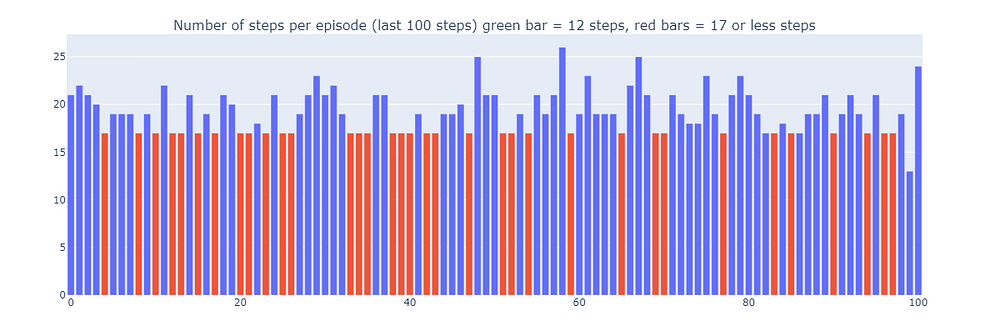
训练最后100个回合(300-400)的步数(作者绘制)
Dyna-Q+算法
到目前为止,无论是Q-learning还是Dyna-Q,都未能找到在第100步后出现的最优路径(紫色传送门)。事实上,这两种算法都迅速收敛到一个最优解,并在训练阶段结束前保持不变。这凸显了在整个训练过程中持续探索的必要性。
Dyna-Q+在很大程度上与Dyna-Q相似,但它对算法做了一个小小的改进。Dyna-Q+持续跟踪每个状态-动作对在与环境真实交互中被尝试以来的时间步数。
具体来说,考虑一个在τ时间步内未被尝试过的、产生奖励r的转移。Dyna-Q+在规划时会假定该转移的奖励是r+κ√τ,其中κ足够小(在本实验中为0.001)。
这种奖励设计上的改变鼓励智能体持续探索环境。它假定一个状态-动作对未被尝试的时间越长,其动力学特性发生变化或模型不准确的可能性就越大。
![Dyna-Q+算法的伪代码,摘自《强化学习:导论》[4]](/2025/10/03/bb1850c7f2f68324fef1a769c79ba342.png)
Dyna-Q+算法的伪代码,摘自《强化学习:导论》[4]
如下图的热力图所示,Dyna-Q+的更新活动远比之前的算法活跃。在第100回合之前,智能体探索了整个网格,找到了蓝色传送门和第一条最优路线。
网格其余部分的动作价值会先下降,然后又缓慢上升,因为左上角的状态-动作对有一段时间未被探索。
一旦紫色传送门在第100回合出现,智能体便找到了新的捷径,整个区域的价值随之上升。直到400个回合完成,智能体将持续更新每个状态-动作对的动作价值,同时保持对网格的偶尔探索。

训练期间学习到的每个状态Q值的热力图表示(作者绘制)
得益于模型奖励中添加的额外奖励,智能体最终获得了Q函数的完整映射(每个状态或单元格都具有动作价值)。
结合持续探索,智能体在新的最优路线(即最优策略)出现时,能够及时发现并利用它,同时保留了之前的解决方案。
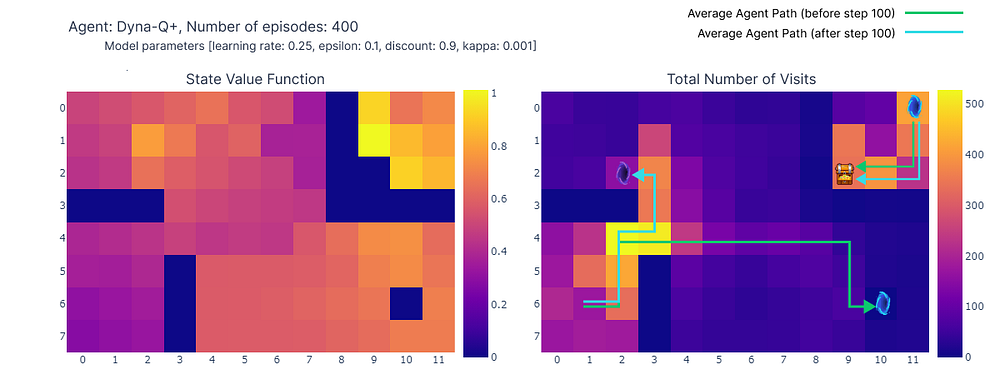
(左) 每个状态最大动作价值的估计,(右) 每个状态的访问次数(作者绘制)
然而,Dyna-Q+中的探索-利用权衡确实伴随着一定的代价。当状态-动作对长时间未被访问时,探索奖励会鼓励智能体重新访问这些状态,这可能会暂时降低其即时性能。这种探索行为优先考虑更新模型以改善长期决策。
这解释了为什么Dyna-Q+的一些回合可能长达70步,而Q-learning和Dyna-Q最长分别为35步和25步。Dyna-Q+中较长的回合反映了智能体愿意投入额外步数进行探索,以收集更多关于环境的信息并完善其模型,即使这会导致短期性能下降。
相比之下,Dyna-Q+能够定期达到(如下图中绿色条所示)之前算法未能实现的最佳性能。
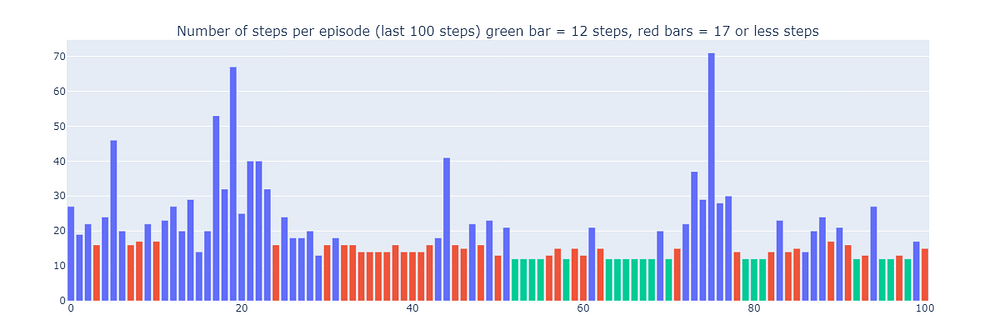
训练最后100个回合(300-400)的步数(作者绘制)
总结与算法比较
为了比较算法之间的关键差异,本文使用了两个指标(请注意,结果取决于输入参数,为简化起见,所有模型均使用相同参数):
- 每个回合的步数:该指标表征了算法收敛到最优解决方案的速度。它也描述了算法在收敛后的行为,特别是在探索方面。
- 平均累积奖励:指成功获得正奖励的回合百分比。
分析每个回合的步数(见下图)揭示了基于模型和无模型方法的几个方面:
- 基于模型的效率:在本次特定的网格世界中(该特性在强化学习中也更普遍地被观察到),基于模型的算法(Dyna-Q和Dyna-Q+)往往具有更高的样本效率。这是因为它们可以利用学习到的环境模型进行预先规划,从而更快地收敛到接近最优或最优解决方案。
- Q-learning的收敛性:Q-learning虽然最终也能收敛到接近最优的解决方案,但需要更多的回合(125个)才能实现。值得强调的是,Q-learning每一步只执行1次更新,这与Dyna-Q和Dyna-Q+执行的多次更新形成对比。
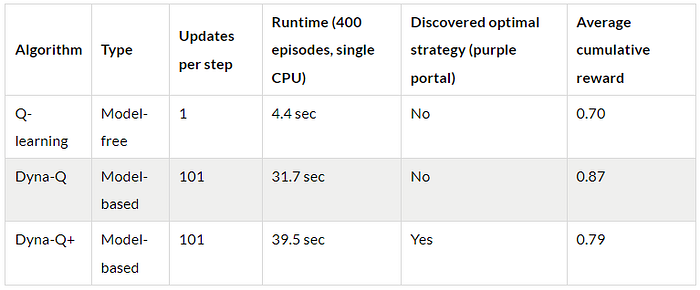
- 多次更新:Dyna-Q和Dyna-Q+每一步执行101次更新,这有助于其更快收敛。然而,这种样本效率的权衡是计算成本(参见下表中的运行时长部分)。
- 复杂环境:在更复杂或随机的环境中,基于模型方法的优势可能会减弱。模型可能引入错误或不准确性,从而导致次优策略。因此,本次比较应被视为不同方法的优缺点概述,而非直接的性能对比。
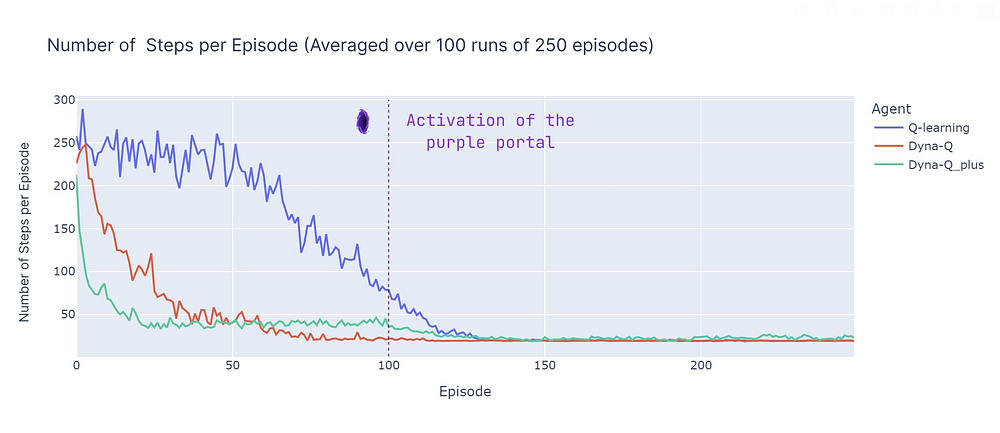
平均100次运行中每个回合步数的比较(作者绘制)
现在我们引入平均累积奖励(ACR),它表示智能体达到目标的回合百分比(因为达到目标的奖励为1,触发陷阱的奖励为0),ACR可简单计算为:
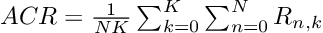
其中,N是回合数(250),K是独立运行次数(100),R n,k是第k次运行中第n个回合的累积奖励。
以下是所有算法的性能细分:
- Dyna-Q收敛迅速,并取得了最高的总回报,ACR达到87%。这意味着它能高效学习并在大部分回合中达到目标。
- Q-learning也达到了相似的性能水平,但需要更多回合才能收敛,这解释了其稍低的ACR,为70%。
- Dyna-Q+迅速找到一个好的策略,在仅15个回合后累积奖励就达到0.8。然而,奖励附加值引起的变异性和探索在第100步之前降低了性能。在100步之后,随着它发现新的最优路径,性能开始提高。但短期探索牺牲了其性能,导致ACR为79%,低于Dyna-Q但高于Q-learning。
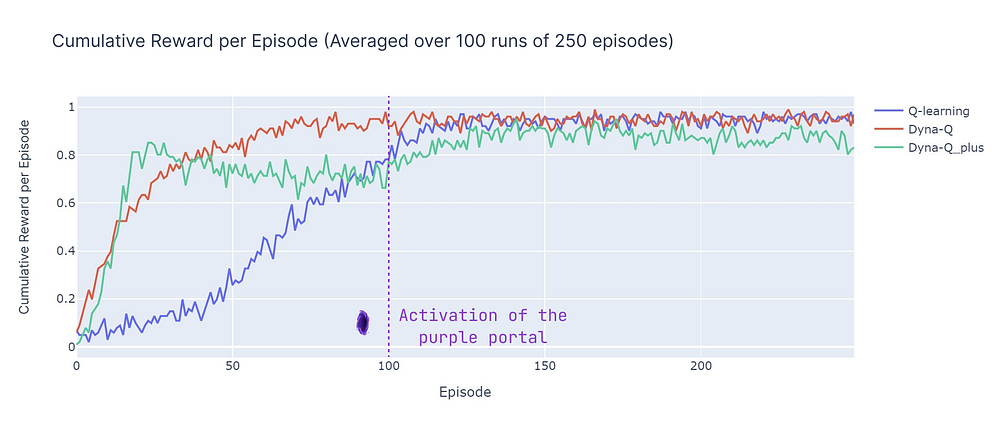
平均100次运行中每个回合累积奖励的比较(作者绘制)
结论
本文介绍了时序差分学习的基本原理,并将Q-learning、Dyna-Q和Dyna-Q+应用于一个定制的网格世界。该网格世界的设计有助于强调持续探索的重要性,以在不断变化的环境中发现和利用新的最优策略。通过比较每个回合的步数和累积奖励等性能指标,展示了这些算法的优缺点。
总而言之,与无模型方法(Q-learning)相比,基于模型的方法(Dyna-Q、Dyna-Q+)受益于更高的样本效率,但代价是计算效率。然而,在随机性更强或更复杂的环境中,模型的不准确性可能会阻碍性能,并导致次优策略。
参考文献:
- [1] Demis Hassabis,AlphaFold揭示蛋白质宇宙结构( 2022), DeepMind
- [2] Elia Kaufmann, Leonard Bauersfeld, Antonio Loquercio, Matthias Müller, Vladlen Koltun &Davide Scaramuzza,使用深度强化学习进行冠军级无人机竞速(2023), Nature
- [3] Nathan Lambert, LouisCastricato, Leandro von Werra, Alex Havrilla,图解人类反馈强化学习 (RLHF), HuggingFace
- [4] Sutton, R. S., & Barto, A. G..强化学习:导论(2018), Cambridge (Mass.): The MIT Press.