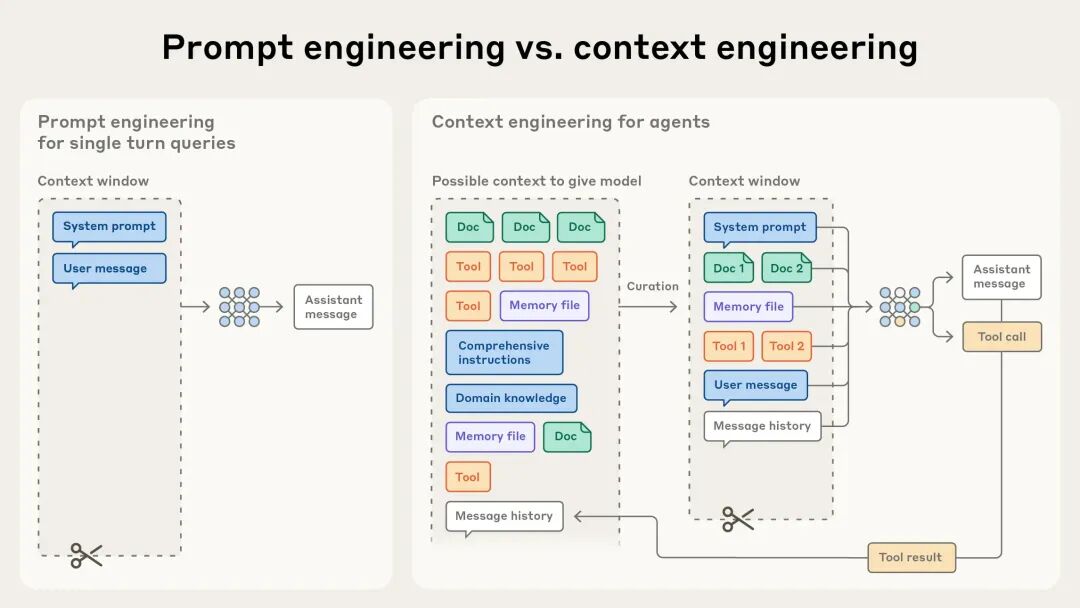
在当下人工智能热潮中，似乎每个人都倾向于使用**视觉-语言模型（Vision-Language Models）**和大型**视觉Transformer模型（Vision Transformers）**来解决计算机视觉领域的各种问题。许多人将这些工具视为万能解决方案，并立即采用最新、最炫的模型，却常常忽略了**理解需要提取的底层信号**的重要性。然而，很多时候，大道至简反而更显其美。工程师们常学到的一课便是：不要将简单问题的解决方案复杂化。
处理流程步骤动画演示
本文将展示如何应用一些简单的经典计算机视觉技术，来检测平面上的矩形对象，并对倾斜的矩形进行透视变换。类似的方法在文档扫描和提取等应用中被广泛使用。
在此过程中，读者将学习到一些有趣的经典计算机视觉概念，包括如何对多边形点进行排序，以及这与组合分配问题之间的关联。
概述
检测
在数独网格检测方面，可以考虑多种方法，从简单的阈值处理、霍夫直线变换或某种形式的边缘检测，到训练深度学习模型进行分割或关键点检测。
为了明确问题范围，此处定义一些假设：
- 数独网格在画面中清晰可见且完整，具有明确的四边形边界，并与背景形成强烈对比。
- 打印数独网格的表面必须是平坦的，但可以从某个角度拍摄，导致其看起来倾斜或旋转。
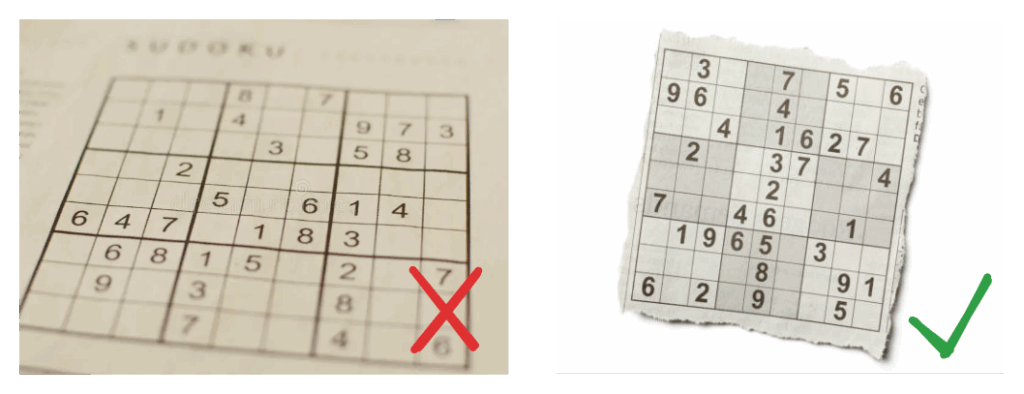
不同图像质量的示例
接下来将展示一个包含一些过滤步骤的简单流程，以检测数独网格的边界。从宏观上看，处理流程如下：
处理流程步骤可视化
灰度处理
在第一步中，只需将输入图像从其三个颜色通道转换为单通道灰度图像，因为在图像处理过程中无需颜色信息。
def find_sudoku_grid(
image: np.ndarray,
) -> np.ndarray | None:
"""
在图像中找到最大的类方形轮廓，可能是数独网格。
返回:
找到的网格轮廓的Numpy数组，如果未找到则返回None。
"""
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
边缘检测
将图像转换为灰度后，可以利用 Canny 边缘检测算法来提取边缘。此算法有两个阈值可供选择，用于确定像素是否被接受为边缘：
Canny 边缘检测的阈值
在检测数独网格的场景中，通常假设网格边框具有非常强的边缘。可以设定较高的上限阈值以抑制噪声出现在掩膜中，同时设置一个不太低的下限阈值，以避免与主边框连接的小噪声边缘被排除。在将图像传递给 Canny 算法之前，通常会使用模糊滤波器来减少噪声，但在本例中，边缘非常强烈但狭窄，因此省略了模糊处理。
def find_sudoku_grid(
image: np.ndarray,
canny_threshold_1: int = 100,
canny_threshold_2: int = 255,
) -> np.ndarray | None:
"""
在图像中找到最大的类方形轮廓，可能是数独网格。
参数:
image: 输入图像。
canny_threshold_1: Canny 边缘检测器的下限阈值。
canny_threshold_2: Canny 边缘检测器的上限阈值。
返回:
找到的网格轮廓的Numpy数组，如果未找到则返回None。
"""
...
canny = cv2.Canny(gray, threshold1=canny_threshold_1, threshold2=canny_threshold_2)
Canny 边缘处理后的掩膜图像
膨胀处理
接着，对边缘检测掩膜进行后处理，使用膨胀核来弥合掩膜中的小间隙。
def find_sudoku_grid(
image: np.ndarray,
canny_threshold_1: int = 100,
canny_threshold_2: int = 255,
morph_kernel_size: int = 3,
) -> np.ndarray | None:
"""
在图像中找到最大的类方形轮廓，可能是数独网格。
参数:
image: 输入图像。
canny_threshold_1: Canny 边缘检测器的第一个阈值。
canny_threshold_2: Canny 边缘检测器的第二个阈值。
morph_kernel_size: 形态学操作核的大小。
返回:
找到的网格轮廓的Numpy数组，如果未找到则返回None。
"""
...
kernel = cv2.getStructuringElement(
shape=cv2.MORPH_RECT, ksize=(morph_kernel_size, morph_kernel_size)
)
mask = cv2.morphologyEx(canny, op=cv2.MORPH_DILATE, kernel=kernel, iterations=1)
膨胀处理后的掩膜图像
轮廓检测
二进制掩膜准备好后，可以运行轮廓检测算法来查找连贯的斑点，并过滤出具有四个点的单个轮廓。
contours, _ = cv2.findContours(
mask, mode=cv2.RETR_EXTERNAL, method=cv2.CHAIN_APPROX_SIMPLE
)
掩膜图像上检测到的轮廓
最初的轮廓检测将返回一个包含组成轮廓的每个像素的轮廓列表。可以利用 Douglas–Peucker 算法迭代地减少轮廓中的点数，并用一个简单的多边形来近似轮廓。可以为算法选择一个点之间的最小距离。
如果假设即使对于一些最倾斜的矩形，其最短边也至少是形状周长的10%，那么可以将轮廓过滤为精确具有四个点的多边形。
contour_candidates: list[np.ndarray] = []
for cnt in contours:
# 将轮廓近似为多边形
epsilon = 0.1 * cv2.arcLength(curve=cnt, closed=True)
approx = cv2.approxPolyDP(curve=cnt, epsilon=epsilon, closed=True)
# 只保留具有4个顶点的多边形
if len(approx) == 4:
contour_candidates.append(approx)
最终选取检测到的最大轮廓，通常认为是最终的数独网格。将轮廓按面积逆序排序，然后取第一个元素，即对应最大轮廓面积的轮廓。
best_contour = sorted(contour_candidates, key=cv2.contourArea, reverse=True)[0]
原始图像上高亮显示的过滤后轮廓
透视变换
最后，需要将检测到的网格变换回其正方形形状。为实现此目的，可以采用透视变换。通过指定数独网格轮廓的四个点最终应放置在图像的四个角的位置，即可计算出变换矩阵。
rect_dst = np.array(
[[0, 0], [width - 1, 0], [width - 1, height - 1], [0, height - 1]],
)
为了将轮廓点与目标角点匹配，这些点需要先进行排序，以便正确分配。此处将角点定义为以下顺序：
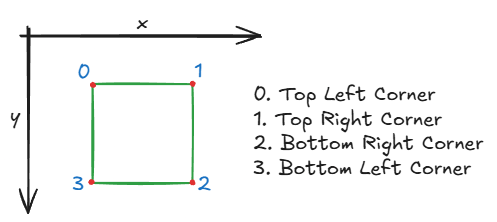
方案A：基于和/差的简单排序
为了对提取的角点进行排序并将其分配给这些目标点，一种简单的算法可以考察每个角点的 x 和 y 坐标的 和（sum） 和 差（differences）。
p_sum = p_x + p_y
p_diff = p_x - p_y
根据这些值，现在可以区分这些角点：
- 左上角具有较小的 x 和 y 值，其和最小
argmin(p_sum)。 - 右下角具有最大的和
argmax(p_sum)。 - 右上角具有最大的差
argmax(p_diff)。 - 左下角具有最小的差
argmin(p_diff)。
在以下动画中，动画演示了旋转正方形的四个角点如何与图像角点进行分配。彩色线条表示每个正方形角点被分配到的相应图像角点。
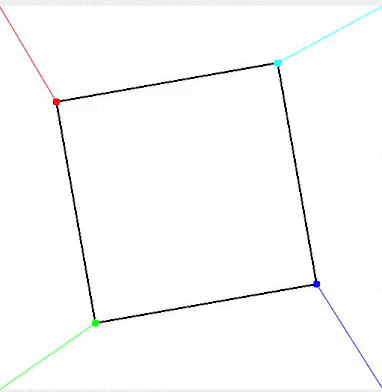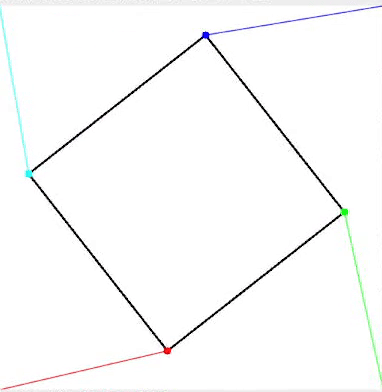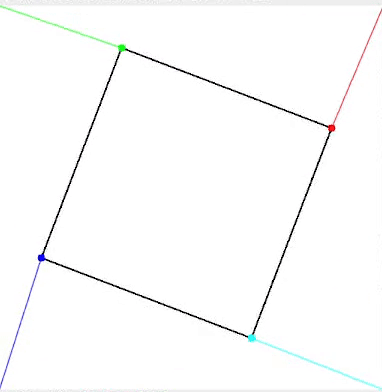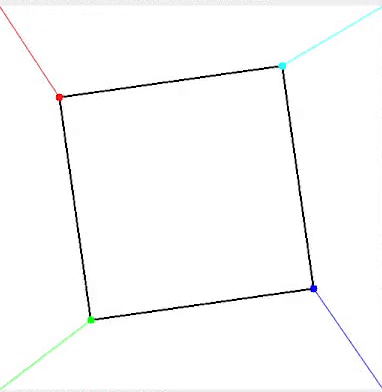
旋转正方形动画，每个角点带有不同颜色和线条指示与图像角点的分配
def order_points(pts: np.ndarray) -> np.ndarray:
"""
以一致的顺序（左上、右上、右下、左下）排列轮廓的四个角点。
参数:
pts: 表示四个角点的Numpy数组，形状为(4, 2)。
返回:
已排序的Numpy数组，形状为(4, 2)。
"""
# 如有需要，将形状从 (4, 1, 2) 重塑为 (4, 2)
pts = pts.reshape(4, 2)
rect = np.zeros((4, 2), dtype=np.float32)
# 左上角点的和最小，而右下角点的和最大
s = pts.sum(axis=1)
rect[0] = pts[np.argmin(s)]
rect[2] = pts[np.argmax(s)]
# 右上角点的差最小，而左下角点的差最大
diff = np.diff(pts, axis=1)
rect[1] = pts[np.argmin(diff)]
rect[3] = pts[np.argmax(diff)]
return rect
除非矩形严重倾斜，否则这种方法效果良好，例如下面的例子。在这种情况下，可以清楚地看到此方法存在缺陷，因为同一个矩形角点被分配给了多个图像角点。
相同的分配过程在倾斜旋转的四边形上失败
方案B：分配优化问题
另一种方法是最小化每个点与其分配角点之间的距离。这可以通过计算每个点与角点之间的 pairwise_distances 以及使用 scipy 库中的 linear_sum_assignment 函数来实现，该函数在最小化成本函数的同时解决分配问题。
def order_points_simplified(pts: np.ndarray) -> np.ndarray:
"""
对一组点进行排序，使其与目标角点集最佳匹配。
参数:
pts: 表示要排序的点的Numpy数组，形状为(N, 2)。
返回:
已排序的Numpy数组，形状为(N, 2)。
"""
# 如有需要，将形状从 (N, 1, 2) 重塑为 (N, 2)
pts = pts.reshape(-1, 2)
# 计算每个点与每个目标角点之间的距离
D = pairwise_distances(pts, pts_corner)
# 找到最优的一对一分配
# row_ind[i] 应与 col_ind[i] 匹配
row_ind, col_ind = linear_sum_assignment(D)
# 创建一个空数组来保存排序后的点
ordered_pts = np.zeros_like(pts)
# 根据匹配到的角点，将每个点放置到正确的槽位中。
# 例如，与 target_corners[0] 匹配的点放置到 ordered_pts[0] 中。
ordered_pts[col_ind] = pts[row_ind]
return ordered_pts
倾斜旋转四边形动画，角点正确分配到图像角点
尽管此解决方案有效，但它并非理想选择，因为它依赖于形状点与角点之间的图像距离，并且由于必须构建距离矩阵，计算成本更高。当然，在分配四个点的情况下，这可以忽略不计，但此解决方案不适用于具有许多点的多边形！
方案C：带锚点的循环排序
第三种方案是一种非常轻量级且高效的排序和分配形状点到图像角点的方法。其核心思想是根据形心位置为形状的每个点计算一个角度。
每个角点分配角度的示意图
由于角度是循环的，需要选择一个锚点以保证点的绝对顺序。此处简单地选择 x 和 y 坐标之和最小的点作为锚点。
def order_points(self, pts: np.ndarray) -> np.ndarray:
"""
按绕形心的角度对点进行排序，然后旋转以从左上角开始。
参数:
pts: 形状为(4, 2)的Numpy数组。
返回:
已排序的Numpy数组，形状为(4, 2)。"""
pts = pts.reshape(4, 2)
center = pts.mean(axis=0)
angles = np.arctan2(pts[:, 1] - center[1], pts[:, 0] - center[0])
pts_cyclic = pts[np.argsort(angles)]
sum_of_coords = pts_cyclic.sum(axis=1)
top_left_idx = np.argmin(sum_of_coords)
return np.roll(pts_cyclic, -top_left_idx, axis=0)
倾斜旋转四边形动画，角点使用角度分配方法正确分配
现在可以利用此函数对轮廓点进行排序：
rect_src = order_points(grid_contour)
应用透视变换
当确定了点与目标位置的对应关系后，便可着手进行最有趣的部分：创建并实际将透视变换应用于图像。
应用透视变换动画
由于已获得排序后的检测到的四边形点列表 rect_src，以及目标角点 rect_dst，可以利用 OpenCV 方法计算变换矩阵：
warp_mat = cv2.getPerspectiveTransform(rect_src, rect_dst)结果是一个 3×3 的变换矩阵，它定义了如何从倾斜的3D透视视图转换为2D平面俯视图。为了获得数独网格的这种平面俯视图，可以将此透视变换应用于原始图像：
warped = cv2.warpPerspective(img, warp_mat, (side_len, side_len))至此，一个完美的正方形数独网格便呈现在眼前！
透视变换后数独网格的最终平面俯视图
结论
本文介绍了一个简单的流程，利用经典计算机视觉技术从图片中提取数独网格。这些方法提供了一种简单有效的方式来检测数独网格的边界。当然，由于其简单性，这种方法在泛化到不同设置和极端环境（如弱光或强阴影）时存在一定的局限性。如果检测需要泛化到大量不同的场景，采用基于深度学习的方法可能更为合适。
接下来，使用透视变换获得网格的平面俯视图。这张图像现在可以用于进一步处理，例如提取网格中的数字并实际解决数独。在下一篇文章中，将深入探讨这些自然而然的后续步骤。
