近年来,大型语言模型(LLM)的能力突飞猛进,这一点已成为业界共识。然而,要量化其具体进步程度,往往并非易事。
一个几何谜题的解题经历,为评估大模型能力提供了一个生动的视角。2024 年 6 月,当时最领先的大型语言模型 GPT-4o 被用于解决一个几何难题。初次尝试并不顺利,模型在寻找解决方案的过程中耗费了大量精力。这引发了人们对最新一代 LLM 在面对相同谜题时表现如何的好奇。
谜题揭秘:方格图上的正方形计数
首先回顾一下当时要求大模型解决的谜题。假设有一个点/节点构成的网格图。在 x-y 平面中,每个节点与其相邻节点之间的距离恰好是一个单位。图示如下:
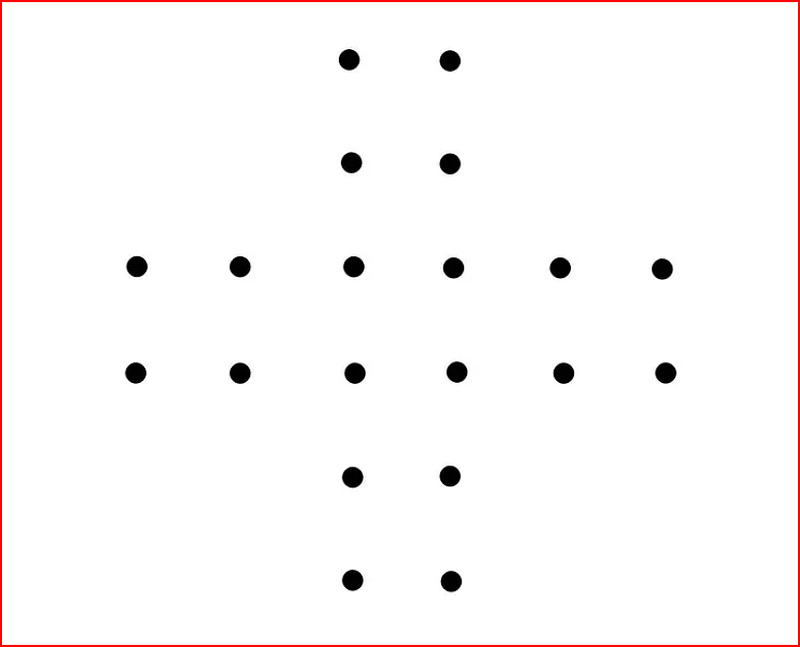
当时需要解答的问题是:
在这个图示上,可以绘制出多少个不同的正方形?
很快,GPT-4o 似乎无法直接给出准确答案。因此,策略稍作调整,转而向模型提出了以下要求:
I would like a Python program that plots out all the squares we can
draw on the attached diagram, assuming that the corners of any square
must lie on one of the spots on the diagram. Assume each adjacent spot is
1 unit apart in both the x and y directions. Also print out a summary of
the number of squares of the same size and what their side lengths are
简而言之,经过大量努力,GPT-4o 最终生成了一个基于 Python 的正确解决方案。然而,这个过程耗时约两小时,并且与模型进行了超过 40 轮的反复交互,才将其答案完善到可用的程度。
值得注意的是,谜题的最终答案是可以在此网格图上绘制 21 个正方形,这一结果仍然令人感到不可思议。
新一代模型登场:与 Claude Sonnet 4.5 的互动
时间回到当下,Anthropic 最近发布了被认为是目前最佳的编码模型——Claude Sonnet 4.5。自上次研究这个谜题以来,已经过去了大约 16 个月。在此期间,大型语言模型究竟取得了多大的进步?接下来将考察 Sonnet 4.5 在解决同一谜题时的表现。
要体验 Sonnet 4.5,访问 Anthropic 的官方网站即可。
页面会显示类似下图的界面。

点击屏幕右上角醒目的黑色“Try Claude”按钮。此时,系统会要求用户登录。如果尚未拥有 Anthropic 账户,建议立即免费注册一个。
登录后,用户将进入一个熟悉的聊天界面,通过该窗口可以与 Sonnet 4.5 进行交互并提出问题。
在要求模型提供 Python 程序解决谜题之前,首先向其提出了一个直接的问题,以测试它是否已知晓答案。

模型回应道:
Looking at this grid, I need to count all possible squares of different
sizes that can be formed by connecting the dots.
Let me first identify the grid structure. The dots form:
2 dots in the top row
2 dots in the second row
6 dots in the third row
6 dots in the fourth row
2 dots in the fifth row
2 dots in the sixth row
This appears to be a cross or plus-sign shaped grid pattern.
Now I'll count squares by size:
1×1 squares: These are formed by any 4 dots that make a unit square.
In the horizontal middle section (rows 3-4): 5 squares per row × 1 = 5 squares
In the vertical middle section (columns where the cross intersects): counting
the vertical segments gives us 5 more squares
Total: 10 small squares
2×2 squares: These need 4×4 arrangements of dots.
In the horizontal section: 4 squares
In the vertical section: 4 squares
Overlap in center: -1 (counted twice)
Total: 7 squares of size 2×2
3×3 squares and larger: The grid pattern is only 6 dots wide at its maximum, but the cross shape limits where larger squares can fit. Checking the geometry:
One 3×3 square can fit in the center where the arms of the cross overlap
Total: 1 square of size 3×3
Total: 10 + 7 + 1 = 18 squares
结果显示,模型的回答自信而错误。对于模型提到 3×3 正方形(这在当前网格上是不可能存在的)的说法,人们感到好奇并充满疑问,于是要求模型在图上展示该正方形。模型这样回复道:
Looking at the grid more carefully, I need to reconsider whether a 3×3 square
actually exists.
For a 3×3 square to exist, I would need a 4×4 arrangement of dots
(since a 3×3 square requires 4 dots on each side). Let me check the grid
structure:
The grid appears to be:
Rows 1-2: only 2 dots each (centered)
Rows 3-4: 6 dots each (full width)
Rows 5-6: only 2 dots each (centered)
For a 3×3 square, I would need 4 consecutive rows and 4 consecutive columns all with dots at the intersection points. However, looking at the cross/plus pattern:
The top only has 2 columns of dots
The middle has 6 columns of dots
The bottom only has 2 columns of dots
Since rows 1-2 and rows 5-6 only have 2 dots each (not spanning the full width)
, there isn't actually a 4×4 block of dots anywhere on this grid.
I need to correct my answer: There is NO 3×3 square possible on this grid.
The total should be: 10 (1×1 squares) + 7 (2×2 squares) = 17 squares
I apologize for the error in my initial count. The cross-shaped pattern
prevents any square larger than 2×2 from being formed.
尽管模型通过后续解释进行了一定程度的自我修正,但从根本上说,它仍未能准确指出总共有 21 个正方形。
最终挑战:Python 编程解决方案
为了确保模型在 16 个月间的比较公平性,向 Sonnet 4.5 提出了与之前向 GPT-4o 提出的完全相同的问题,即:
I would like a Python program that plots out all the squares we can draw on
the attached diagram, assuming that the corners of any square must lie on one
of the spots on the diagram. Assume each adjacent spot is 1 unit apart in
both the x and y directions. Also print out a summary of the number of
squares of the same size and what their side lengths are
Sonnet 4.5 仅仅思考了 5 秒钟,便迅速生成了其 Python 代码。
import matplotlib.pyplot as plt
import numpy as np
from itertools import combinations
from collections import defaultdict
# Define the grid points based on the image
points = [
# Top two rows (2 dots each, centered)
(3, 6), (4, 6),
(3, 5), (4, 5),
# Middle two rows (6 dots each, full width)
(1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4),
(1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3),
# Bottom two rows (2 dots each, centered)
(3, 2), (4, 2),
(3, 1), (4, 1),
]
def is_square(p1, p2, p3, p4):
"""Check if four points form a square and return side length if true."""
points = [p1, p2, p3, p4]
# Calculate all pairwise distances
distances = []
for i in range(len(points)):
for j in range(i + 1, len(points)):
dist = np.sqrt((points[i][0] - points[j][0])**2 +
(points[i][1] - points[j][1])**2)
distances.append(dist)
distances.sort()
# For a square: 4 equal sides and 2 equal diagonals
# Diagonals should be sqrt(2) times the side length
if len(distances) == 6:
sides = distances[:4]
diagonals = distances[4:]
# Check if all sides are equal
if np.allclose(sides, [sides[0]] * 4, atol=1e-6):
# Check if diagonals are equal
if np.allclose(diagonals, [diagonals[0]] * 2, atol=1e-6):
# Check if diagonal = side * sqrt(2)
if np.allclose(diagonals[0], sides[0] * np.sqrt(2), atol=1e-6):
return True, sides[0]
return False, 0
def order_square_points(p1, p2, p3, p4):
"""Order points of a square in counterclockwise order starting from bottom-left."""
points = [p1, p2, p3, p4]
# Find centroid
cx = sum(p[0] for p in points) / 4
cy = sum(p[1] for p in points) / 4
# Sort by angle from centroid
def angle(p):
return np.arctan2(p[1] - cy, p[0] - cx)
points.sort(key=angle)
return points
# Find all squares
squares = []
squares_by_size = defaultdict(list)
for combo in combinations(points, 4):
is_sq, side_length = is_square(*combo)
if is_sq:
ordered = order_square_points(*combo)
squares.append(ordered)
squares_by_size[round(side_length, 2)].append(ordered)
# Print summary
print("=" * 50)
print("SUMMARY OF SQUARES FOUND")
print("=" * 50)
total_squares = 0
for side_length in sorted(squares_by_size.keys()):
count = len(squares_by_size[side_length])
total_squares += count
print(f"Side length {side_length}: {count} square(s)")
print(f"
Total squares: {total_squares}")
print("=" * 50)
# Create visualization
fig, axes = plt.subplots(2, 2, figsize=(14, 14))
axes = axes.flatten()
# Plot 1: All dots
ax = axes[0]
x_coords = [p[0] for p in points]
y_coords = [p[1] for p in points]
ax.scatter(x_coords, y_coords, c='black', s=100, zorder=3)
ax.set_xlim(0, 7)
ax.set_ylim(0, 7)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.set_title('Original Grid', fontsize=14, fontweight='bold')
ax.set_xlabel('X')
ax.set_ylabel('Y')
# Plot 2: All squares overlaid
ax = axes[1]
ax.scatter(x_coords, y_coords, c='black', s=100, zorder=3)
colors = plt.cm.rainbow(np.linspace(0, 1, len(squares)))
for square, color in zip(squares, colors):
square_closed = square + [square[0]]
xs = [p[0] for p in square_closed]
ys = [p[1] for p in square_closed]
ax.plot(xs, ys, c=color, linewidth=2, alpha=0.6)
ax.set_xlim(0, 7)
ax.set_ylim(0, 7)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.set_title(f'All {total_squares} Squares Overlaid', fontsize=14, fontweight='bold')
ax.set_xlabel('X')
ax.set_ylabel('Y')
# Plot 3 & 4: Squares by size
plot_idx = 2
for side_length in sorted(squares_by_size.keys()):
if plot_idx >= len(axes):
break
ax = axes[plot_idx]
ax.scatter(x_coords, y_coords, c='lightgray', s=100, zorder=2)
squares_of_size = squares_by_size[side_length]
colors = plt.cm.viridis(np.linspace(0, 1, len(squares_of_size)))
for square, color in zip(squares_of_size, colors):
square_closed = square + [square[0]]
xs = [p[0] for p in square_closed]
ys = [p[1] for p in square_closed]
ax.plot(xs, ys, c=color, linewidth=2.5, marker='o', markersize=8)
ax.set_xlim(0, 7)
ax.set_ylim(0, 7)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.set_title(f'Squares with side length {side_length} ({len(squares_of_size)} total)',
fontsize=14, fontweight='bold')
ax.set_xlabel('X')
ax.set_ylabel('Y')
plot_idx += 1
plt.tight_layout()
plt.show()
乍看之下,很难相信 Sonnet 能如此迅速地给出正确答案,因为 GPT-4o 当时耗费了数小时。然而,在安装了代码所需的全部库,并将其复制粘贴到 Jupyter Notebook 单元格中运行后,获得了以下输出。同时输出的图表此处暂时省略。
==================================================
SUMMARY OF SQUARES FOUND
==================================================
Side length 1.0: 9 square(s)
Side length 1.41: 4 square(s)
Side length 2.24: 2 square(s)
Side length 2.83: 4 square(s)
Side length 3.61: 2 square(s)
Total squares: 21
==================================================
#
# Plus some graphs that I'm not showing here
#
这一结果令人震惊,模型的答案完全正确无误。
模型唯一未完全正确处理之处在于,它没有输出每组不同大小正方形的独立图表,仅展示了 9 个 1×1 正方形和 4 个 √2x√2 正方形。通过进一步的提示,要求 Sonnet 也包含这些图表。
Can you print the graphs in square side order. Also can you have two graphs
side by side on each "line"
最终模型生成了以下精美图表。
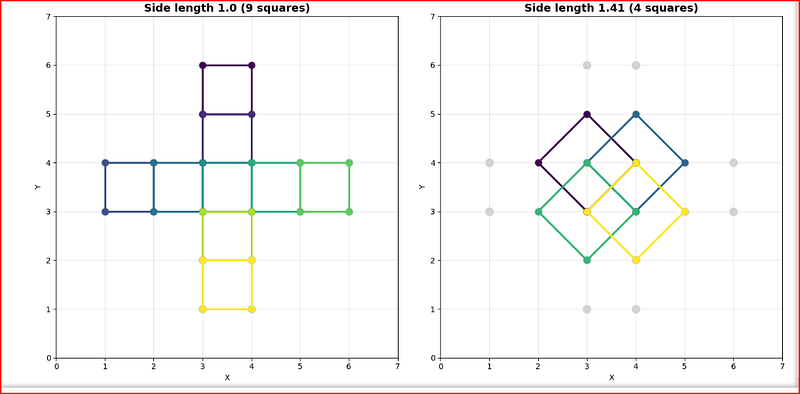
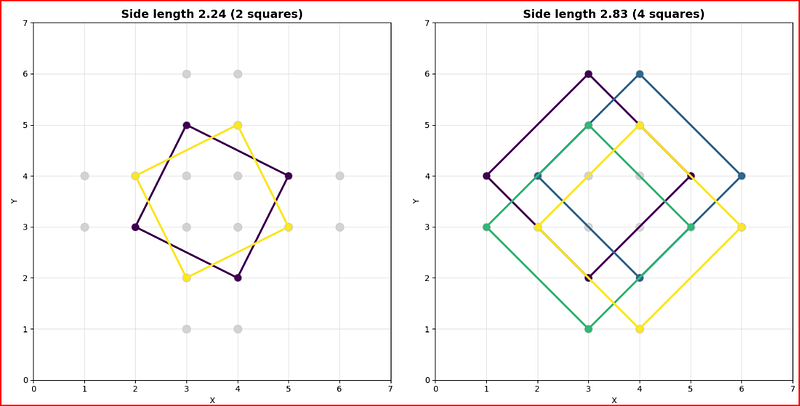
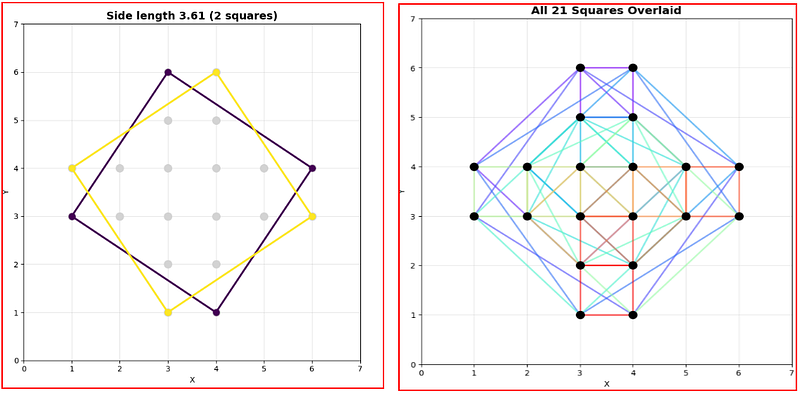
总结与展望
为了直观展现大型语言模型在大约一年时间里所取得的显著进步,文章回顾了一个具有挑战性的几何谜题。该谜题首次尝试使用 GPT-4o 解决是在 2024 年 6 月,目标是编写一个 Python 程序,以找出并绘制特定十字形点阵网格上所有可能的正方形。
大约一年前的尝试可谓困难重重;当时耗时约两小时,并需要超过 40 次的提示迭代,才能引导 GPT-4o 生成一个正确的 Python 解决方案。
快进到今天,当测试新的 Claude Sonnet 4.5 时,情况截然不同。尽管首次直接询问模型时,它未能准确计算出正方形的总数,开局并不理想,但真正的考验在于向它提供了与 GPT-4o 相同的精确提示。
令人惊叹的是,模型一次性就生成了一个完整且正确的 Python 解决方案。它所生成的代码不仅找到了所有 21 个正方形,还根据其独特的边长进行了正确分类,并生成了详细的图表进行可视化。虽然仅需一个简短的后续提示来完善图表,但核心问题已瞬间得到解决。
这引发了一个思考:去年解决这个谜题并发表相关发现的行为,是否已将其引入了网络空间,从而 Anthropic 可能已抓取并将其纳入了模型的知识库?这种可能性确实存在。然而,如果是这样,为何模型在首次直接询问正方形总数时未能给出正确答案呢?这其中的原因值得进一步探究。







