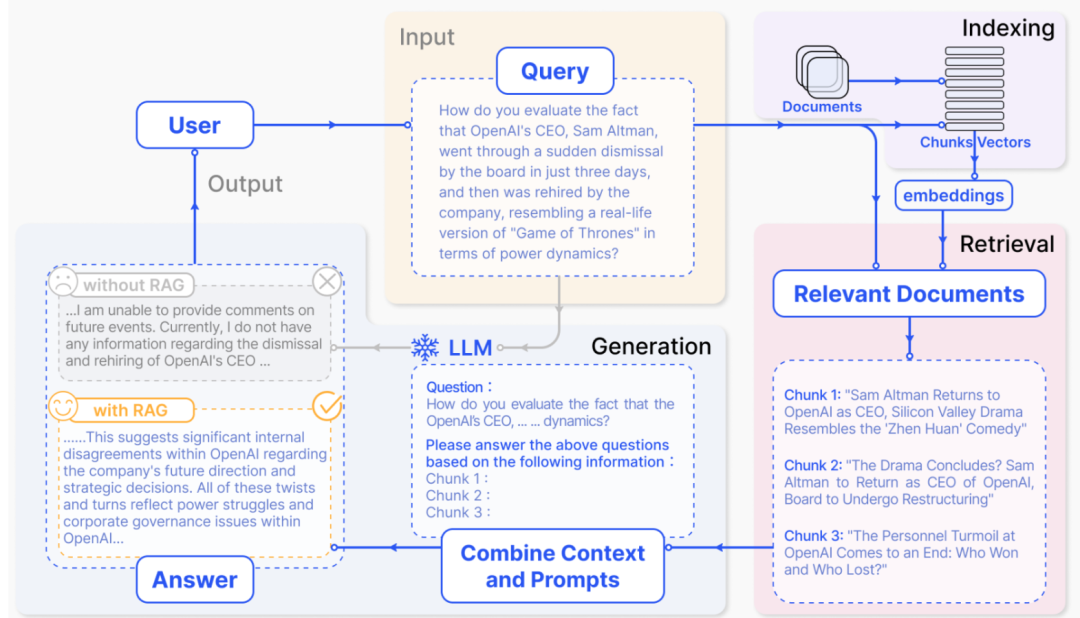
在产品管理过程中,确保产品按预期运行并保持流畅至关重要。通常,我们会依赖关键指标(metrics)来衡量产品的健康状况。许多因素都可能影响这些关键绩效指标(KPIs),无论是内部变动,例如用户界面更新、定价调整或突发事件,还是外部因素,如竞争对手的行动或季节性趋势。因此,持续监控KPIs变得尤为重要,以便在出现异常时能够迅速响应。否则,可能需要数周时间才能发现产品对5%的客户完全失效,或者在最新版本发布后转化率下降了10个百分点。
为了获得这种可见性,可以创建包含关键指标的仪表盘。然而,坦白地说,如果这些仪表盘没有人主动监控,其价值便微乎其微。这就需要两种解决方案:要么安排人员持续关注数十乃至数百个指标,要么构建一个自动化的告警和监控系统。显然,后者是更受推崇的方案。本文将深入探讨一种实用的方法,旨在帮助读者构建一个高效的KPI监控系统。通过本文,读者将了解不同的监控方法,如何搭建第一个统计监控系统,以及在将其部署到生产环境时可能遇到的挑战。
构建监控系统
在深入探讨技术细节之前,首先从宏观层面审视如何构建监控系统架构。在建立监控时,需要做出以下几个关键决策:
- 灵敏度:需要找到一个合适的平衡点,既不能错过重要的异常情况(假阴性),又不能被每天上百次的虚假告警轰炸(假阳性)。稍后将讨论如何调整这些杠杆。
- 维度:选择监控的细分维度也会影响系统的灵敏度。如果某个小细分(例如特定浏览器或国家)出现问题,直接监控该细分的指标会更容易捕捉到问题。但需要注意的是,监控的细分维度越多,面临的假阳性告警也会越多,因此需要找到一个最佳平衡点。
- 时间粒度:如果拥有大量数据且无法承受延迟,那么查看逐分钟的数据可能很有价值。如果数据量不足,可以将其聚合为5-15分钟的桶状数据进行监控。无论哪种方式,除了实时监控之外,通常还需要进行更高层次的每日、每周或每月监控,以关注长期趋势。
然而,监控并不仅仅是技术解决方案。它还关乎所建立的流程:
- 需要有人负责监控和响应告警。在过去的团队中,通过轮值制度来处理这个问题,每周由一人负责审查所有告警。
- 除了自动化监控,进行一些手动检查也很有价值。可以在办公室设置电视显示屏,或者至少建立一个流程,由专人(如轮值人员)每天或每周审查一次指标。
- 需要建立反馈循环。在审查告警并回顾可能错过的事件时,花时间微调监控系统的设置。
- 变更日志(记录所有影响KPIs的变更)的价值不可低估。它能帮助团队始终了解KPIs何时发生了什么变化。此外,它还提供了一个有价值的数据集,用于评估在进行变更时对监控系统的实际影响(例如,新的设置能捕捉到过去多少百分比的异常)。
现在,我们已经了解了宏观层面,接下来深入探讨如何实际检测时间序列数据中的异常的技术细节。
监控框架
有许多现成的框架可用于监控。可以将它们分为两大类。
第一类涉及创建带有置信区间的预测。以下是一些选项:
- 可以使用statsmodels及其对ARIMA类模型的经典实现进行时间序列预测。
- 另一个通常开箱即用且表现良好的选项是Meta的Prophet。它是一个简单的加性模型,能够返回不确定性区间。
- 此外还有GluonTS,一个来自AWS的基于深度学习的预测框架。
第二类专注于异常检测,以下是一些流行的库:
- PyOD:最流行的Python异常值/异常检测工具箱,包含50多种算法(包括时间序列和深度学习方法)。
- ADTK(Anomaly Detection Toolkit):专为无监督/基于规则的时间序列异常检测而构建,易于集成到pandas数据框中。
- Merlion:结合了经典和机器学习方法,用于时间序列的预测和异常检测。
这里只提及了几个示例;市面上还有更多库。当然可以尝试将它们应用于自己的数据,并观察其性能。然而,本文希望分享一种更简单的监控方法,这通常也是起始的选择。尽管它简单到只需一条SQL查询即可实现,但在许多情况下却表现出惊人的效果。这种简单性的另一个显著优势是,几乎可以在任何工具中实现它,而部署更复杂的机器学习方法在某些系统中可能颇具挑战。
监控的统计学方法
监控的核心思想非常直接:利用历史数据建立一个置信区间(CI),并检测当前指标何时超出预期行为范围。通过过去数据的均值和标准差来估算这个置信区间。这只是基本的统计学原理。
置信区间 = (均值 – coef 1 × 标准差 , 均值 + coef 2 × 标准差)
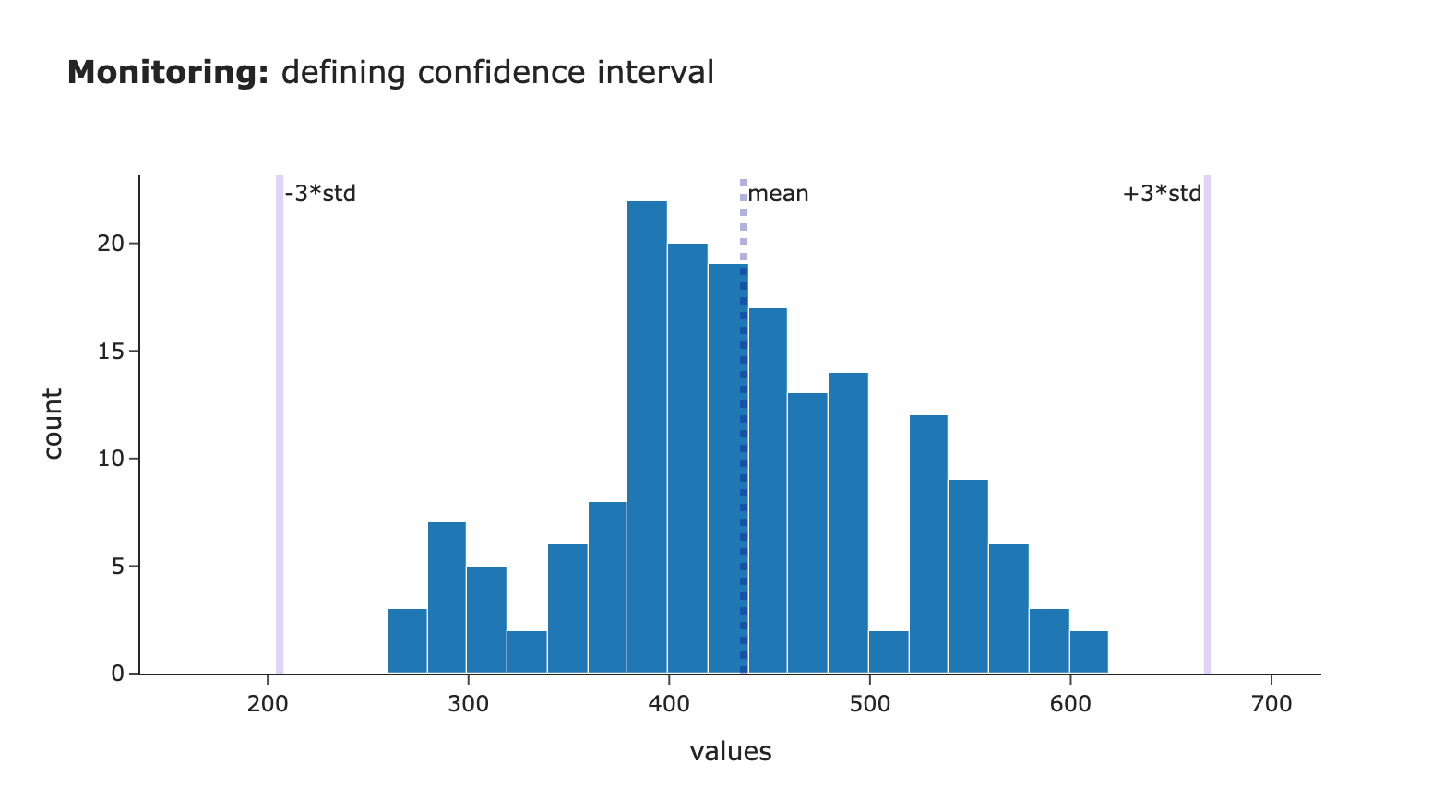
图片作者提供
然而,这种方法的有效性取决于几个关键参数,所做的选择将显著影响告警的准确性。
第一个决策是如何定义用于计算统计数据的数据样本。通常,我们将当前指标与前几天同一时间段的数据进行比较。这涉及两个主要组成部分:
- 时间窗口:通常会围绕当前时间戳取±10-30分钟的窗口,以考虑短期波动。
- 历史天数:偏好使用过去3-5周的同一工作日数据。这种方法考虑了业务数据中通常存在的周度季节性。然而,根据具体的季节性模式,可能会选择不同的方法(例如,将日期分为工作日和周末两组)。
另一个重要参数是用于设定置信区间宽度的系数选择。通常使用三个标准差,因为对于接近正态分布的数据,它覆盖了99.7%的观测值。
正如所见,需要做出几个决策,并且没有一刀切的答案。确定最佳设置最可靠的方法是使用自己的数据进行不同配置的实验,并选择最适合特定用例的配置。因此,现在是时候将这种方法付诸实践,看看它在真实数据上的表现如何。
示例:监控出租车乘车次数
为了验证这一点,我们将使用流行的纽约市出租车数据数据集。加载了2025年5月至7月的数据,并重点关注高容量网约车相关的乘车记录。由于每分钟有数百次行程,我们可以使用逐分钟的数据进行监控。
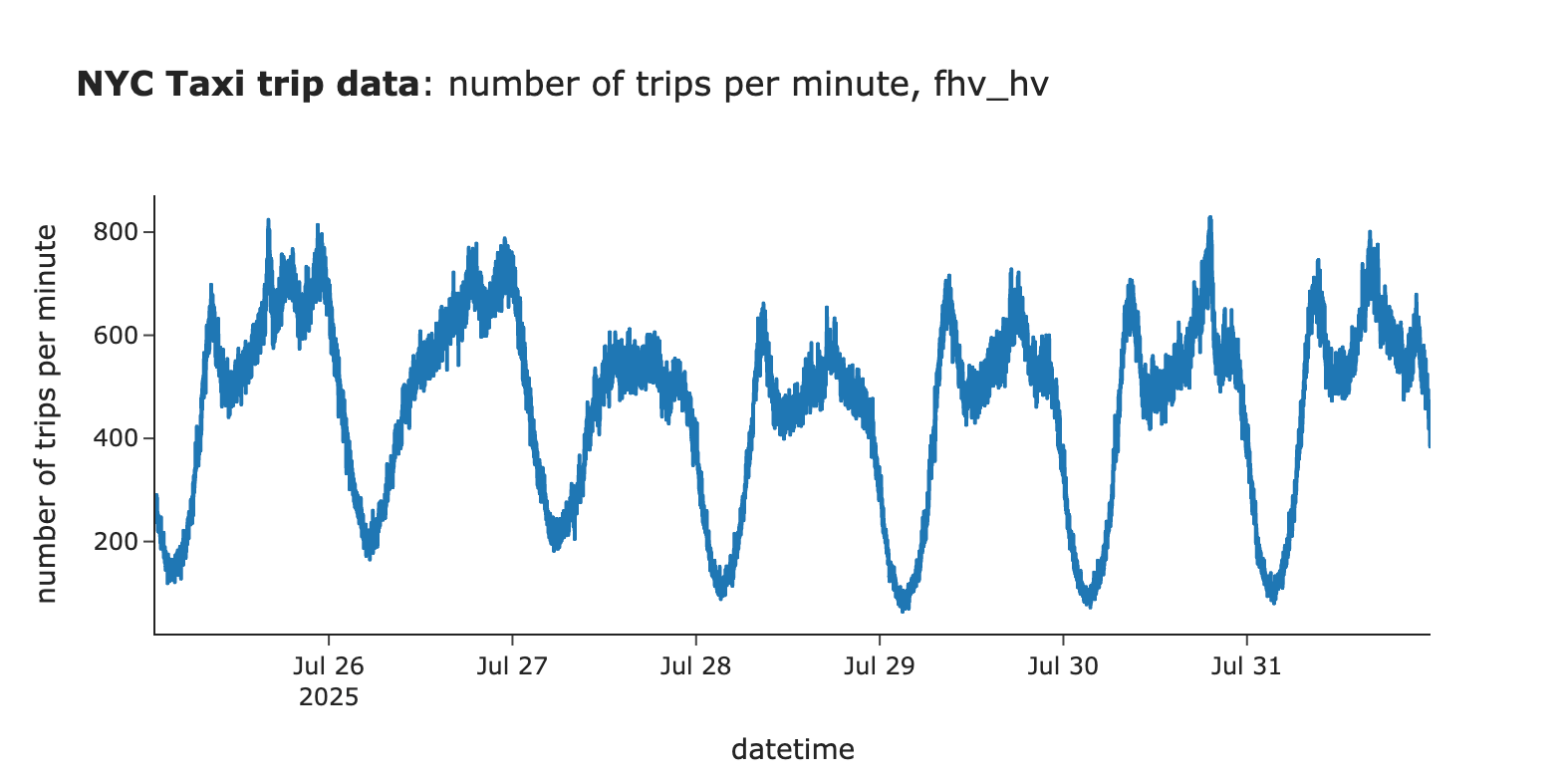
图片作者提供
构建第一个版本
现在,尝试我们的方法并基于真实数据构建置信区间。从一组默认的关键参数开始:
- 围绕当前时间戳的±15分钟时间窗口,
- 来自当前日期以及过去三周的同一工作日数据,
- 置信区间定义为±3个标准差。
接下来,创建几个包含业务逻辑的函数,用于计算置信区间并检查当前值是否超出其范围。
# returns the dataset of historic data
def get_distribution_for_ci(param, ts, n_weeks=3, n_mins=15):
tmp_df = df[['pickup_datetime', param]].rename(columns={param: 'value', 'pickup_datetime': 'dt'})
tmp = []
for n in range(n_weeks + 1):
lower_bound = (pd.to_datetime(ts) - pd.Timedelta(weeks=n, minutes=n_mins)).strftime('%Y-%m-%d %H:%M:%S')
upper_bound = (pd.to_datetime(ts) - pd.Timedelta(weeks=n, minutes=-n_mins)).strftime('%Y-%m-%d %H:%M:%S')
tmp.append(tmp_df[(tmp_df.dt >= lower_bound) & (tmp_df.dt <= upper_bound)])
base_df = pd.concat(tmp)
base_df = base_df[base_df.dt < ts]
return base_df
# calculates mean and std needed to calculate confidence intervals
def get_ci_statistics(param, ts, n_weeks=3, n_mins=15):
base_df = get_distribution_for_ci(param, ts, n_weeks, n_mins)
std = base_df.value.std()
mean = base_df.value.mean()
return mean, std
# iterating through all the timestamps in historic data
ci_tmp = []
for ts in tqdm.tqdm(df.pickup_datetime):
ci = get_ci_statistics('values', ts, n_weeks=3, n_mins=15)
ci_tmp.append(
{
'pickup_datetime': ts,
'mean': ci[0],
'std': ci[1],
}
)
ci_df = df[['pickup_datetime', 'values']].copy()
ci_df = ci_df.merge(pd.DataFrame(ci_tmp), how='left', on='pickup_datetime')
# defining CI
ci_df['ci_lower'] = ci_df['mean'] - 3 * ci_df['std']
ci_df['ci_upper'] = ci_df['mean'] + 3 * ci_df['std']
# defining whether value is outside of CI
ci_df['outside_of_ci'] = (ci_df['values'] < ci_df['ci_lower']) | (ci_df['values'] > ci_df['ci_upper'])
结果分析
接下来审视一下结果。首先,发现了相当多的假阳性触发(置信区间外的一次性点,似乎是由于正常的变异性)。
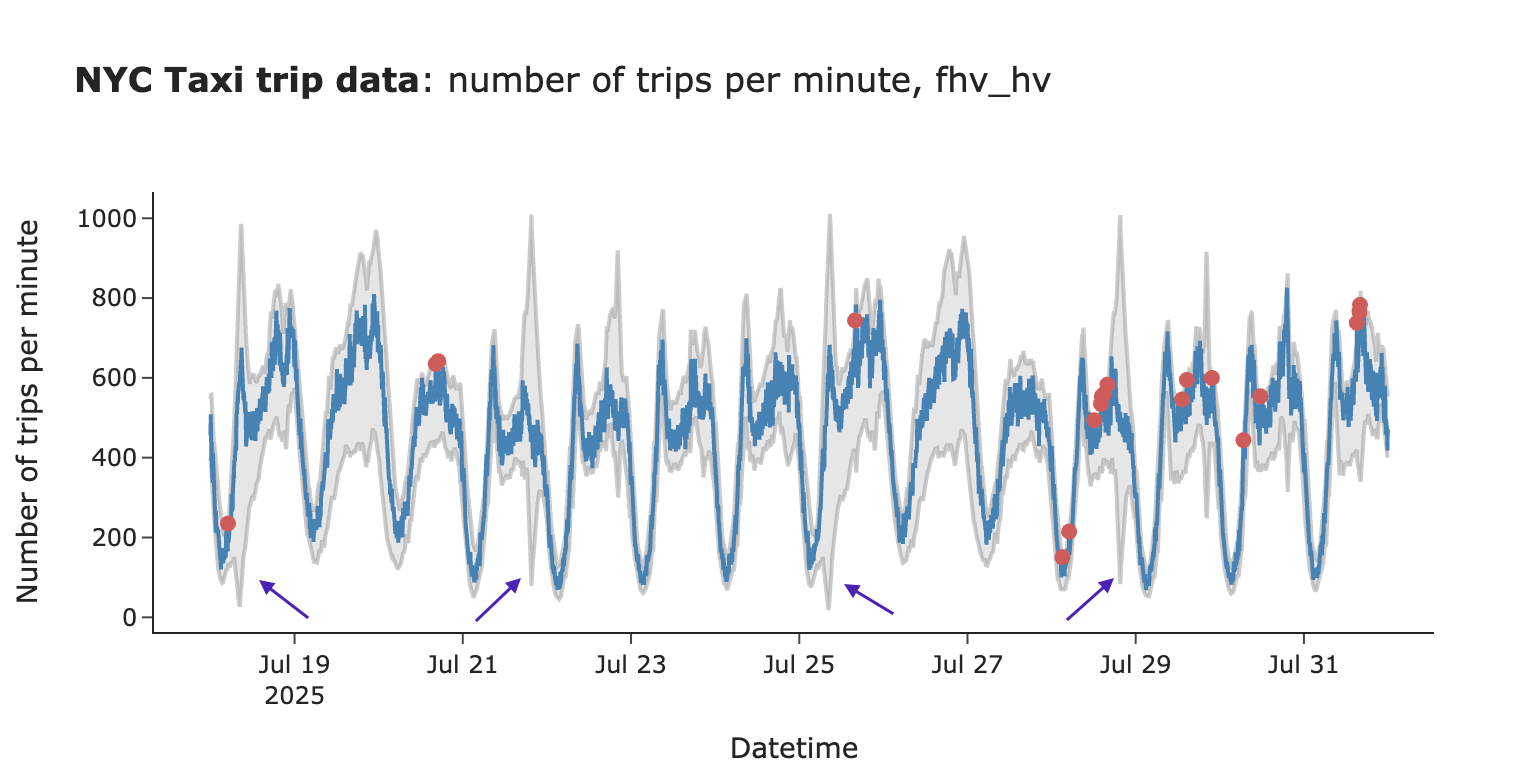
图片作者提供
有两种方法可以调整算法来解决这个问题:
- 置信区间不必是对称的。对乘车次数的增加可能不那么关注,因此可以对上限使用更高的系数(例如,使用5而不是3)。
- 数据波动性较大,偶尔会有单个点超出置信区间的异常情况。为了减少此类假阳性告警,可以使用更稳健的逻辑,仅在多个点超出置信区间时才触发告警(例如,最近5个点中至少有4个,或最近10个点中至少有8个)。
然而,当前的置信区间还存在另一个潜在问题。正如所见,在许多情况下,置信区间过宽。这看起来不正常,可能会降低监控的灵敏度。
通过一个例子来理解为何会发生这种情况。用于估计置信区间的分布是双峰的,这导致标准差更高,置信区间更宽。这是因为7月14日晚上的乘车次数显著高于其他几周。
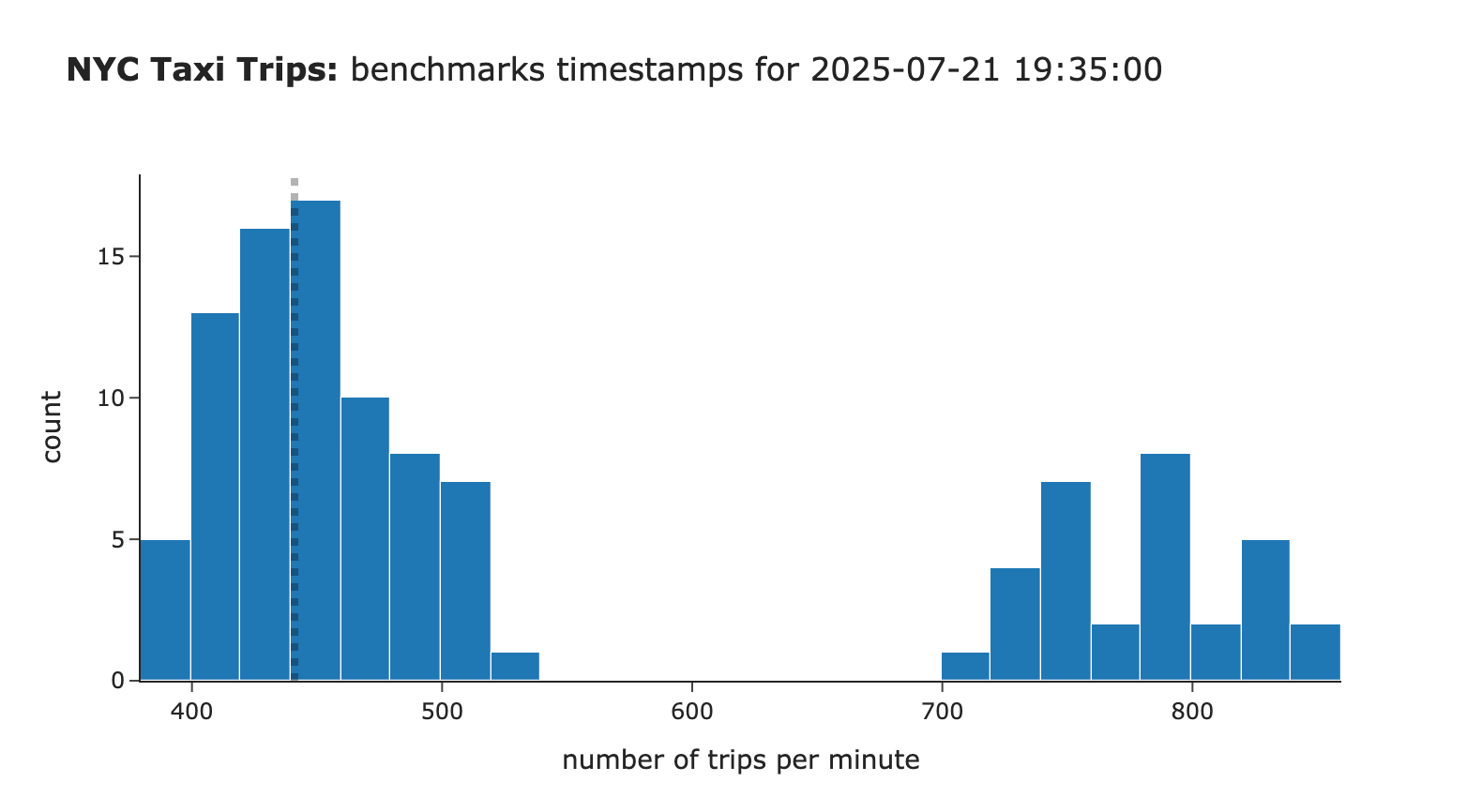
图片作者提供
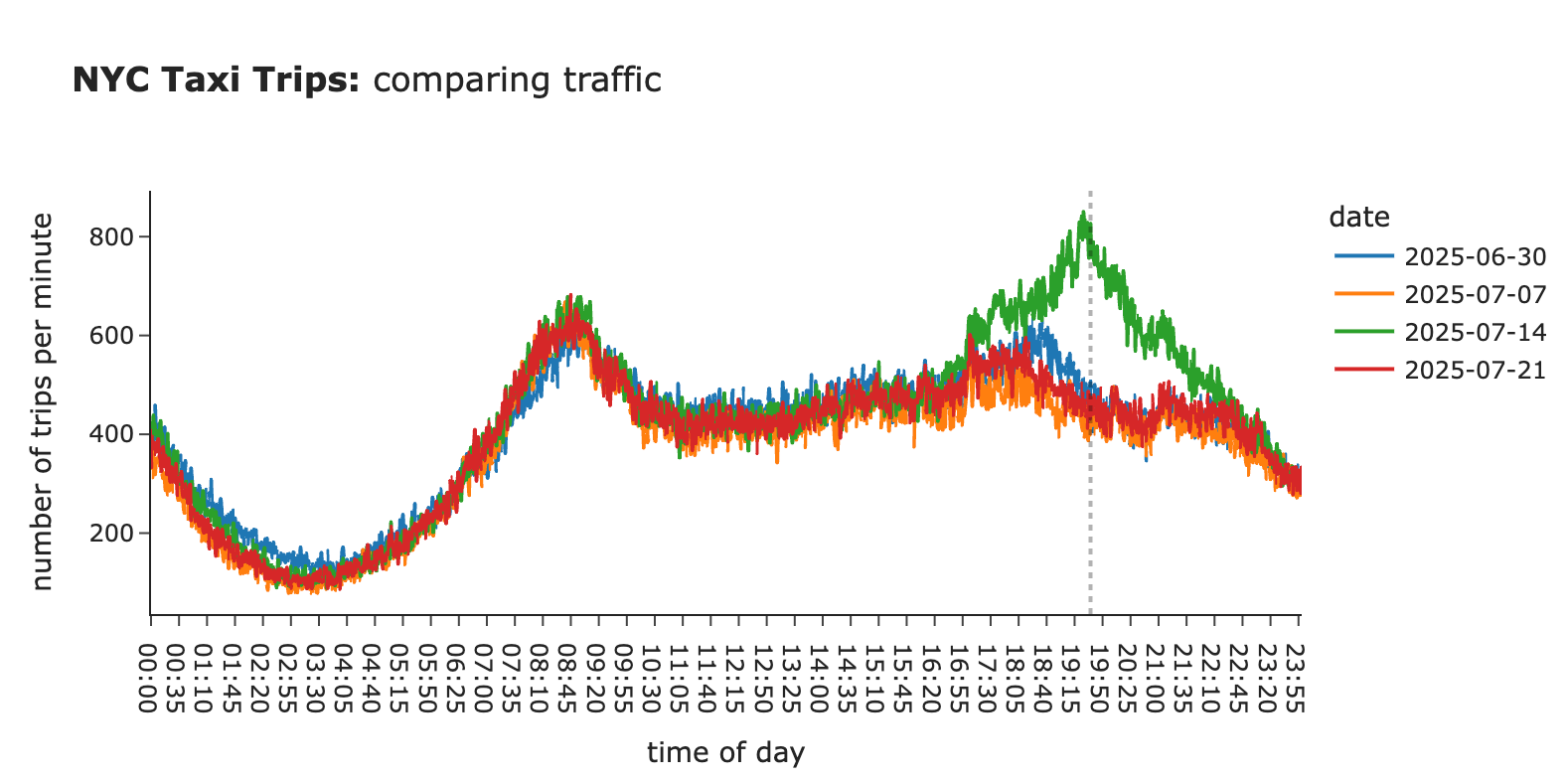
图片作者提供
因此,遇到了过去影响置信区间的异常。有两种方法可以解决这个问题:
- 如果进行持续监控,并且知道7月14日出现了异常高需求,那么在构建置信区间时可以排除这些时期。这种方法需要一些纪律来跟踪这些异常,但会带来更准确的结果。
- 当然,也总有一种“快速粗暴”的方法:在构建置信区间时,可以直接删除或截断异常值。
提高准确性
经过第一次迭代后,我们确定了监控方法的几个潜在改进点:
- 对上限使用更高的系数,因为对增加的关注度较低。使用了6个标准差而不是3个。
- 处理异常值,以过滤掉过去的异常。尝试了移除或截断前10-20%的异常值,发现在将周期增加到5周的同时截断20%的效果最好。
- 仅当最近5个点中有4个超出置信区间时才发出告警,以减少由正常波动引起的假阳性告警数量。
接下来看看代码实现。已更新get_ci_statistics中的逻辑,以适应处理异常值的不同策略。
def get_ci_statistics(param, ts, n_weeks=3, n_mins=15, show_vis = False, filter_outliers_strategy = 'none',
filter_outliers_perc = None):
assert filter_outliers_strategy in ['none', 'clip', 'remove'], "filter_outliers_strategy must be one of 'none', 'clip', 'remove'"
base_df = get_distribution_for_ci(param, ts, n_weeks, n_mins, show_vis)
if filter_outliers_strategy != 'none':
p_upper = base_df.value.quantile(1 - filter_outliers_perc)
p_lower = base_df.value.quantile(filter_outliers_perc)
if filter_outliers_strategy == 'clip':
base_df['value'] = base_df['value'].clip(lower=p_lower, upper=p_upper)
if filter_outliers_strategy == 'remove':
base_df = base_df[(base_df.value >= p_lower) & (base_df.value <= p_upper)]
std = base_df.value.std()
mean = base_df.value.mean()
return mean, std
还需要更新定义outside_of_ci参数的方式。
for ts in tqdm.tqdm(ci_df.pickup_datetime):
tmp_df = ci_df[(ci_df.pickup_datetime <= ts)].tail(5).copy()
tmp_df = tmp_df[~tmp_df.ci_lower.isna() & ~tmp_df.ci_upper.isna()]
if tmp_df.shape[0] < 5:
continue
tmp_df['outside_of_ci'] = (tmp_df['values'] < tmp_df['ci_lower']) | (tmp_df['values'] > tmp_df['ci_upper'])
if tmp_df.outside_of_ci.map(int).sum() >= 4:
anomalies.append(ts)
ci_df['outside_of_ci'] = ci_df.pickup_datetime.isin(anomalies)
可以看到,置信区间现在显著变窄(不再有异常宽的置信区间),并且由于增加了上限系数,告警数量也大大减少。
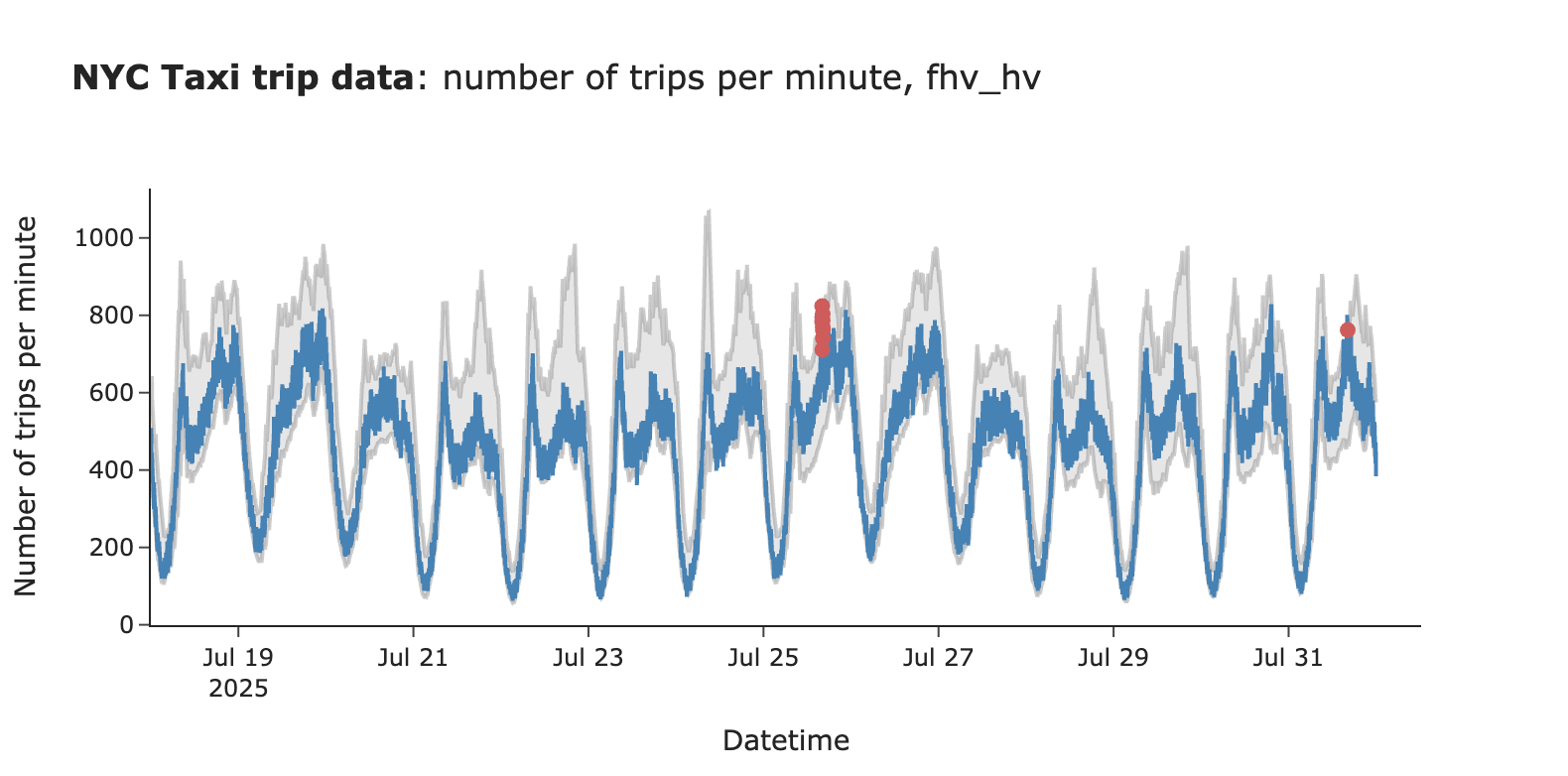
图片作者提供
接下来调查发现的两个告警。最近两周的这两个告警,与前几周的流量相比,看起来是合理的。
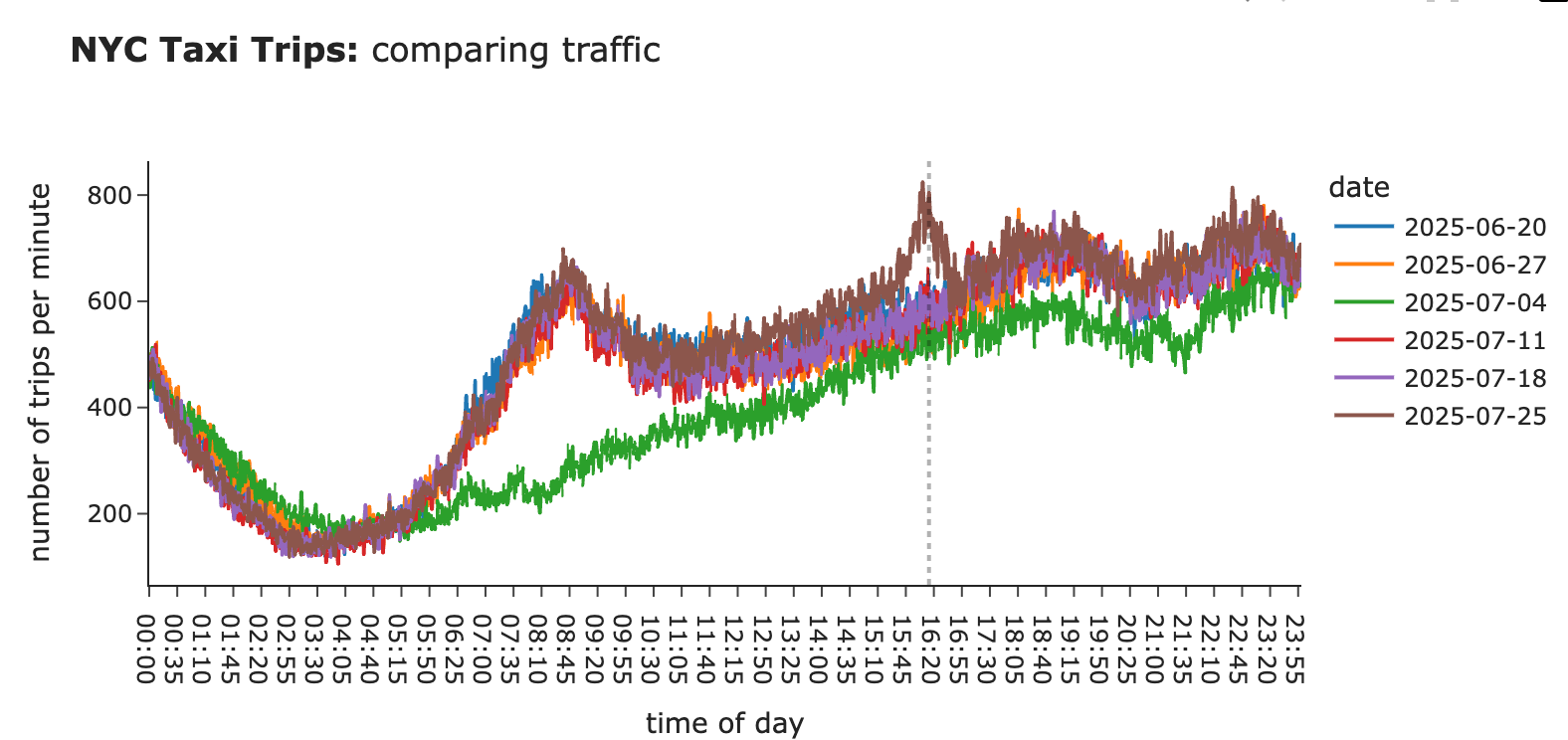
图片作者提供
实用小贴士:这张图也提醒我们,理想情况下应该考虑公共假期,并在计算置信区间时将其排除在外或作为周末处理。
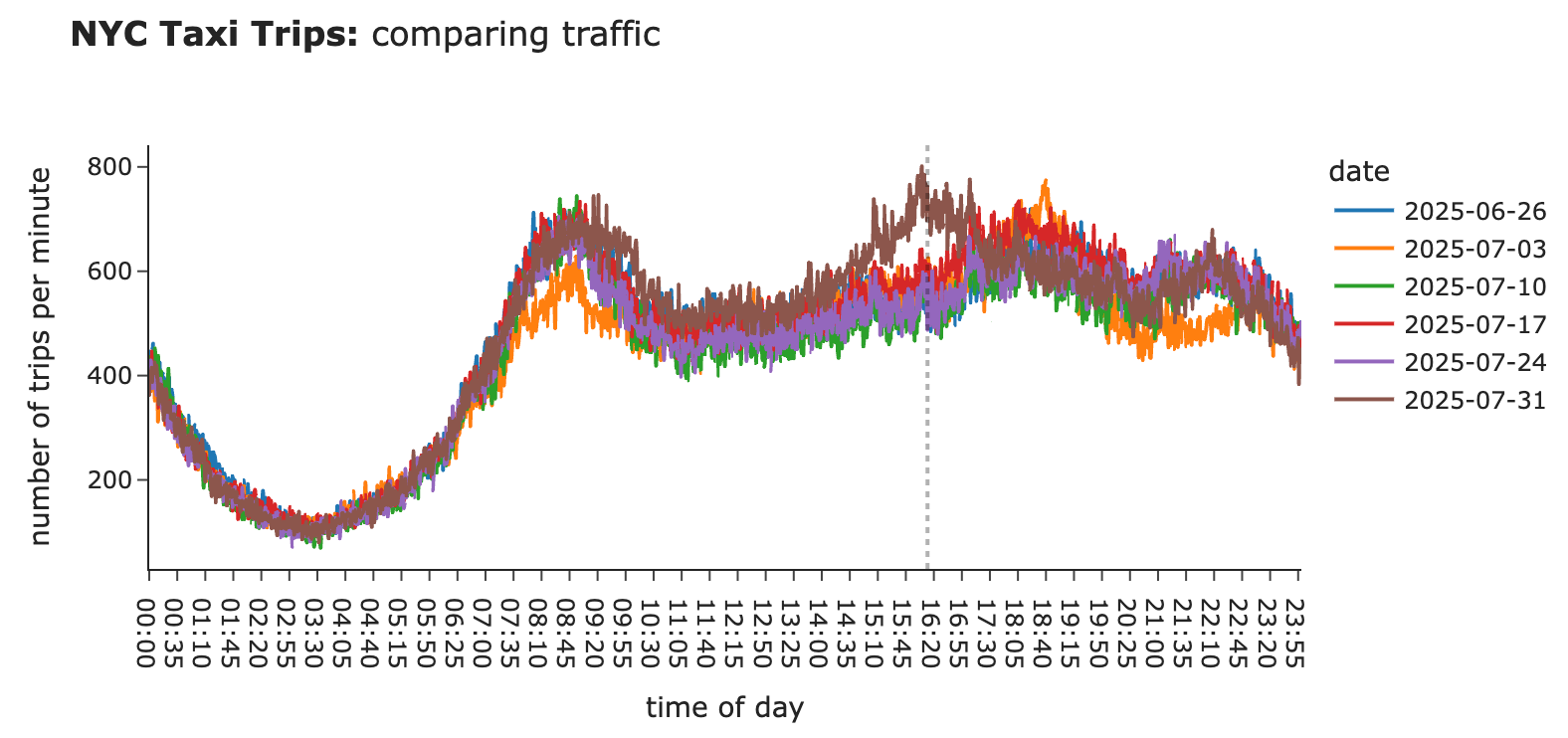
图片作者提供
因此,新的监控方法完全合理。然而,也存在一个缺点:通过仅寻找最近5分钟中有4分钟超出置信区间的情况,可能会延迟在一切都完全崩溃的情况下的告警。为了解决这个问题,实际上可以使用两个置信区间:
- “末日”置信区间:一个宽泛的置信区间,即使单个点超出范围也意味着需要立即采取行动。
- “事件”置信区间:之前构建的那个,在指标下降不那么关键时,可能会等待5-10分钟才触发告警。
为我们的案例定义两个置信区间。
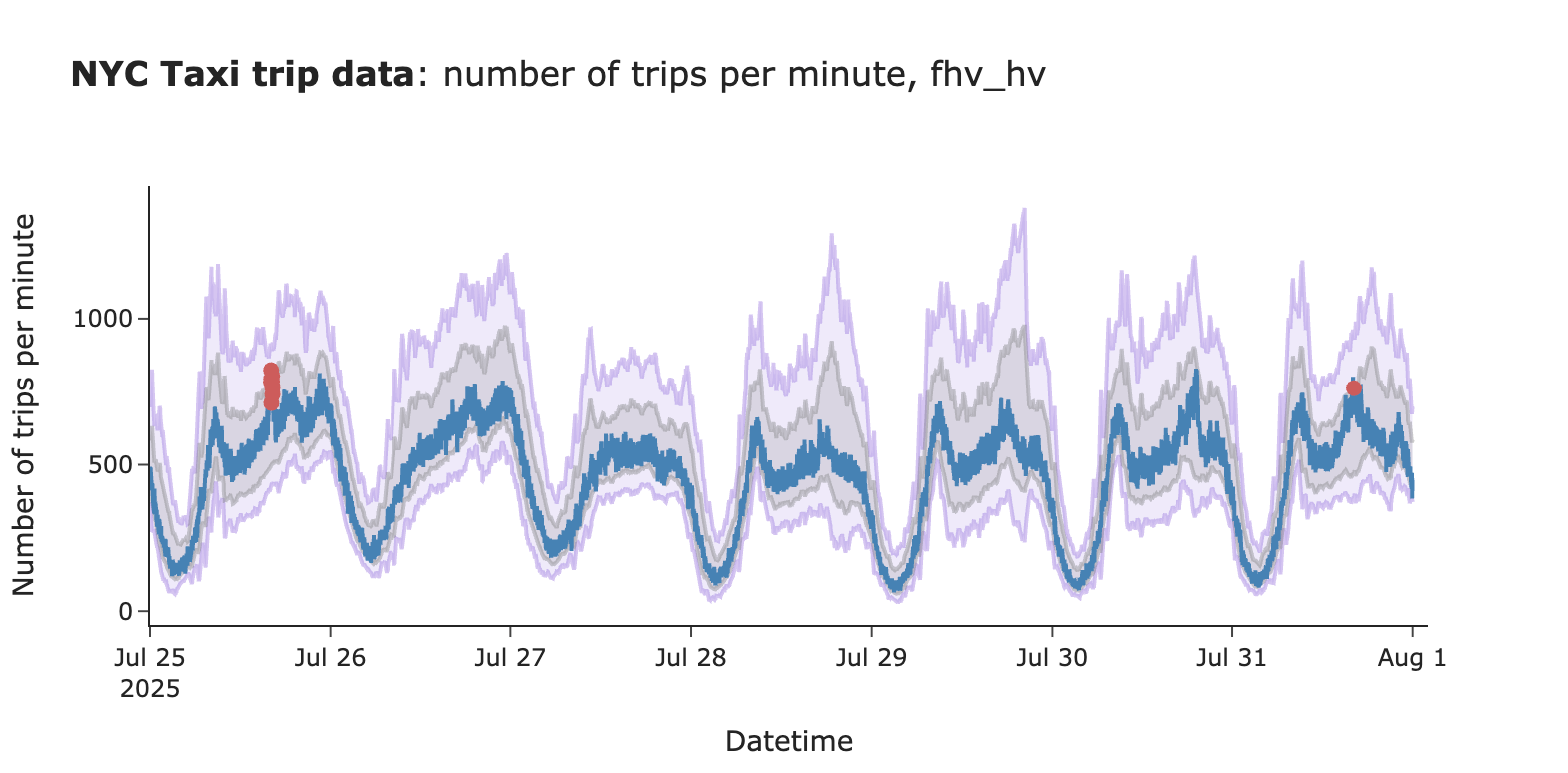
图片作者提供
这是一种平衡的方法,兼顾了两者之长:可以在出现严重问题时迅速反应,同时仍能控制假阳性。至此,我们取得了良好的结果,并准备继续前进。
在异常情况下测试监控系统
已经确认我们的方法在常规业务场景下表现良好。然而,进行一些压力测试也很有价值,即模拟想要捕获的异常情况,并检查监控系统的表现。在实践中,针对先前已知的异常进行测试,以了解它如何处理真实世界的例子,是值得的。
在我们的案例中,没有过去的异常变更日志,因此模拟了乘车次数下降20%的情况,而我们的方法立即捕获了它。
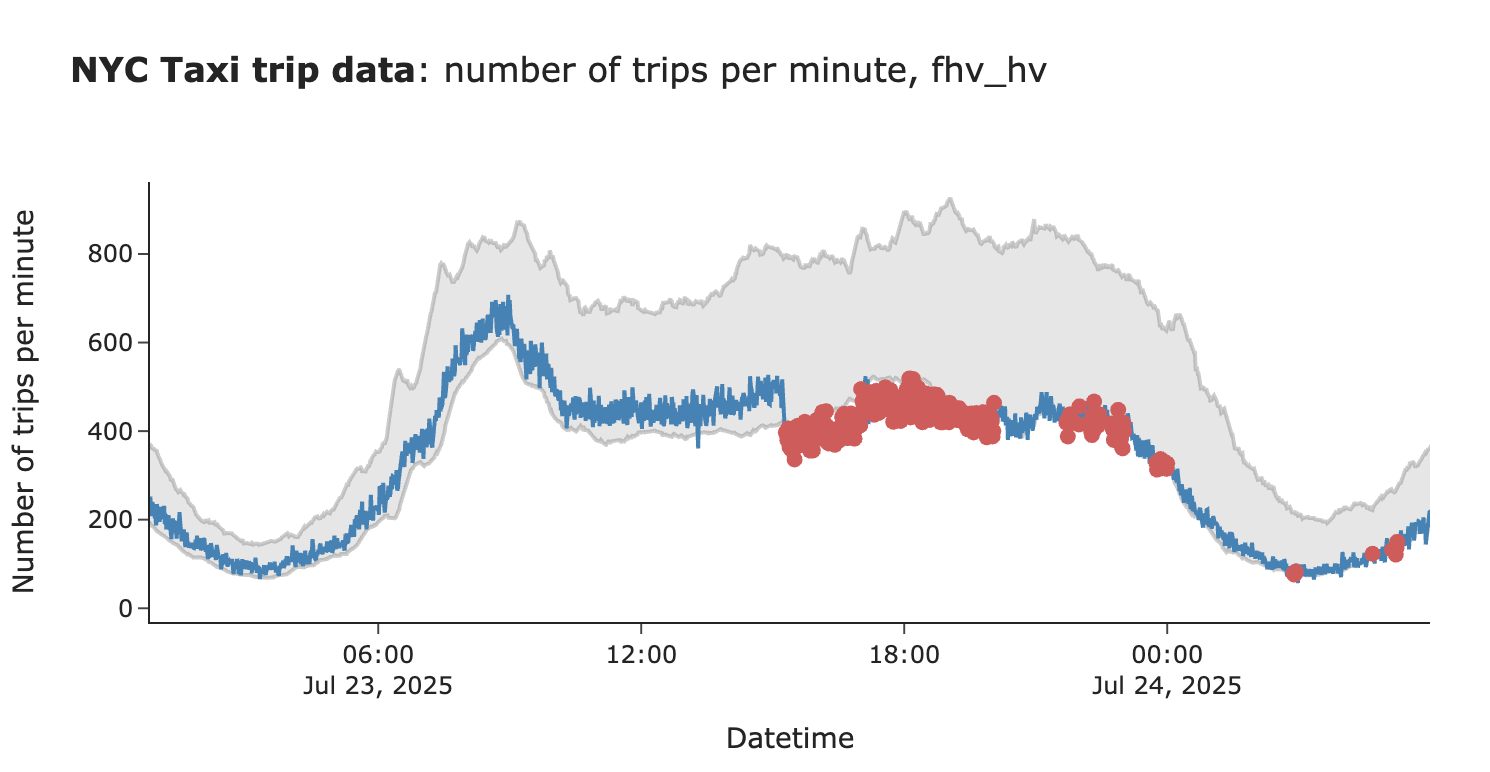
图片作者提供
这种阶跃变化在现实生活中可能很棘手。想象一下,如果失去了一个合作伙伴,并且这个较低的水平成为指标的新常态。在这种情况下,调整监控系统也很有价值。如果能够根据当前状态重新计算历史指标(例如,通过过滤掉失去的合作伙伴的数据),那将是理想的,因为这将使监控恢复正常。如果这不可行,可以调整历史数据(例如,减去20%的流量作为我们对变化的估计),或者删除变化之前的所有数据,仅使用新数据来构建置信区间。

图片作者提供
再看一个棘手的真实世界案例:缓慢衰减。如果指标日复一日缓慢下降,我们的实时监控可能无法捕获它,因为置信区间会随之移动。为了捕获这种情况,值得进行粒度较低的监控(例如每日、每周甚至每月)。
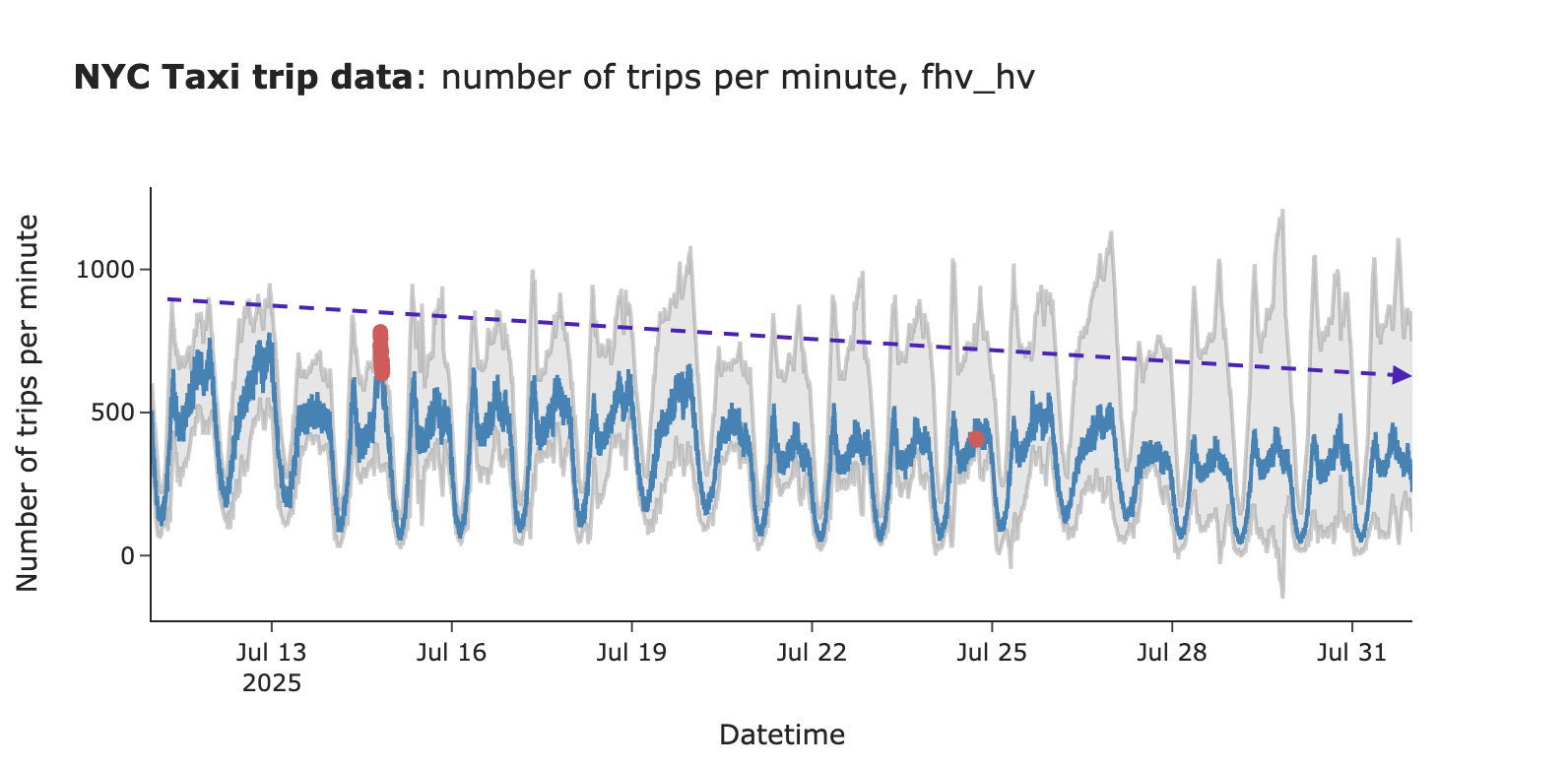
图片作者提供
完整代码可在GitHub上找到。
运维挑战
我们已经讨论了告警和监控系统背后的数学原理。然而,一旦开始将系统部署到生产环境中,可能会遇到其他一些细微的挑战。因此,在总结之前,希望涵盖这些内容。
数据延迟。在我们的示例中没有遇到这个问题,因为处理的是历史数据,但在现实生活中,需要处理数据延迟。数据通常需要一些时间才能到达数据仓库。因此,需要学会区分数据尚未到达的情况与实际影响客户体验的事件。最直接的方法是查看历史数据,确定典型的延迟,并过滤掉最后5-10个数据点。
不同细分的不同灵敏度。可能不仅希望监控主要KPI(例如乘车次数),还希望按多个细分(例如合作伙伴、区域等)进行分解监控。增加更多细分总是有益的,因为它有助于发现特定细分中的微小变化(例如,曼哈顿地区存在问题)。然而,正如前面提到的,也存在缺点:更多细分意味着需要处理更多的假阳性告警。为了控制这种情况,可以对不同细分使用不同的灵敏度级别(例如,对主要KPI使用3个标准差,对细分使用5个标准差)。
更智能的告警系统。此外,在监控许多细分时,让告警系统更智能一些是值得的。假设对主要KPI和99个细分进行了监控。现在,想象一下发生了全球性中断,所有地方的乘车次数都下降了。在接下来的5分钟内,将(希望)收到100条关于问题发生的通知。这不是一个理想的体验。为了避免这种情况,可以构建逻辑来过滤掉冗余通知。例如:
- 如果在过去3小时内收到了相同的通知,则不再触发新的告警。
- 如果收到关于主要KPI下降以及超过3个细分下降的通知,则只告警主要KPI的变化。
总而言之,告警疲劳是真实存在的,因此尽量减少噪音是值得的。
就是这样!我们已经涵盖了告警和监控的整个主题,希望现在您已经完全有能力设置自己的系统。
总结
我们已经涵盖了告警和监控的许多方面。接下来,通过一个分步指南来总结如何开始监控KPIs。
- 第一步是收集过去的异常变更日志。这既可以作为系统的一组测试用例,也可以在计算置信区间时过滤掉异常时期。
- 接下来,构建一个原型并在历史数据上运行。可以从最高级别的KPI开始,尝试几种可能的配置,并观察它捕捉先前异常的效果,以及是否生成大量虚假告警。此时,应该会有一个可行的解决方案。
- 然后将其投入生产环境进行试用,因为这将是处理数据延迟并观察监控实际性能的地方。运行2-4周,并调整参数以确保其按预期工作。
- 之后,与同事分享监控系统并开始扩大范围,纳入其他细分。不要忘记持续将所有异常添加到变更日志中,并建立反馈循环以不断改进系统。
就是这样!现在可以安心了,因为自动化系统正在密切关注您的KPIs(但仍然需要时不时地检查它们,以防万一)。