在构建回归模型时,其核心在于通过数据拟合一条直线,从而预测未来的数值。在此过程中,通常会首先对数据进行可视化,以便直观了解数据的分布形态、潜在模式以及变量间的关系。
数据初步观察可能呈现出正向线性关系,但为了确证这一趋势,需要通过计算皮尔逊相关系数来进行量化验证。该系数能够准确衡量数据点与理想线性关系的接近程度。
为了更好地理解皮尔逊相关系数,可以参考一个简单的薪资数据集。
该数据集包含以下两个核心列:
YearsExperience (工作经验年限): 个人工作的时间长度(以年为单位)
Salary (薪资) (目标变量): 对应的年度薪资,单位为美元。
在此基础上,目标是构建一个能够根据工作经验年限预测薪资的模型。
考虑到只有一个预测变量(工作经验年限)和一个连续的目标变量(薪资),可以推断出使用简单线性回归模型是解决此类问题的有效方法。
然而,是否可以直接套用简单线性回归算法呢?
答案是否定的。
线性回归模型的应用存在多项前提假设,其中最关键的一项便是线性关系。
因此,在应用模型之前,必须对数据是否满足线性假设进行检验,而检验的常用方法就是计算相关系数。
那么,究竟何为线性关系?
通过一个具体的例子,将有助于更好地理解这一概念。
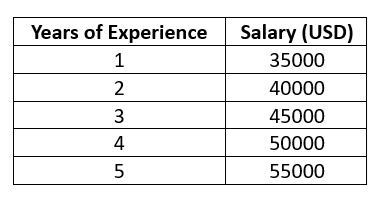
从上表中可以清晰地观察到,工作经验每增加一年,薪资便稳定增长5,000美元。
这种恒定的变化率,使得当这些数值被绘制成图时,会形成一条完美的直线。
这种关系即被定义为线性关系。
在简单线性回归中,核心在于通过数据拟合一条回归线来预测未来值。这种预测方法的有效性,严格依赖于数据本身是否呈现出显著的线性关系。
因此,在应用模型前,对数据进行线性关系检验至关重要。
为此,接下来将计算数据间的相关系数。
在此之前,通常会先利用散点图对数据进行可视化,以便初步了解两个变量之间的潜在关系。
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
# 导入数据集
df = pd.read_csv("C:/Salary_dataset.csv")
# 设置绘图风格
sns.set(style="whitegrid")
# 创建散点图
plt.figure(figsize=(8, 5))
sns.scatterplot(x='YearsExperience', y='Salary', data=df, color='blue', s=60)
plt.title("散点图:工作经验年限 vs 薪资")
plt.xlabel("工作经验年限")
plt.ylabel("薪资 (美元)")
plt.tight_layout()
plt.show()
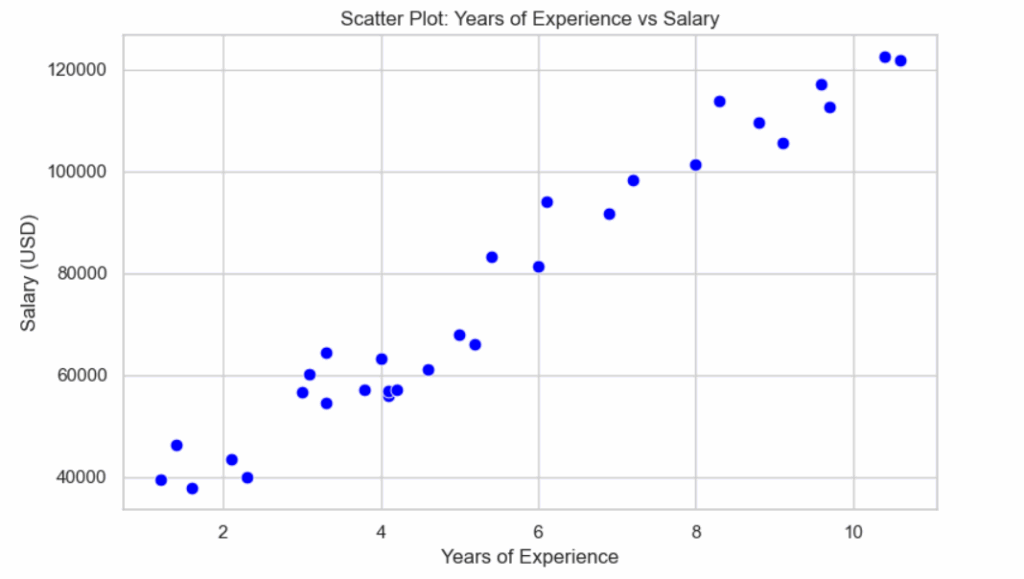
从散点图中可以清晰地观察到,随着工作经验年限的增加,薪资也呈现出明显的增长趋势。
尽管数据点并未构成一条完美的直线,但整体关系依然表现出强烈的线性特征。
为了进一步验证这一观察结果,接下来将计算皮尔逊相关系数。
import pandas as pd
# 导入数据集
df = pd.read_csv("C:/Salary_dataset.csv")
# 计算皮尔逊相关系数
pearson_corr = df['YearsExperience'].corr(df['Salary'], method='pearson')
print(f"皮尔逊相关系数: {pearson_corr:.4f}")
计算得到的皮尔逊相关系数为0.9782。
相关系数的取值范围始终介于-1到+1之间。
具体解读如下:
接近1:表示存在强烈的正向线性关系。
接近0:表示几乎不存在线性关系。
接近-1:表示存在强烈的负向线性关系。
在此次计算中,相关系数的值为0.9782,这表明数据点高度符合直线模式,且变量之间存在非常强的正向线性关系。
由此可以得出结论,简单线性回归模型非常适合用于描述和预测这种关系。
那么,这个皮尔逊相关系数究竟是如何计算得出的呢?
为了清晰展示计算过程,接下来将从原始数据集中抽取一个包含10个数据点的样本进行分析。
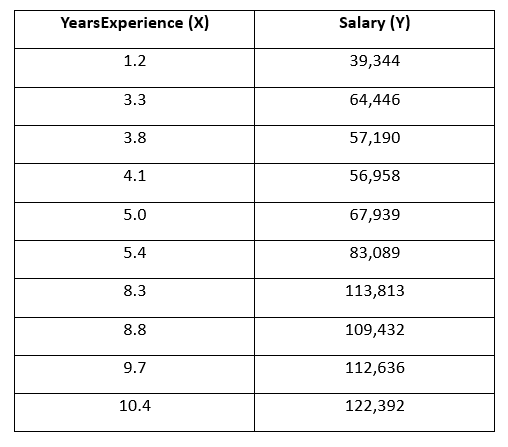
现在,开始逐步计算皮尔逊相关系数。
当变量X和Y同时增加时,这种相关性被称为正相关。相反,如果一个变量增加而另一个变量减少,则这种相关性被称为负相关。
首先,需要计算每个变量的方差。
方差是衡量数据点离其平均值分散程度的指标。
首先从计算变量X(工作经验年限)的方差开始。
为此,首先需要计算X的平均值。
X¯=1 n∑i=1 n X i
=1.2+3.3+3.8+4.1+5.0+5.4+8.3+8.8+9.7+10.4 10
=70.0 10
=7.0
接下来,将每个数据点减去其平均值,然后对结果进行平方,以消除负值的影响。
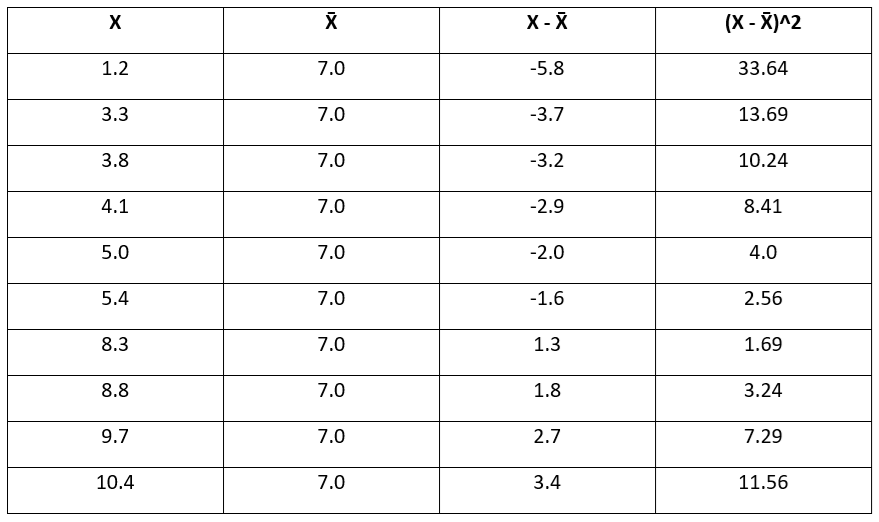
至此,已计算出每个数据点与平均值之间的平方偏差。
现在,通过计算这些平方偏差的平均值,可以得到变量X的方差。
样本方差 X=1 n–1∑i=1 n(X i–X¯)2
=33.64+13.69+10.24+8.41+4.00+2.56+1.69+3.24+7.29+11.56 10–1
=96.32 9≈10.70
此处除以‘n-1’是因为处理的是样本数据,使用‘n-1’能够提供对方差的无偏估计。
变量X的样本方差为10.70,这意味着工作经验年限的数据点平均偏离其均值10.70平方单位。
由于方差是一个平方值,为了使其单位与原始数据一致,需要对其进行平方根运算。
这一结果即为标准差。
s X=样本方差−−−−−−−−−−−−−√=10.70−−−−√≈3.27
变量X的标准差为3.27,这表示工作经验年限的数据点大约分布在均值上下3.27年的范围内。
以同样的方法,计算变量‘Y’(薪资)的方差和标准差。
Y¯=1 n∑i=1 n Y i
=39344+64446+57190+56958+67939+83089+113813+109432+112636+122392 10
=827239 10
=82,723.90
样本方差 Y=1 n–1∑(Y i–Y¯)2
=7,898,632,198.90 9=877,625,799.88
标准差 Y 为 s Y=877,625,799.88−−−−−−−−−−−−√≈29,624.75
至此,已完成变量‘X’和‘Y’的方差和标准差计算。
接下来,关键的一步是计算X和Y之间的协方差。
目前已拥有X和Y的平均值,以及各数据点与其各自平均值的偏差。
现在,将这些偏差相乘,以观察这两个变量如何共同变动。
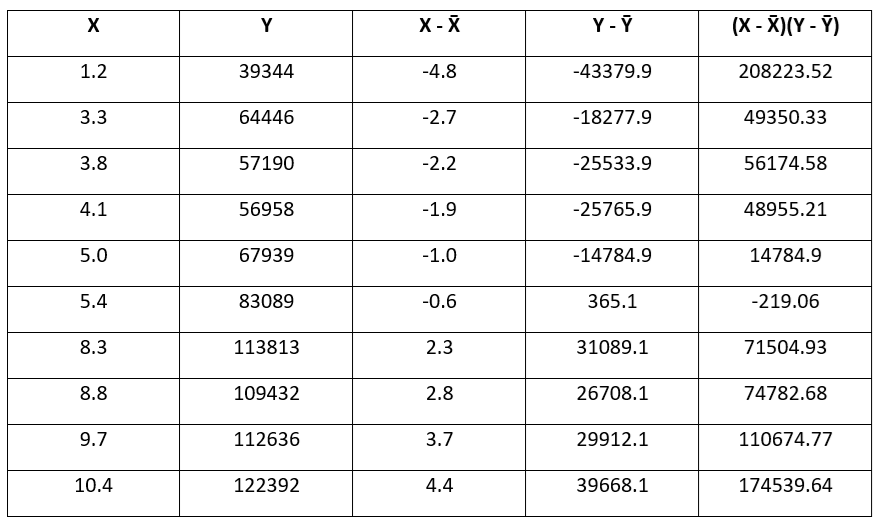
通过将这些偏差相乘,旨在捕捉X和Y之间同步变动的模式。
如果X和Y都高于各自的平均值,那么它们的偏差均为正值,乘积也为正。
如果X和Y都低于各自的平均值,那么它们的偏差均为负值,而负负得正,乘积同样为正。
如果一个变量高于平均值而另一个低于平均值,则乘积为负。
这个乘积能够揭示这两个变量是倾向于朝相同方向变动(同增或同减),还是朝相反方向变动。
利用偏差乘积的总和,现在可以计算出样本协方差。
样本协方差=1 n–1∑i=1 n(X i–X¯)(Y i–Y¯)
=808771.5 10–1
=808771.5 9=89,863.5
计算得到的样本协方差为89863.5。这个正值表明,随着工作经验的增加,薪资也倾向于增加。
然而,协方差的数值大小受到变量单位(年 × 美元)的影响,因此其自身不具备直接的可解释性。
这个值主要用于指示变量变动的方向。
接下来,将协方差除以X和Y标准差的乘积。
这一操作将得到皮尔逊相关系数,它本质上是协方差的一种标准化形式。
由于X的标准差单位为“年”,Y的标准差单位为“美元”,二者相乘后的单位是“年 × 美元”。
当协方差被它们的乘积除以时,单位会自动抵消,从而使皮尔逊相关系数成为一个无量纲的数值。
但除以标准差的主要目的在于对协方差进行标准化,使得结果更易于理解,并能够在不同数据集之间进行有效的比较。
r=Cov(X,Y)s X⋅s Y=89,863.5 3.27×29,624.75=89,863.5 96,992.13≈0.9265
因此,计算得到的皮尔逊相关系数(r)为0.9265。
这个数值表明,工作经验年限与薪资之间存在非常强的正向线性关系。
通过以上步骤,即可计算出皮尔逊相关系数。
皮尔逊相关系数的完整公式如下:
r=Cov(X,Y)s X⋅s Y=1 n–1∑n i=1(X i–X¯)(Y i–Y¯)1 n–1∑n i=1(X i–X¯)2−−−−−−−−−−−−−−√⋅1 n–1∑n i=1(Y i–Y¯)2−−−−−−−−−−−−−−√
=∑n i=1(X i–X¯)(Y i–Y¯)∑n i=1(X i–X¯)2−−−−−−−−−−−√⋅∑n i=1(Y i–Y¯)2−−−−−−−−−−−√
在计算皮尔逊相关系数之前,需要确保数据满足以下几个前提条件:
- 变量之间的关系应呈线性。
- 两个变量都必须是连续型和数值型数据。
- 数据中不应存在显著的异常值。
- 数据应大致符合正态分布。
数据集
本文所使用的数据集是薪资数据集。
该数据集在Kaggle上公开可用,并采用知识共享零(CC0公共领域)许可。这意味着它可以在没有任何限制的情况下,自由地用于非商业和商业目的的 使用、修改和分享。
本文旨在清晰阐述皮尔逊相关系数的计算方法及其应用场景,希望能帮助读者建立对该概念的深刻理解。