在前一篇文章中,探讨了基于距离的K-Means聚类方法。
进一步地,为了改进距离的度量方式,可以引入方差,从而得到马氏距离。
因此,如果K-Means是最近质心分类器的无监督版本,那么一个自然而然的问题是:
二次判别分析(QDA)的无监督版本又是什么?
这意味着,如同QDA一样,每个簇现在不仅需要用其均值来描述,还需要用其方差来描述(如果特征数量超过2个,还需要加入协方差)。但这里的一切都是在没有标签的情况下学习的。
所以,其中的思路就很清晰了,对吗?
没错,这个模型的名字就是高斯混合模型(GMM)……
GMM与模型命名背后的故事
正如常见的情况,模型名称往往源于历史原因。如果这些模型并非一同被发现,其命名并不总是为了凸显模型之间的联系。
不同的研究者、不同的时期、不同的应用场景……最终导致了一些名称有时会掩盖思想背后的真实结构。
在这里,“高斯混合模型”这个名字仅仅意味着数据被表示为多个高斯分布的混合。
如果遵循与K-Means相同的命名逻辑,将其称为类似K-高斯混合的名称或许会更清晰。
因为在实践中,除了使用均值,还加入了方差。并且可以直接使用马氏距离,或者其他利用均值和方差的加权距离。但高斯分布提供了更容易解释的概率。
因此,需要选择一个高斯分量的数量k。
顺便提一下,GMM并非唯一具有这种特性的模型。
事实上,整个机器学习框架实际上比它所包含的许多模型要新得多。这些技术大多最初是在统计学、信号处理、计量经济学或模式识别领域发展起来的。
后来,在很久以后,如今被称为“机器学习”的领域才出现,并将所有这些模型归拢到一个框架下。但名称并未改变。
所以,今天使用的词汇混合了来自不同时代、不同社区和不同意图的术语。
这就是为什么仅从名称来看,模型之间的关系并不总是显而易见的。
如果要用现代、统一的机器学习风格重新命名一切,整个图景实际上会清晰得多:
- GMM 将变成 K-高斯聚类
- QDA 将变成 最近高斯分类器
- LDA,则是各类别间方差相同的最近高斯分类器。
突然间,所有的联系都显现出来了:
- K-Means ↔ 最近质心分类器
- GMM ↔ 最近高斯分类器(QDA)
这就是为什么GMM在K-Means之后显得如此自然。如果K-Means通过最近的质心对点进行分组,那么GMM则通过最近的高斯形状对它们进行分组。
为什么要用整个章节来讨论名称?
实际上,既然已经涵盖了K-Means算法,并且已经完成了从最近质心分类器到QDA的过渡,那么对这个算法已经了如指掌,其训练算法也不会改变……
那么这个训练算法的名字是什么?
哦,是劳埃德算法。
事实上,在K-Means被如此命名之前,它只是被称为劳埃德算法,由斯图尔特·劳埃德于1957年发表。后来,机器学习社区才将其改为“K-Means”。
而这个算法只操作均值,所以需要一个新名字,对吧?
想必已经猜到:期望最大化算法!
EM算法本质上是劳埃德思想的通用形式。劳埃德算法更新均值,而EM算法更新一切:均值、方差、权重和概率。
所以,关于GMM的一切都已经了解了!
但既然文章标题是“在Excel中实现GMM”,就不能在这里结束……
一维数据中的GMM
从一个简单的数据集开始,与K-Means中使用的相同:1, 2, 3, 11, 12, 13
嗯,两个高斯分布将具有相同的方差。可以考虑在Excel中尝试其他数字!
自然地,希望得到2个簇。
以下是不同的步骤。
初始化
从对均值、方差和权重的初始猜测开始。

GMM在Excel中的初始化步骤 – 作者供图
期望步骤(E步)
对于每个数据点,计算其属于每个高斯分布的可能性。

GMM在Excel中的期望步骤 – 作者供图
最大化步骤(M步)
利用这些概率,更新均值、方差和权重。

GMM在Excel中的最大化步骤 – 作者供图
迭代
重复E步和M步,直到参数稳定。
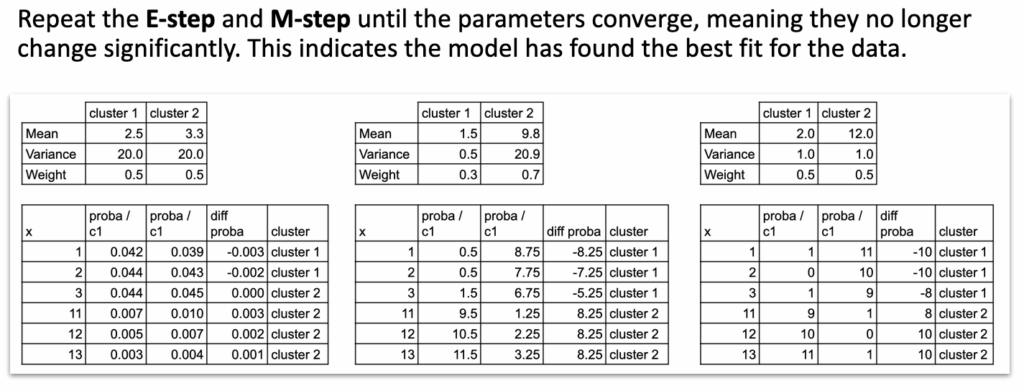
GMM在Excel中的迭代过程 – 作者供图
一旦公式可见,每一步都极其简单。
可以看到,EM算法无非就是更新平均值、方差和概率。
还可以进行一些可视化,以观察高斯曲线在迭代过程中的移动。
开始时,两条高斯曲线严重重叠,因为初始的均值和方差只是猜测。
曲线慢慢分离,调整其宽度,最终精确地落在两组数据点上。
通过绘制每次迭代的高斯曲线,可以直观地观察模型的学习过程:
- 均值滑向数据的中心
- 方差收缩以匹配每组数据的分布
- 重叠消失
- 最终形状与数据集的结构相匹配
这种视觉演变对建立直觉非常有帮助。一旦看到曲线移动,EM算法就不再是一个抽象算法,而变成了一个可以逐步跟踪的动态过程。
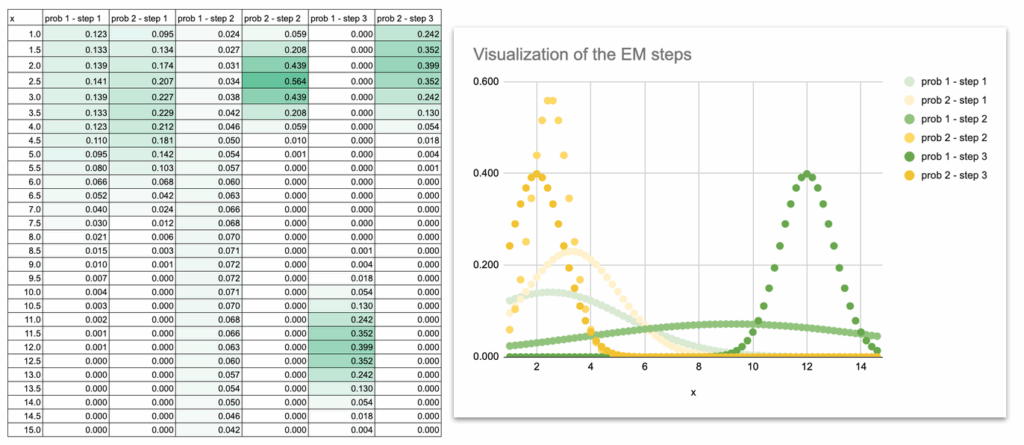
GMM在Excel中的可视化 – 作者供图
二维数据中的GMM
其逻辑与一维情况完全相同。概念上没有任何新内容。只是扩展了公式……
现在每个点有两个特征,而不是一个。
每个高斯分布现在必须学习:
- x1的均值
- x2的均值
- x1的方差
- x2的方差
- 以及两个特征之间的协方差项。
一旦在Excel中写出公式,就会发现过程完全保持不变:
实际上,如果查看截图,可能会想:“哇,公式好长啊!” 而且这还不是全部。
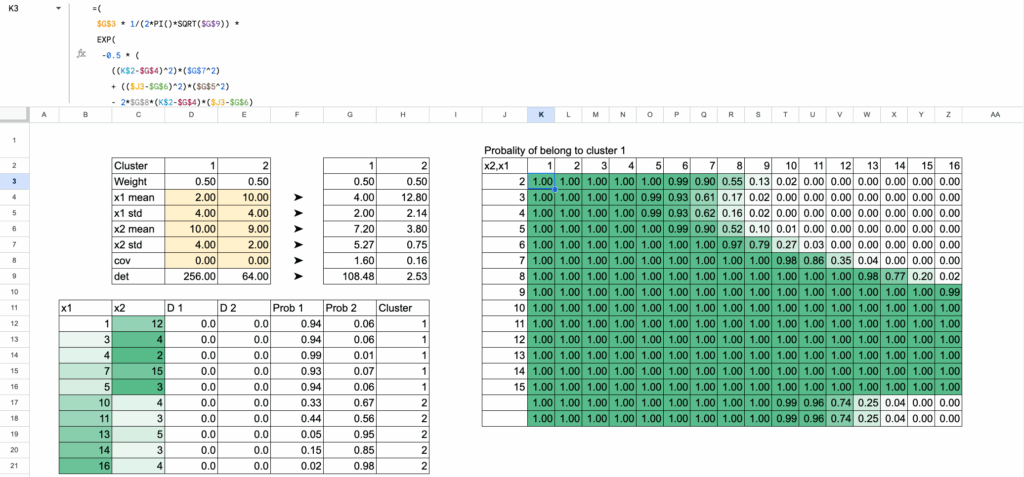
二维GMM在Excel中 – 作者供图
但不要被表象迷惑。公式长只是因为显式地写出了二维高斯密度:
- 一部分用于x1方向的距离
- 一部分用于x2方向的距离
- 协方差项
- 归一化常数
仅此而已。
这仅仅是密度公式在单元格中的逐项展开。
输入起来很长,但一旦看到结构就完全可以理解:一个加权距离,放在指数函数内,再除以行列式。
所以,是的,公式看起来很大……但其背后的思想极其简单。
结论
K-Means提供硬边界。
GMM提供概率。
一旦在Excel中写出EM公式,模型就变得易于跟踪:均值移动,方差调整,高斯分布自然地围绕数据稳定下来。