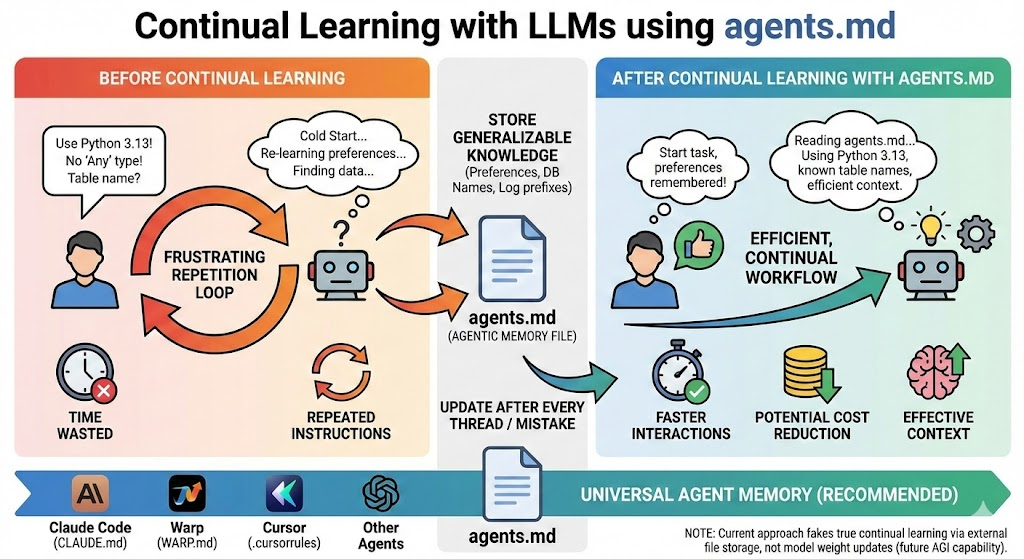
欢迎来到机器学习“降临日历”系列的第10天。感谢各位读者的持续关注。
这些Google Sheet文件经过多年的迭代与完善。每次发布前,都需要花费大量时间进行内容重组、布局清理与视觉优化,以确保其清晰易读。
今天,我们将聚焦于DBSCAN算法。
DBSCAN:一种非参数化模型
与局部离群因子算法类似,DBSCAN并非参数化模型。它不存储公式、规则或质心,也没有可供后续复用的紧凑型结构。
由于密度结构依赖于所有数据点,因此必须保留完整的数据集。
其全称为基于密度的带噪声空间聚类应用。
但需注意:这里的“密度”并非高斯密度。
它是一种基于计数的密度概念,核心在于衡量“有多少邻居离我足够近”。
DBSCAN的独特之处
正如其名称所示,DBSCAN能够同时完成两项任务:
- 发现聚类
- 标记异常点(即不属于任何聚类的点)
这也解释了为何按此顺序介绍算法:
- K均值与高斯混合模型属于聚类模型,输出为紧凑对象:K均值输出质心,GMM输出均值与方差。
- 孤立森林与局部离群因子是纯粹的异常检测模型,其唯一目标是发现异常点。
- DBSCAN介于两者之间,基于邻域密度概念,同时实现聚类与异常检测。
使用小型数据集保持直观性
此处沿用局部离群因子算法中使用的小型数据集:1, 2, 3, 7, 8, 12。
观察这些数字,可以直观识别出两个紧凑的组:一组围绕1–2–3,另一组围绕7–8,而12则孤立存在。
DBSCAN算法恰好捕捉了这种直观结构。
三步总结DBSCAN
DBSCAN对每个点提出三个简单问题:
- 在给定小半径内,有多少邻居?
- 邻居数量是否达到成为核心点的阈值?
- 在识别核心点后,该点属于哪个连通组?
以下是DBSCAN算法的三步总结:
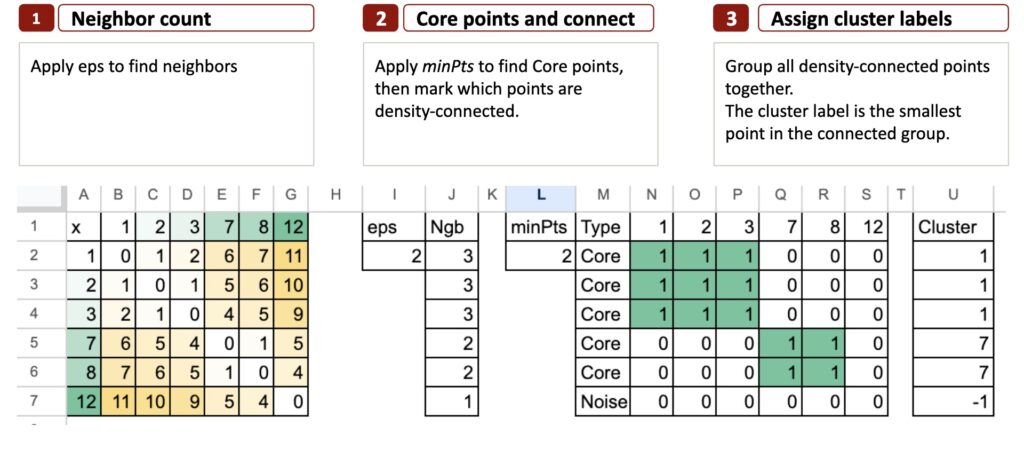
Excel中的DBSCAN – 所有图片由作者提供
接下来逐步解析。
DBSCAN的三个步骤
理解了密度与邻域的概念后,DBSCAN的描述变得非常简单。
整个算法流程可归纳为三个步骤。
步骤一:统计邻居数量
目标是检查每个点有多少邻居。
设定一个称为eps的小半径。
对于每个点,检查所有其他点,并标记距离小于eps的点。
这些点即为邻居。
由此获得密度的初步概念:
拥有众多邻居的点位于密集区域,
邻居稀少的点则位于稀疏区域。
对于当前的一维示例,常见设置为:
eps = 2
围绕每个点绘制半径为2的小区间。
为何称为eps?
名称eps源于希腊字母ε,在数学中传统上用于表示小量或点周围的小半径。
因此,在DBSCAN中,eps字面意为“小邻域半径”。
它回答了以下问题:
围绕每个点观察多远?
在Excel中,第一步是计算成对距离矩阵,然后统计每个点在eps内的邻居数量。

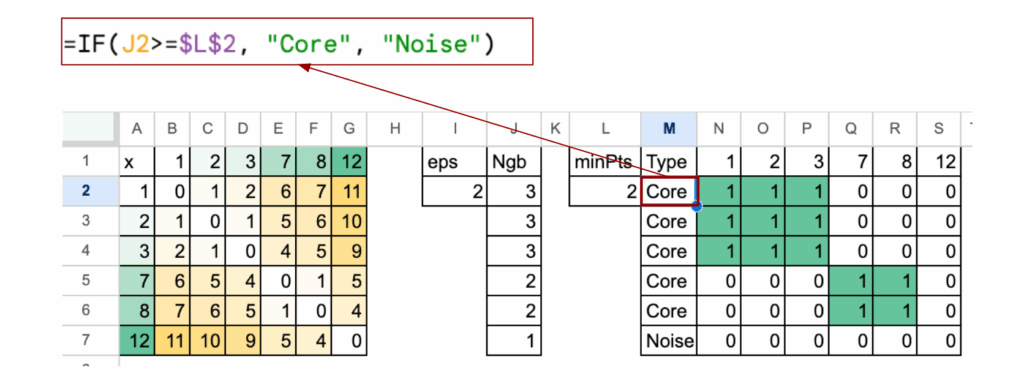
步骤二:核心点与密度连通性
在获得步骤一的邻居信息后,应用minPts参数决定哪些点是核心点。
minPts表示最小点数。
它是一个点被视为核心点所需的最小邻居数量(在eps半径内)。
如果一个点在eps内拥有至少minPts个邻居,则为核心点。
否则,它可能成为边界点或噪声点。
当eps = 2且minPts = 2时,点12不是核心点。
一旦识别出核心点,只需检查哪些点可以从它们密度可达。如果一个点可以通过在eps内从一个核心点移动到另一个核心点而到达,则属于同一组。
在Excel中,可以用简单的连通性表格表示,展示哪些点通过核心邻居相连。
DBSCAN利用这种连通性在步骤三中形成聚类。
步骤三:分配聚类标签
目标是将连通性转化为实际的聚类。
连通性矩阵准备就绪后,聚类自然显现。
DBSCAN简单地将所有连通点分组在一起。
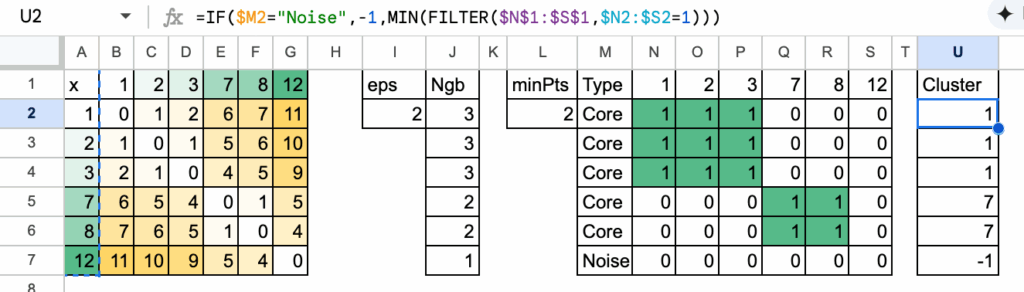
为每个组分配一个简单且可复现的名称,采用一个直观规则:
聚类标签是连通组中最小的点。
例如:
- 组 {1, 2, 3} 变为聚类 1
- 组 {7, 8} 变为聚类 7
- 像12这样没有核心邻居的点被标记为噪声
这正是将在Excel中使用公式展示的结果。
总结与思考
DBSCAN非常适合阐述局部密度的概念。
它不涉及概率、高斯公式或估计步骤。
仅依赖于距离、邻居和一个小半径。
但这种简单性也带来了局限性。
由于DBSCAN对所有点使用固定半径,当数据集中包含不同尺度的聚类时,它无法自适应调整。
HDBSCAN保留了相同的直觉,但考察所有半径并保留稳定的结构。
它更为鲁棒,更接近人类自然识别聚类的方式。
基于距离的无监督方法概览
通过DBSCAN,我们到达了一个回顾与总结已探索无监督模型的自然节点,同时也提及一些未涵盖的算法。
这是一个绘制小型图谱的好机会,将这些算法联系起来,并展示各自在更广阔领域中的位置。
- 基于距离的模型
K均值、K中心点和层次聚类通过比较点之间或组之间的距离来工作。
- 基于密度的模型
均值漂移和高斯混合模型估计平滑密度并从其结构中提取聚类。
- 基于邻域的模型
DBSCAN、OPTICS、HDBSCAN和局部离群因子从局部连通性而非全局距离定义聚类和异常。
- 基于图的模型
谱聚类、Louvain和Leiden依赖于相似性图内部的结构。
每组反映了对“聚类”是什么的不同哲学理解。
算法的选择往往较少取决于理论,而更多取决于数据的形状、密度的尺度以及期望发现的结构类型。
以下是这些方法之间的关联:
- 当用概率密度替换硬分配时,K均值可推广为GMM。
- 当消除对单一eps值的需求时,DBSCAN可推广为OPTICS。
- OPTICS自然地导向HDBSCAN,后者将密度连通性转化为稳定的层次结构。
- 层次聚类和谱聚类都基于成对距离构建聚类,但谱聚类增加了基于图的视角。
- 局部离群因子使用与DBSCAN相同的邻域概念,但仅用于异常检测。
虽然存在更多模型,但这提供了该领域的概览以及DBSCAN在其中的位置。
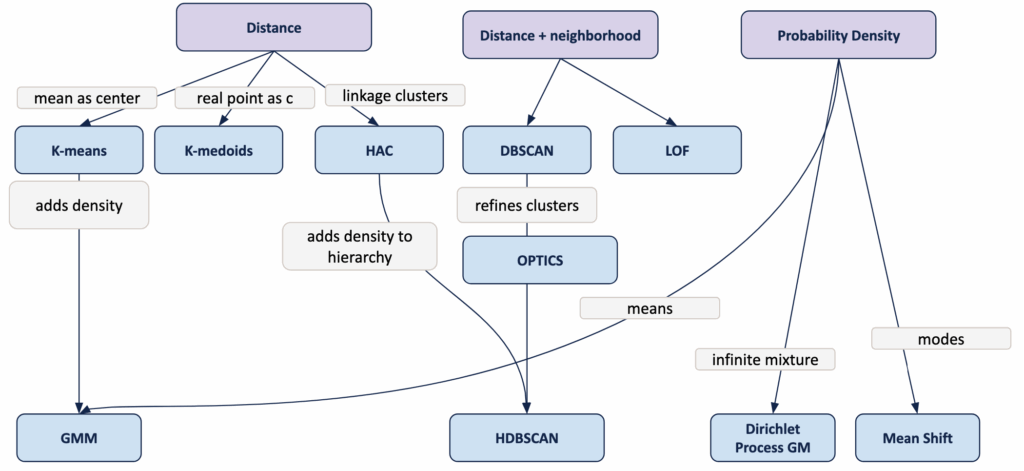
基于距离的无监督学习领域图谱 – 图片由作者提供
明天,我们将继续“降临日历”系列,介绍更“经典”且在日常机器学习中广泛使用的模型。