机器学习“倒数日历”第12天：在Excel中理解逻辑回归

今天要探讨的模型是逻辑回归。

如果已经对这个模型有所了解，可以先思考一个问题：

逻辑回归究竟是一个回归器，还是一个分类器？

这个问题就像在问：番茄是水果还是蔬菜？

从植物学家的角度看，番茄是水果，因为他们关注的是结构：种子、花朵和植物生物学特性。

从厨师的角度看，番茄是蔬菜，因为他们关注的是口味、在食谱中的用途，以及它是用于沙拉还是甜点。

同一个事物，两种答案都成立，关键在于视角不同。

逻辑回归的情况与此完全一致。

• 从统计学/广义线性模型（GLM）的视角看，它是一种回归。在这个框架下，甚至没有“分类”这个概念，只有伽马回归、逻辑回归、泊松回归等。
• 从机器学习的视角看，它被用于分类任务，因此它是一个分类器。

稍后会再回到这个话题。

目前可以确定的是：

当目标变量是二元的，并且通常编码为0或1时，逻辑回归非常适用。

但是……

基于权重的模型如何进行分类？

目标变量y可以是0或1。

0和1都是数字，对吗？

那么，是否可以将y视为连续变量来处理呢？

是的，可以尝试用y = a x + b这样的线性方程来拟合y=0或1的情况。

这有何不可？

现在可能会问：为什么现在才提出这个问题？之前为什么没有？

原因在于，对于基于距离和基于树的模型，分类变量y是真正意义上的类别。

当y是分类变量时，例如红色、蓝色、绿色，或者简单的0和1：

• 在K近邻（K-NN）中，通过查看每个类别的邻居进行分类。
• 在质心模型中，通过与每个类别的质心进行比较来分类。
• 在决策树中，在每个节点计算类别的比例。

在所有这些模型中：

类别标签不是数字。

它们是类别。

算法从不将它们视为数值。

因此，分类是自然而直接的。

但对于基于权重的模型，情况则不同。

在基于权重的模型中，通常计算的是类似：

y = a x + b

或者更复杂的带系数的函数。

这意味着：

模型在所有环节都处理数字。

因此，关键思路在于：

如果一个模型能做回归，那么它也可以用于二元分类。

是的，线性回归也可以用于二元分类！

因为二元标签0和1本身就是数值。

在这种特殊情况下：可以直接在y=0和y=1上应用普通最小二乘法（OLS）。

模型会拟合一条直线，并且可以使用与线性回归相同的闭式解公式，如下图所示。

逻辑回归在Excel中的实现 – 所有图片由作者提供

同样可以进行梯度下降，并且效果良好：

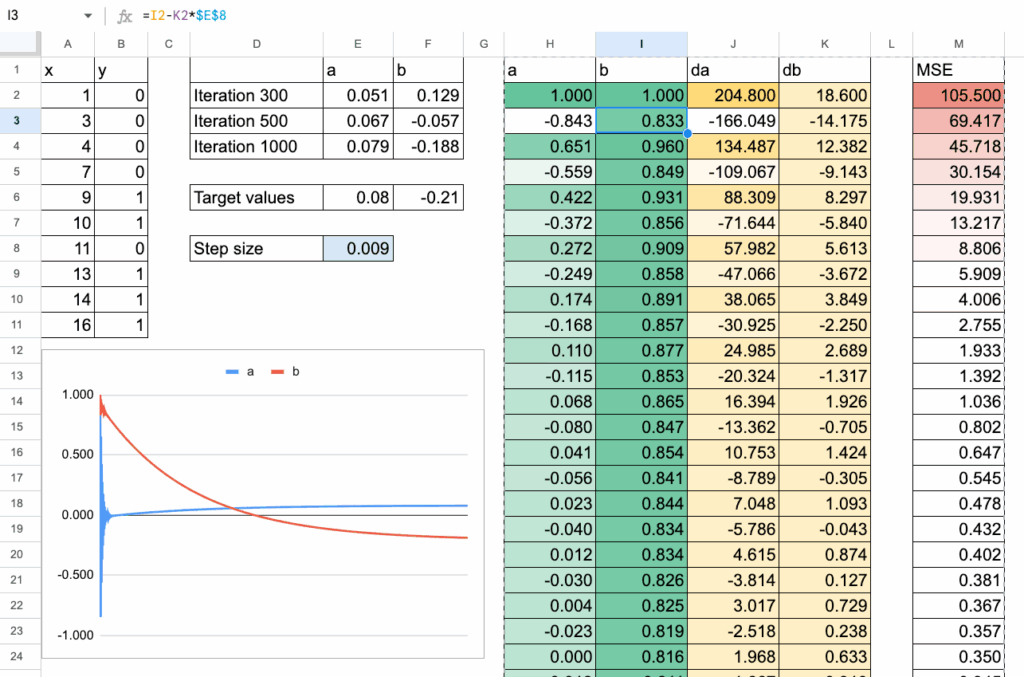
然后，为了获得最终的类别预测，只需选择一个阈值。

通常阈值设为0.5（或50%），但根据对严格程度的要求，也可以选择其他值。

• 如果预测的y≥0.5，则预测为类别1
• 否则，预测为类别0

这就构成了一个分类器。

由于模型产生的是数值输出，甚至可以找出y=0.5的点。

这个x值定义了决策边界。

在前面的例子中，这发生在x=9处。

在这个阈值下，已经可以看到一个错误分类。

但一旦引入一个具有较大x值的点，问题就出现了。

例如，假设添加一个点：x=50，y=1。

因为线性回归试图用一条直线拟合所有数据，这个大的x值会将直线向上拉。

决策边界从x=9左右移动到了大约x=12。

现在，有了这个新的边界，最终导致了两个错误分类。

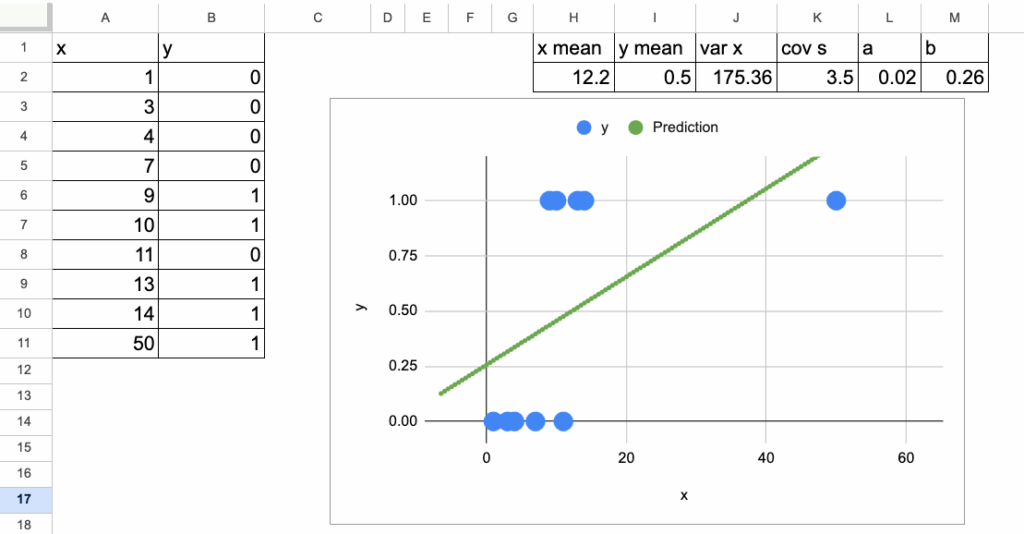
这说明了主要问题：

将线性回归用作分类器时，对x的极端值极其敏感。决策边界会发生剧烈移动，导致分类结果不稳定。

这就是为什么需要一个不会永远呈线性变化的模型。一个即使x变得非常大，预测值也能保持在0和1之间的模型。

而逻辑函数恰好能提供这种特性。

逻辑回归的工作原理

从线性部分开始：ax + b，与线性回归相同。

然后应用一个称为Sigmoid或逻辑函数的函数。

如下面的截图所示，p的值被限制在0和1之间，因此非常理想。

• p(x)是y = 1的预测概率
• 1 − p(x)是y = 0的预测概率

对于分类，可以简单地设定：

• 如果p(x) ≥ 0.5，预测类别1
• 否则，预测类别0

从似然到对数损失

线性回归的OLS方法试图最小化均方误差（MSE）。

对于二元目标变量的逻辑回归，使用的是伯努利似然。对于每个观测i：

• 如果yᵢ = 1，该数据点的概率是pᵢ
• 如果yᵢ = 0，该数据点的概率是1 − pᵢ

对于整个数据集，似然是所有i的乘积。实践中，通常取对数，将乘积转化为求和。

在GLM视角下，目标是最大化这个对数似然。

在机器学习视角下，将损失定义为负的对数似然，并对其进行最小化。这就得到了常用的对数损失（log-loss）。

两者是等价的。此处不展开证明。

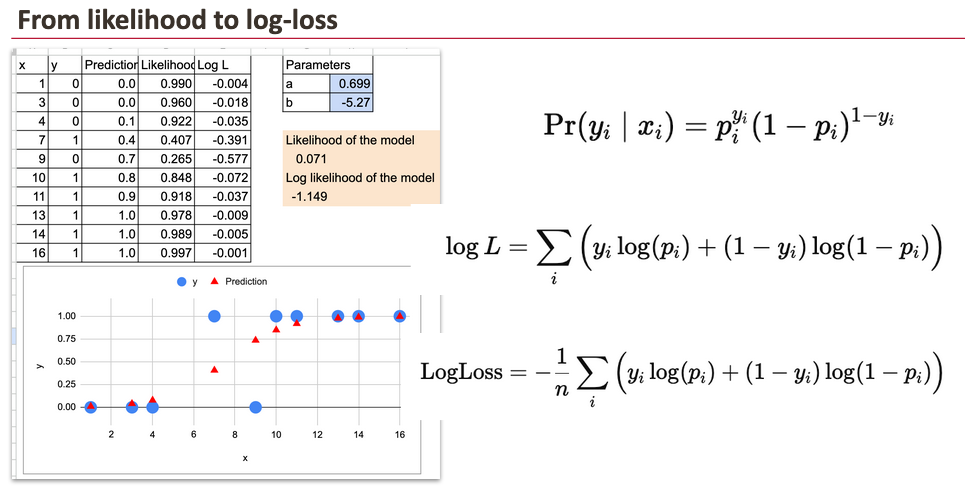
逻辑回归的梯度下降

原理

就像在线性回归中所做的那样，这里也可以使用梯度下降。其思想始终相同：

1. 从a和b的某个初始值开始。
2. 计算损失及其关于a和b的梯度（导数）。
3. 将a和b向减小损失的方向移动一小步。
4. 重复上述步骤。

并无神秘之处。

只是与之前相同的机械过程。

步骤1. 梯度计算

对于逻辑回归，平均对数损失的梯度遵循一个非常简单的结构。

本质上就是平均残差。

下面仅给出可以在Excel中实现的公式结果。可以看到，尽管对数损失公式初看可能复杂，但最终形式相当简单。

Excel可以通过简单的SUMPRODUCT公式计算这两个量。

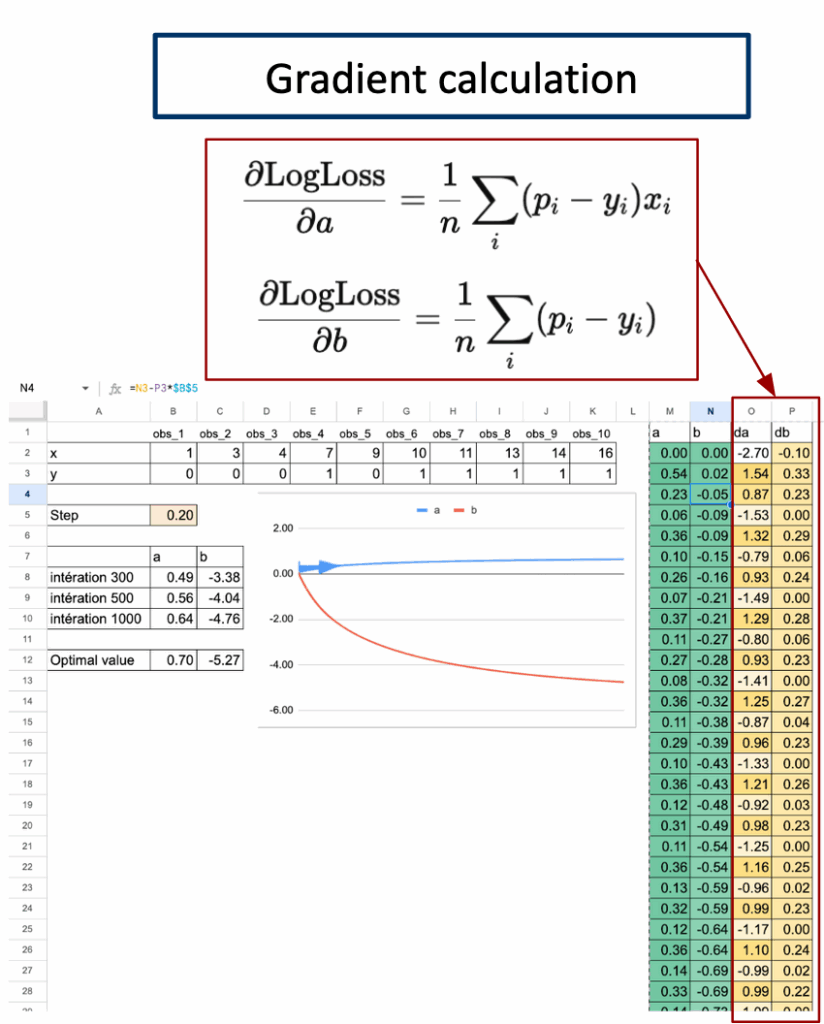
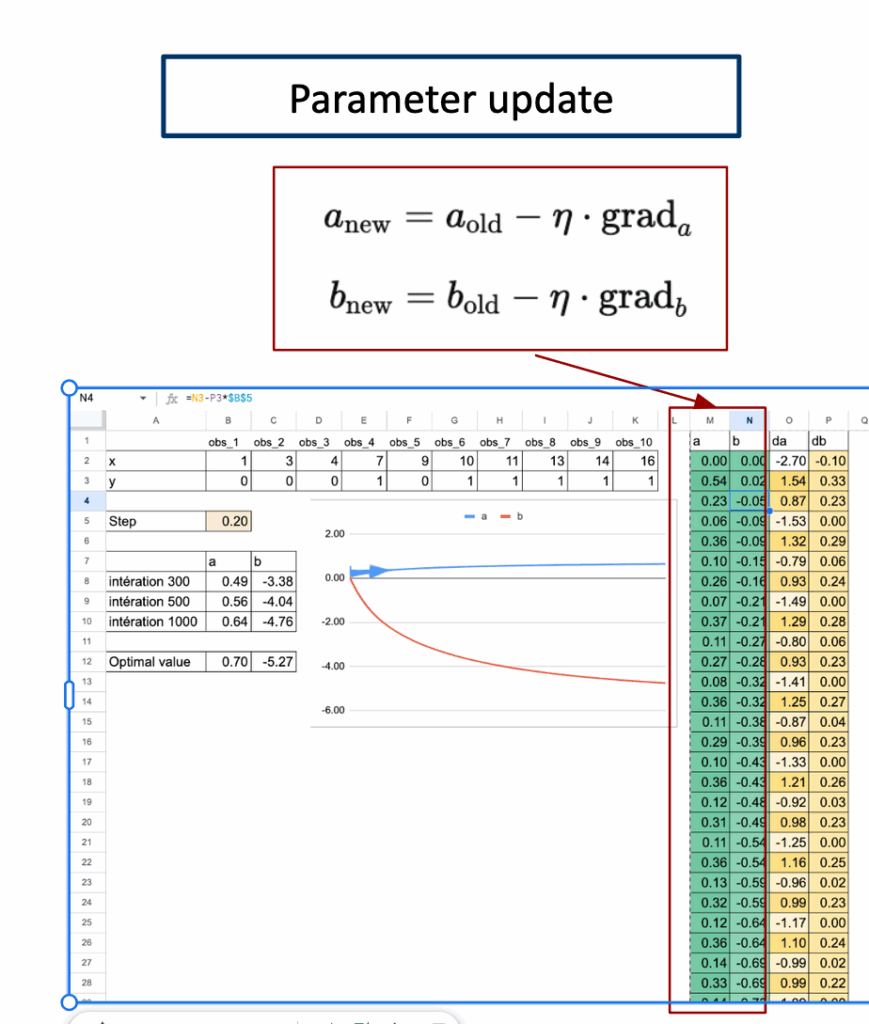
步骤2. 参数更新

一旦计算出梯度，就可以更新参数。

这个更新步骤在每次迭代中重复。

随着迭代的进行，损失下降，参数收敛到最优值。

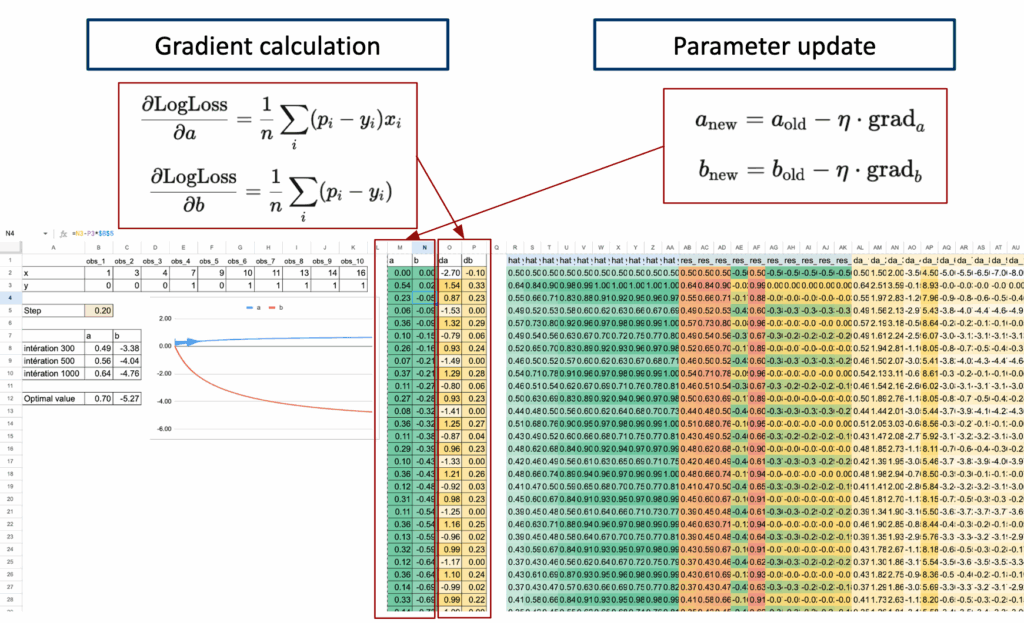
至此，整个流程已清晰呈现。

可以看到模型、损失、梯度和参数更新的全貌。

借助Excel中每次迭代的详细视图，实际上可以操作模型：改变一个值，观察曲线移动，并逐步看到损失下降。

观察所有部分如何清晰地组合在一起，会带来令人惊讶的满足感。

多类别分类怎么办？

对于基于距离和基于树的模型：

完全没有问题。

它们天然地处理多个类别，因为它们从不将标签解释为数字。

但对于基于权重的模型呢？

这里就遇到了问题。

如果为类别分配数字：1、2、3等。

那么模型会将这些数字解释为真实的数值。

这将导致一系列问题：

• 模型会认为类别3比类别1“更大”
• 类别1和类别3之间的中点是类别2
• 类别之间的距离变得有意义

但在分类任务中，这些都不是真实的。

因此：

对于基于权重的模型，不能简单地使用y = 1, 2, 3来进行多类别分类。

这种编码方式是不正确的。

后续将探讨如何解决这个问题。

结论

从一个简单的二元数据集出发，探讨了基于权重的模型如何充当分类器，线性回归为何很快达到其极限，以及逻辑函数如何通过将预测值限制在0和1之间来解决这些问题。

然后，通过似然和对数损失来表达模型，得到了一个既数学严谨又易于实现的公式。

一旦所有内容都在Excel中构建完成，整个学习过程就变得可见：概率、损失、梯度、更新，以及最终参数的收敛。

借助详细的迭代表格，可以实际看到模型是如何一步步改进的。

可以改变一个值、调整学习率或添加一个点，并立即观察到曲线和损失如何反应。

这就是在电子表格中进行机器学习的真正价值：没有任何隐藏，每个计算都是透明的。

通过这种方式构建逻辑回归，不仅能理解模型，更能理解它为何如此训练。