逻辑回归可用于处理二分类问题。那么,当类别数量超过两个时,又该如何应对呢?
Softmax回归正是这一思路向多类别场景的自然延伸。在“机器学习倒数日历”系列的第14天,将探讨这一模型。
与逻辑回归只生成一个分数不同,Softmax回归会为每个类别生成一个分数。随后,通过应用Softmax函数,将这些分数转化为一组总和为1的概率值。
理解Softmax模型
在训练模型之前,首先需要理解模型本身的运作机制。Softmax回归的第一步并非优化,而是理解预测是如何计算的。
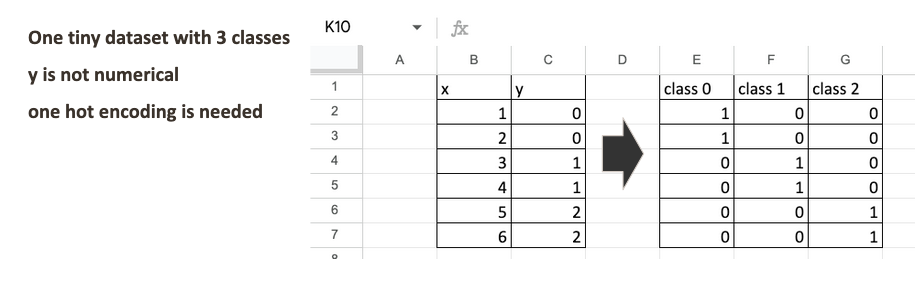
一个包含3个类别的微型数据集
假设有一个小型数据集,包含一个特征x和三个类别。目标变量y不应被视为数值,它代表的是类别而非数量。一种常见的表示方法是独热编码,即每个类别由其自身的指示符表示。
从这个角度看,Softmax回归可以看作是三个并行运行的逻辑回归模型,每个对应一个类别。小型数据集非常适合学习,可以清晰地看到每个公式、每个数值,以及模型的每个部分如何贡献于最终结果。
Excel中的Softmax回归 – 所有图片由作者提供
模型描述
那么,模型具体是什么?
每个类别的分数
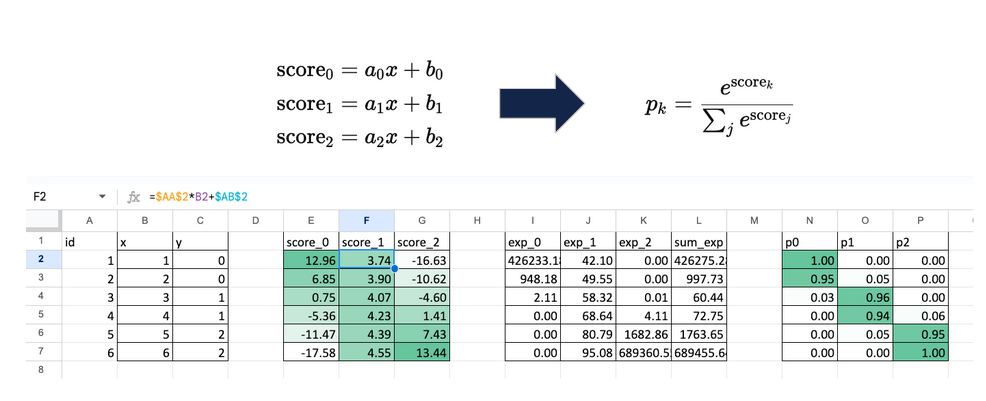
在逻辑回归中,模型分数是一个简单的线性表达式:分数 = a * x + b。Softmax回归做的是完全相同的事情,但为每个类别生成一个分数:
分数_0 = a0 * x + b0
分数_1 = a1 * x + b1
分数_2 = a2 * x + b2
在此阶段,这些分数只是实数,还不是概率。
将分数转化为概率:Softmax步骤
Softmax函数将三个分数转化为三个概率。每个概率均为正数,且三者之和为1。计算过程直接明了:
- 对每个分数取指数
- 计算所有指数值的总和
- 将每个指数值除以该总和
由此得到每行数据对应的p0、p1和p2。这些值代表了模型对每个类别的置信度。至此,模型已完全定义。训练模型将仅涉及调整系数ak和bk,以使这些概率尽可能匹配观测到的类别。
Excel中的Softmax回归 – 所有图片由作者提供
可视化Softmax模型
模型完全定义后,包含:每个类别的一个线性分数,以及一个将这些分数转化为概率的Softmax步骤。训练模型仅涉及调整系数ak和bk,以使这些概率尽可能匹配观测到的类别。
一旦找到系数,就可以可视化模型的行为。为此,取一个输入值范围,例如x从0到7,然后计算:分数0、分数1、分数2以及相应的概率p0、p1、p2。绘制这些概率会得到三条平滑曲线,每条对应一个类别。
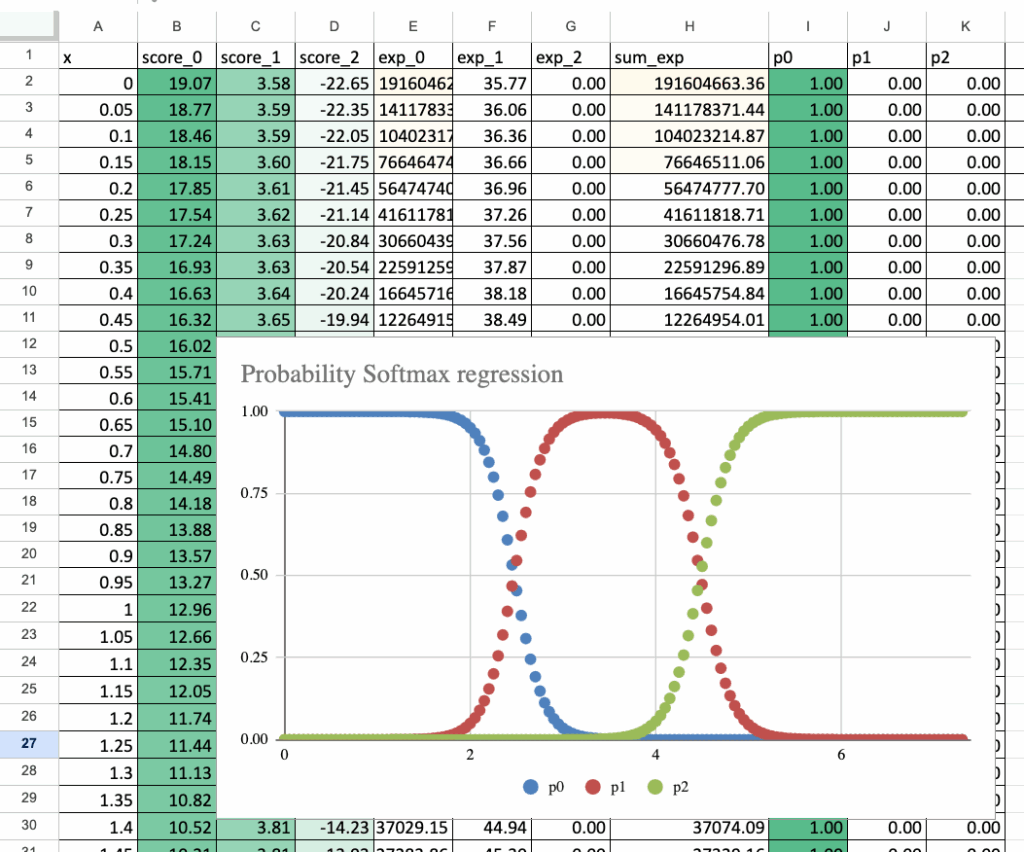
Excel中的Softmax回归 – 所有图片由作者提供
结果非常直观。对于较小的x值,类别0的概率较高。随着x增加,此概率下降,而类别1的概率上升。对于更大的x值,类别2的概率占据主导。在每个x值处,三个概率之和均为1。模型不做突然的决策,而是表达对每个类别的置信程度。
此图使Softmax回归的行为易于理解:可以看到模型如何平滑地从一类过渡到另一类;决策边界对应于概率曲线的交点;模型逻辑变得可见而非抽象。这是在Excel中构建模型的关键优势之一:不仅能计算预测,还能看到模型的“思考”过程。
交叉熵损失与梯度下降
模型定义后,需要一种方法来评估其好坏,以及一种改进其系数的方法。这两个步骤都重用了逻辑回归中已有的思想。
评估模型:交叉熵损失
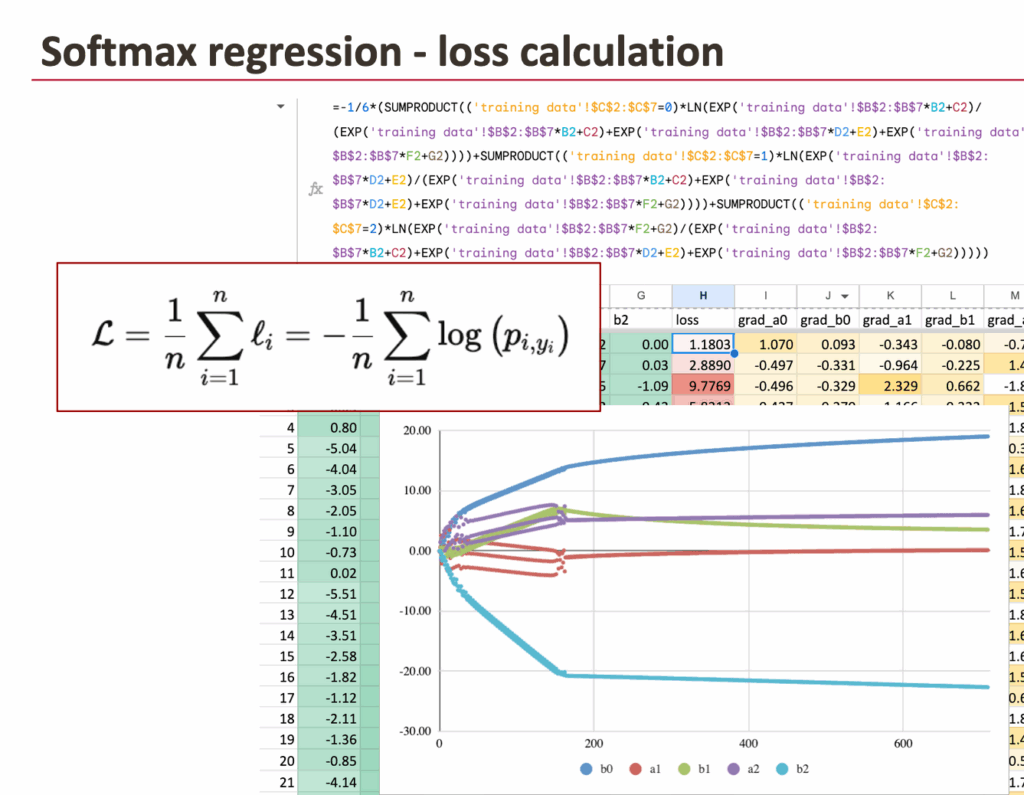
Softmax回归使用与逻辑回归相同的损失函数。对于每个数据点,查看分配给正确类别的概率,并取其负对数:损失 = – log (p_真实类别)。如果模型为正确类别分配高概率,则损失小;如果分配低概率,则损失大。
在Excel中,这很容易实现。根据y的值选择正确的概率,并应用对数函数:损失 = -LN( CHOOSE(y + 1, p0, p1, p2) )。最后,计算所有行的平均损失。这个平均损失正是需要最小化的量。
Excel中的Softmax回归 – 所有图片由作者提供
计算残差
为了更新系数,首先计算每个类别的残差。对于每一行:
- 如果y等于0,则残差_0 = p0 – 1,否则为 p0 – 0
- 如果y等于1,则残差_1 = p1 – 1,否则为 p1 – 0
- 如果y等于2,则残差_2 = p2 – 1,否则为 p2 – 0
换句话说,对于正确类别,减去1;对于其他类别,减去0。这些残差衡量了预测概率与期望值之间的差距。
计算梯度
梯度通过将残差与特征值结合得到。对于每个类别k:
- ak的梯度是
残差_k * x的平均值 - bk的梯度是
残差_k的平均值
在Excel中,这可以通过简单的公式如SUMPRODUCT和AVERAGE来实现。至此,一切都是显式的:可以看到残差、梯度以及每个数据点的贡献。
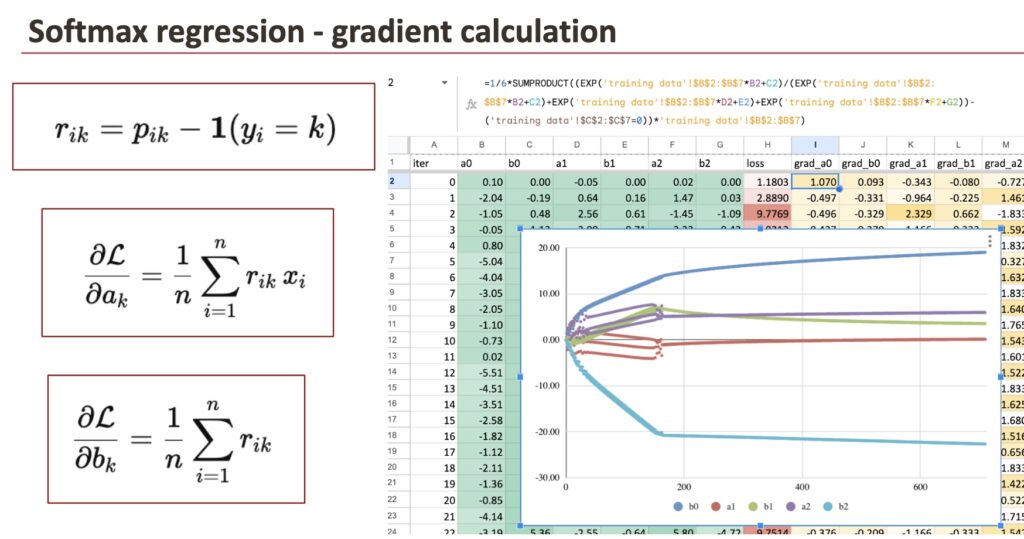
更新系数
一旦梯度已知,就使用梯度下降法更新系数。这一步与之前在逻辑回归或线性回归中看到的完全相同。唯一的区别是现在需要更新六个系数,而不是两个。
为了可视化学习过程,可以创建一个新工作表,每行代表一次迭代:当前迭代编号、六个系数(a0, b0, a1, b1, a2, b2)、损失值以及梯度。第2行对应迭代0,包含初始系数。第3行使用第2行的梯度计算更新后的系数。将公式向下拖动数百行,即可模拟多次迭代的梯度下降过程。
由此可以清晰地看到:系数逐渐稳定;损失值迭代后不断下降。这使得学习过程变得具体可感。无需想象优化器,可以直接观察模型的学习过程。

逻辑回归作为Softmax回归的特例
逻辑回归和Softmax回归常被呈现为不同的模型。实际上,它们是同一思想在不同尺度上的体现。Softmax回归为每个类别计算一个线性分数,并通过比较这些分数将其转化为概率。当只有两个类别时,这种比较仅取决于两个分数之间的差值。这个差值是输入的线性函数,在这种情况下应用Softmax恰好产生逻辑(Sigmoid)函数。
换言之,逻辑回归只是应用于两个类别的Softmax回归,并移除了冗余参数。一旦理解了这一点,从二分类扩展到多分类就成为一个自然的延伸,而非概念上的跳跃。

结论
Softmax回归并未引入新的思维方式。它仅仅表明,逻辑回归已经包含了所需的一切。通过为每个类别复制线性分数并用Softmax进行归一化,可以在不改变底层逻辑的情况下,从二元决策转向多类别概率。
损失函数是相同的思路。梯度具有相同的结构。优化过程是已知的相同梯度下降法。唯一改变的是并行分数的数量。
处理多分类问题的另一种方法?
Softmax并非基于权重的模型中处理多类问题的唯一方式。还有另一种方法,概念上不那么优雅,但在实践中非常常见:一对多或一对一分类。不是构建单一的多类模型,而是训练多个二元模型并组合它们的结果。这种策略在支持向量机中被广泛使用。






