在管理复杂的业务逻辑时,嵌套的if-else语句常常如同迷宫一般,令人难以理清头绪,极易迷失。面对任务关键型场景,例如形式验证或可满足性问题,许多开发者倾向于使用自动化定理证明器或SMT求解器等复杂工具。然而,这些强大的方法有时可能过于复杂,并且实现起来令人头疼。如果只需一个简单、透明的规则引擎,又该如何构建呢?
构建这样一个轻量级引擎的关键思想,源于一个曾被认为是深刻但并不实用的概念:真值表。其致命缺陷在于指数级增长,这使得它们似乎不适用于解决实际问题。至少,过去人们普遍是这样认为的。
一个简单的观察改变了这一切:在几乎所有实际应用场景中,那些“大到不可能”的真值表实际上并非信息密集型;它们本质上是伪装的稀疏矩阵。
这一全新的视角让真值表在概念上更加清晰,在计算上更具可行性。
本文将展示如何将这一洞察转化为一个轻量且功能强大的规则引擎。文章将引导读者逐步完成从零开始构建该引擎所需的所有步骤。此外,读者也可以直接使用开源库 vector-logic,立即开始构建应用程序。本教程将提供所有必要的细节,以帮助理解其内部工作原理。
虽然所有的理论背景和数学细节都可以在关于状态代数的研究论文[1]中找到,但本文将侧重于实际应用。接下来,将深入探讨构建过程!
逻辑学基础回顾
真值表
首先回顾一下基础知识:逻辑公式是由布尔变量和逻辑连接词(如AND、OR、NOT)构建的表达式。在实际应用中,布尔变量可以代表事件(例如,“咖啡杯满了”这一事件,如果杯子实际是满的则为真,否则为假)。例如,公式 f=(x 1∨x 2) 在 x 1 为真、x 2 为真或两者都为真时成立。利用这个框架,可以构建一个包含所有可能现实的详尽穷举映射——即真值表。
将“真”表示为1,“假”表示为0,x 1∨x 2 的真值表如下所示:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪x 1 0 0 1 1 x 2 0 1 0 1 x 1∨x 2 0 1 1 1⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪
进行逻辑推理所需的一切都编码在真值表中。接下来,将通过实例进行演示。
逻辑推理
考虑一个经典的蕴涵传递性例子。假设已知… 顺便一提,所有被“已知”的信息都称为前提。假设有两个前提:
- 如果 x 1 为真,那么 x 2 必须为真 (x 1→x 2)
- 如果 x 2 为真,那么 x 3 必须为真 (x 2→x 3)
很容易猜测出结论:“如果 x 1 为真,那么 x 3 必须为真” (x 1→x 3)。然而,可以使用真值表给出形式化的证明。首先对这些公式进行标记:
f 1=(x 1→x 2)f 2=(x 2→x 3)f 3=(x 1→x 3)前提 1 前提 2 结论
第一步是构建一个真值表,涵盖三个基本变量 x 1、x 2 和 x 3 的所有组合:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪x 1 0 0 0 0 1 1 1 1 x 2 0 0 1 1 0 0 1 1 x 3 0 1 0 1 0 1 0 1 f 1 1 1 1 1 0 0 1 1 f 2 1 1 0 1 1 1 0 1 f 3 1 1 1 1 0 1 0 1⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪
此表包含八行,对应于基本变量的每一种真值赋值。变量 f 1、f 2 和 f 3 是派生的,其值直接从 x 变量计算得出。
即使是这种简单情况,表格的规模也相当可观!
下一步是将由 f 1 和 f 2 表示的前提作为现实的过滤器。已知这两个前提都为真。因此,任何 f 1 或 f 2 为假的行都代表不可能的场景,应予舍弃。
应用此过滤器后,将得到一个显著缩小的表格:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪x 1 0 0 0 1 x 2 0 0 1 1 x 3 0 1 1 1 f 1 1 1 1 1 f 2 1 1 1 1 f 3 1 1 1 1⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪
由此可见:在每个剩余的有效场景中,f 3 都为真。这证明了 f 3 逻辑上必然从 f 1 和 f 2 推导(或蕴涵)而出。
这确实是一种优雅直观的方法。那么,为什么它不常用于复杂系统呢?答案在于简单的数学:仅有三个变量时,真值表有 2 3=8 行。若有 20 个变量,行数将超过一百万。若变量数量达到 200,行数将超过太阳系中的原子数量。不过,文章并非在此止步。这个问题是可以解决的。
稀疏表示
解决真值表指数级增长问题的核心思想在于采用一种能够实现无损压缩的紧凑表示。
除了压缩真值表,还需要一种高效的方法来进行逻辑推理。通过引入“状态向量”(代表一组状态,即真值表的行),并采用集合论操作(如并集和交集)来操纵它们,可以实现这一目标。
压缩真值表
首先,回到公式 f=(x 1→x 2)。找出使该公式为真的行。使用符号 ∼ 来表示公式与其“有效”真值赋值表之间的对应关系。在 f 的蕴涵示例中,可以这样表示:
f∼⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪x 1 0 0 1 x 2 0 1 1⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪
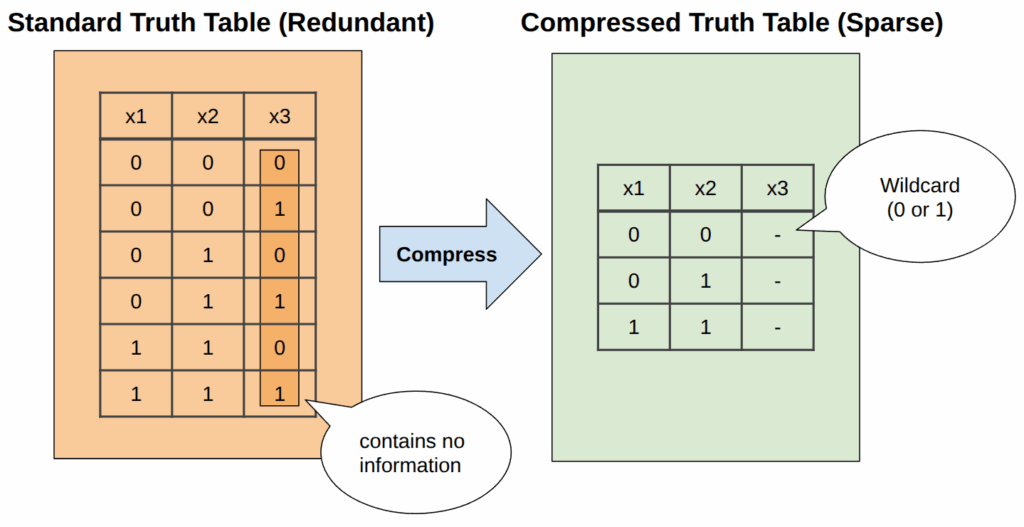
请注意,由于行 (1,0) 使 f 无效,因此将其舍弃。如果现在将此表扩展,使其包含 f 不依赖的第三个变量 x 3,会发生什么?经典方法会将真值表的大小加倍,以考虑 x 3 为 0 或 1 的情况,尽管这并没有为 f 增加任何新信息:
f∼⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪x 1 0 0 0 0 1 1 x 2 0 0 1 1 1 1 x 3 0 1 0 1 0 1⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪
这简直是浪费!无信息列可以被压缩,为此,引入了一个破折号 (–) 作为“通配符”符号。可以将其视为一个逻辑上的薛定谔猫:该变量处于 0 和 1 的叠加态,直到一个约束或一次测量(在学习的语境中,称之为“证据”)将其强制进入一个确定的状态,从而消除其中一种可能性。
现在,可以在 n 个变量的宇宙中表示 f,而不会产生任何冗余:
f∼⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪x 1 0 0 1 x 2 0 1 1 x 3–––…………x n−––⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪
可以将其泛化,即假设任何包含破折号的行都等同于通过将破折号替换为所有可能的 0 和 1 组合而获得的多行集合。例如(可以尝试用纸笔推导一下!):
⎧⎩⎨⎪⎪⎪⎪x 1––x 2 0 1 x 3–1⎫⎭⎬⎪⎪⎪⎪=⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪x 1 0 0 1 1 0 1 x 2 0 0 0 0 1 1 x 3 0 1 0 1 1 1⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪
这就是稀疏表示的精髓所在。接下来介绍一些基本操作的定义:将破折号替换为 0 和 1 的过程称为展开(expansion)。相反地,识别模式并引入破折号的过程称为规约(reduction)。最简单的规约形式,即用一行替换两行,称为原子规约(atomic reduction)。
状态代数
现在,为这些概念赋予一些结构。
- 一个状态(state)是对所有变量的单一、完整的真值赋值——在完全展开的真值表中就是一行(例如 (0,1,1))。
- 一个状态向量(state vector)是状态的集合(可以将其视为真值表的一个子集)。一个逻辑公式现在可以被视为一个状态向量,其中包含所有使该公式为真的状态。特殊情况包括空状态向量 (0) 和一个包含所有 2 n 种可能状态的向量,后者被称为平凡(trivial)向量,并表示为 t。(正如即将看到的,这对应于一个包含所有通配符的 t-对象。)
- 状态向量紧凑表示中的一行(例如 (0,−,1))被称为t-对象(t-object)。它是基本构建块——一个可以代表一个或多个状态的模式。
概念上,将焦点从表格转向集合是关键一步。回想一下,使用真值表方法进行推理时:将前提 f 1 和 f 2 用作过滤器,只保留两个前提都为真的行。这一操作,用集合论的语言来说,就是交集。
每个前提都对应一个状态向量(满足该前提的状态集合)。组合知识的状态向量是这些前提向量的交集。此操作是新模型的核心。
为了更友好的表示,引入了一些“语法糖”,将集合操作映射到简单的算术操作:
- 集合并集 (∪) → 加法 (+)
- 集合交集 (∩) → 乘法 (∗)
这些操作的属性(结合律、交换律和分配律)允许使用高中代数符号来表示涉及集合操作的复杂表达式:
(A∪B)∩(C∪D)=(A∩C)∪(A∩D)∪(B∩C)∪(B∩D)→(A+B)⋅(C+D)=A C+A D+B C+B D
回顾一下当前进展。已经为新框架奠定了坚实基础。真值表现在以稀疏形式表示,并被重新解释为集合(状态向量)。还确立了逻辑推理可以通过状态向量的乘法来实现。
距离目标已近。但在将此理论应用于开发高效推理算法之前,还需要一个关键要素。接下来,更深入地研究 t-对象上的操作。
核心机制:T-对象上的操作
现在,已准备好进入下一阶段——创建一个代数引擎来高效操纵状态向量。构建的基础是 t-对象——它是一种紧凑、基于通配符的状态向量单行表示形式。
请注意,要描述一行,只需知道 0 和 1 的位置。将一个 t-对象表示为 t α β,其中 α 是变量为 1 的索引集合,β 是变量为 0 的索引集合。例如:
{x 1 1 x 2 0 x 3–x 4 1}=t 14 2
一个由所有破折号组成的 t-对象 t={−–…−} 表示前面提及的、包含所有可能状态的平凡状态向量。
从公式到 T-对象
状态向量是其行的并集,或者用新符号表示,是其 t-对象的和。这被称为行分解(row decomposition)。例如,公式 f=(x 1→x 2) 可以表示为:
f∼⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪x 1 0 0 1 x 2 0 1 1…………x n−––⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪=t 12+t 2 1+t 12
值得注意的是,即使向系统中添加更多变量 (x 3,x 4,…),这种分解也不会改变,这表明该方法本身具有可扩展性。
矛盾法则
同一个索引不能同时出现在 t-对象的上标和下标位置。如果发生这种情况,t-对象将是空的(一个空集)。例如(冲突的索引已高亮显示):
t 1 3 2 3=0
这在代数上等同于逻辑矛盾。一个变量(在本例中为 x 3)不能同时为真(上标)和为假(下标)。任何此类 t-对象都代表不可能的状态,因此会消失。
简化表达式:原子规约
原子规约可以使用新引入的 t-对象符号清晰地表达。如果两行除了一个变量外完全相同(该变量在一个行中为 0,在另一行中为 1),那么这两行可以被规约。例如:
⎧⎩⎨⎪⎪⎪⎪x 1 1 1 x 2––x 3 0 0 x 4 0 1 x 5––⎫⎭⎬⎪⎪⎪⎪={x 1 1 x 2–x 3 0 x 4–x 5–}
用代数术语来说,这便是:
t 1 34+t 14 3=t 1 3
此操作的规则直接源于 t-对象的定义:如果两个 t-对象的索引集合除了一个索引(在一个 t-对象中是上标,在另一个中是下标)外完全相同,它们便会合并。冲突的索引(本例中的 4)被消除,两个 t-对象融为一体。
通过应用原子规约,可以简化公式 f=(x 1→x 2) 的分解。注意到 t 12+t 2 1=t 1,从而得到:
f∼t 12+t 2 1+t 12=t 1+t 12
核心操作:乘法
最后,讨论规则引擎最重要的操作:交集(在集合论中),表示为乘法(在代数中)。如何找到两个 t-对象共有的状态?
控制此操作的规则非常直接:要将两个 t-对象相乘,只需形成它们上标的并集以及下标的并集(此处将证明留给好奇的读者作为简单练习):
t α 1 β 1 t α 2 β 2=t α 1∪α 2 β 1∪β 2
矛盾法则依然适用。如果结果的上标和下标集合重叠,则乘积消失:
t α 1∪α 2 β 1∪β 2=0⟺(α 1∪α 2)∩(β 1∪β 2)≠∅
例如:
t 12 34 t 5 6=t 125 346 t 12 34 t 4=t 12 4 3 4=0 简单组合 消失,因为 4 同时存在于两个集合中
乘积的消失意味着两个 t-对象没有共同的状态;因此,它们的交集为空。
这些规则完成了整个构建过程。定义了逻辑的稀疏表示以及用于操作这些对象的代数。这些便是所需的所有理论工具。现在已准备好将它们组装成一个实用的算法。
融会贯通:状态代数推理实践
引擎已准备就绪,是时候启动它了!其核心思想很简单:要找到有效状态的集合,需要将所有对应于前提和证据的状态向量相乘。
如果有两个前提,分别由状态向量 (t(1)+t(2)) 和 (t(3)+t(4)) 表示,那么两者都为真的状态集合是它们的乘积:
(t(1)+t(2))(t(3)+t(4))=t(1)t(3)+t(1)t(4)+t(2)t(3)+t(2)t(4)
此示例可以轻松推广到任意数量的前提和 t-对象。
推理算法非常直接:
- 分解:将每个前提转换为其状态向量表示(t-对象的和)。
- 简化:对每个状态向量使用原子规约,使其尽可能紧凑。
- 相乘:将所有前提的状态向量相乘。结果是一个单一的状态向量,代表与所有前提一致的所有状态。
- 再次规约:最终乘积可能仍有可规约项,因此再次进行简化。
示例:代数方式证明传递性
回顾经典的蕴涵传递性例子:如果 f 1=(x 1→x 2) 和 f 2=(x 2→x 3) 为真,则证明 f 3=(x 1→x 3) 也必须为真。首先,按如下方式写出前提的简化状态向量:
f 1∼t 1+t 12 f 2∼t 2+t 23
为了证明这一结论,可以使用反证法。可以提出这样的问题:是否存在一个场景,其中前提为真,但结论 f 3 为假?
使 f 3=(x 1→x 3) 无效的状态是 x 1 为真 (1) 且 x 3 为假 (0) 的状态。这对应于一个单一的 t-对象:t 1 3。
现在,通过将所有元素相乘,验证这个“无效”状态向量是否能与前提共存:
(前提 1)×(前提 2)×(无效状态向量)(t 1+t 12)(t 2+t 23)t 1 3
首先,乘以无效的 t-对象,因为它是限制性最强的项:
(t 1 t 1 3+t 12 t 1 3)(t 2+t 23)=(t 1 1 3+t 12 3)(t 2+t 23)
第一项 t 1 1 3 由于矛盾而消失。因此,剩下:
t 12 3(t 2+t 23)=t 12 3 t 2+t 12 3 t 23=t 1 2 2 3+t 12 3 3=0+0=0
交集为空。这证明了不存在 f 1 和 f 2 为真但 f 3 为假的可能性。因此,f 3 必然从前提中推导而出。
反证法并非解决此问题的唯一途径。读者可在“状态代数”论文 [1] 中找到更详细的分析。
从逻辑谜题到欺诈检测
这不仅仅是关于逻辑谜题。当今世界很大一部分都由规则和逻辑所主导!例如,可以考虑一个基于规则的欺诈检测系统。
知识库是一组规则,例如:
IF card_location is overseas AND transaction_amount > $1000, THEN risk is high
整个知识库可以被编译成一个单一的大型状态向量。
现在,一笔交易发生。这就是证据:
card_location = overseas, transaction_amount > $1000, user_logged_in = false
此证据是一个单一的 t-对象,将 1 赋给已观察到的真事实,将 0 赋给假事实,并将所有未观察到的事实保留为通配符。
为了做出决策,只需简单地进行乘法运算:
知识库向量×证据 T-对象
由此产生的状态向量会立即告知目标变量(如 risk)在给定证据下的值。无需复杂的“if-then-else”语句链。
规模化:优化策略
与机械引擎类似,有许多方法可以提高该引擎的效率。
必须面对现实:逻辑推理问题在计算上是困难的,这意味着最坏情况下的运行时是非多项式的。简单来说,无论表示方式多么紧凑,或算法多么智能,在最坏情况下,运行时将极其漫长。漫长到很可能在结果计算出来之前就必须停止计算。
SAT 求解器表现出色的原因并非它们改变了现实。而是因为大多数现实问题并非最坏情况。在“平均”问题上的运行时,将对算法用于计算的启发式优化策略极其敏感。
因此,优化启发式算法可能是引擎实现有意义可扩展性的最重要组成部分之一。在此,仅暗示了可以考虑优化的可能之处。
请注意,当相乘多个状态向量时,中间 t-对象的数量在最终缩小之前可能会显著增长,但可以采取以下措施以确保引擎平稳运行:
- 持续规约:每次乘法运算后,对生成的状态向量运行规约算法。这能保持中间结果的紧凑性。
- 启发式排序:乘法运算的顺序很重要。通常,最好先乘以较小或限制性更强的状态向量,因为这可以使更多的 t-对象尽早消失,从而剪枝计算过程。
总结
本文带领读者探索了如何将命题逻辑转化为状态向量的形式,以便使用基本代数进行逻辑推理。这种方法的优雅之处在于其简洁性和高效性。
在任何环节,推理都不需要计算巨大的真值表。知识库被表示为一组稀疏矩阵(状态向量),逻辑推理被简化为一系列代数操作,这些操作可以通过几个直接的步骤实现。
虽然该算法并非旨在与尖端的 SAT 求解器和形式验证算法竞争,但它提供了一种优美、直观的方式,以高度紧凑的形式表示逻辑。它是构建轻量级规则引擎的强大工具,也是思考逻辑推理的优秀心智模型。
亲身体验
理解这个系统的最佳方式是亲自动手使用它。整个算法已封装成一个名为 vector-logic 的开源 Python 库。它可以直接从 PyPI 安装:
pip install vector-logic
完整的源代码,以及更多示例和文档,可在以下平台获取:
鼓励读者探索该仓库,尝试将其应用于自己的逻辑问题,并积极贡献。
如果对深入研究数学理论感兴趣,可以查阅原始论文 [1]。该论文涵盖了一些本文无法纳入的实践指南主题,例如规范规约、正交化等。它还基于 t-对象形式主义建立了命题逻辑的抽象代数表示。
欢迎任何意见或问题。