旋转位置编码(RoPE)原理解析
引言
现有的大量资源都在探讨Transformer架构,但旋转位置嵌入(RoPE)却往往被简单带过或完全忽略。RoPE最初发布于论文《RoFormer: Enhanced Transformer with Rotary Position Embedding》,虽然其数学运算主要涉及旋转矩阵和矩阵乘法,但理解其运作原理才是关键挑战。
RoPE的直觉理解
Transformer缺乏对顺序和距离的内在认知,因此开发者设计了位置嵌入机制:
- 相邻词元应获得更高的注意力权重
- 序列中的绝对位置不应影响相对关系
- 相对位置编码比绝对编码更有实践价值
技术演进历程
原始Transformer的位置编码采用固定公式计算后与语义嵌入相加,这种混合方式容易导致模型记忆而非泛化位置信息。随后发展的方法聚焦于改良注意力机制,让邻近词元自动获得更高权重,其中RoPE方案脱颖而出。
旋转变换的本质
RoPE通过对查询向量Q和键向量K施加旋转变换实现目标:
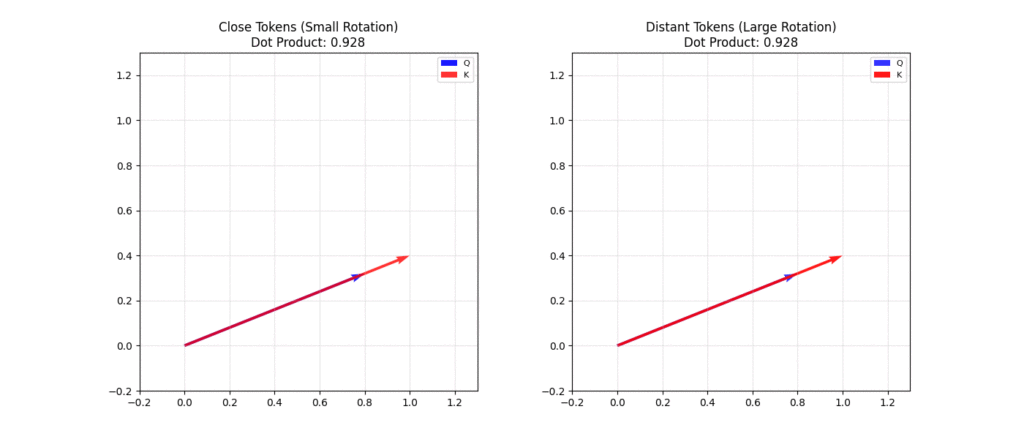
- 旋转操作保持向量模长不变,保护语义信息
- 相邻词元的旋转角度差异较小,远距离词元差异显著增大
- 在超万维空间中,反向接近的概率极低
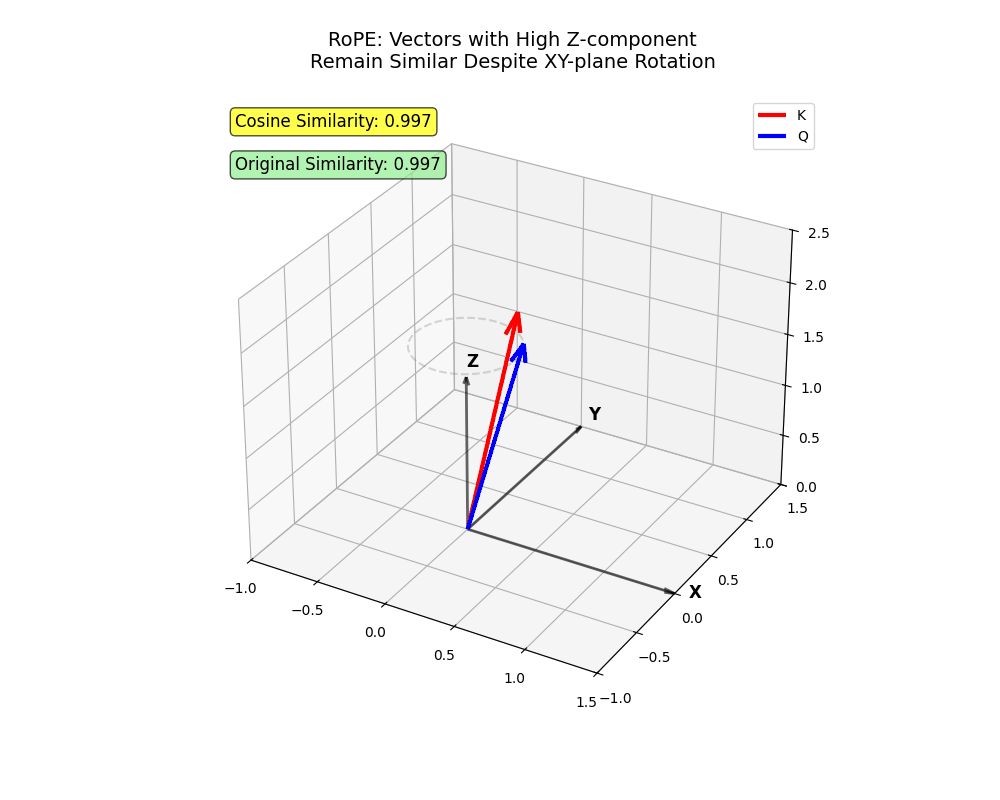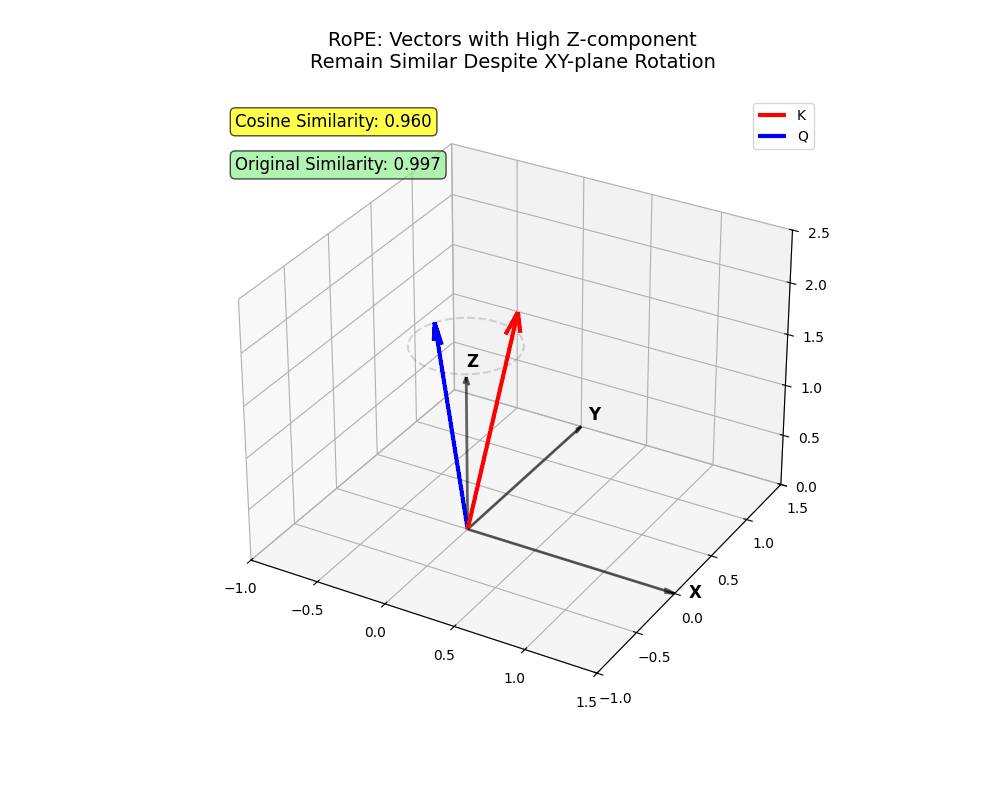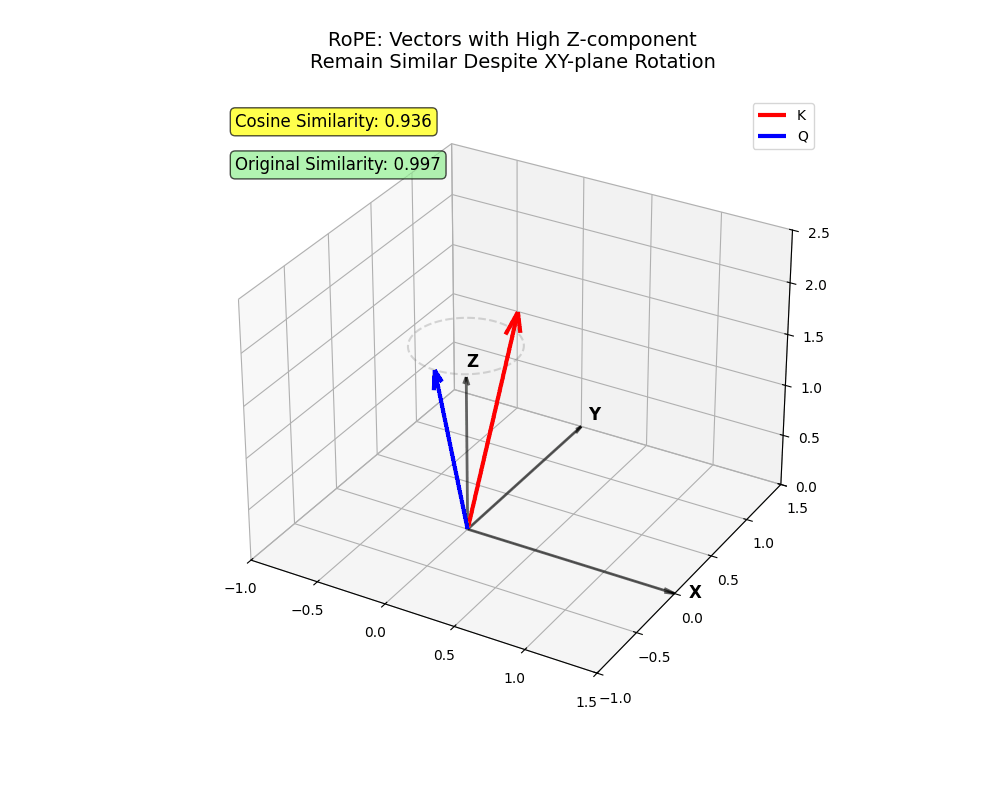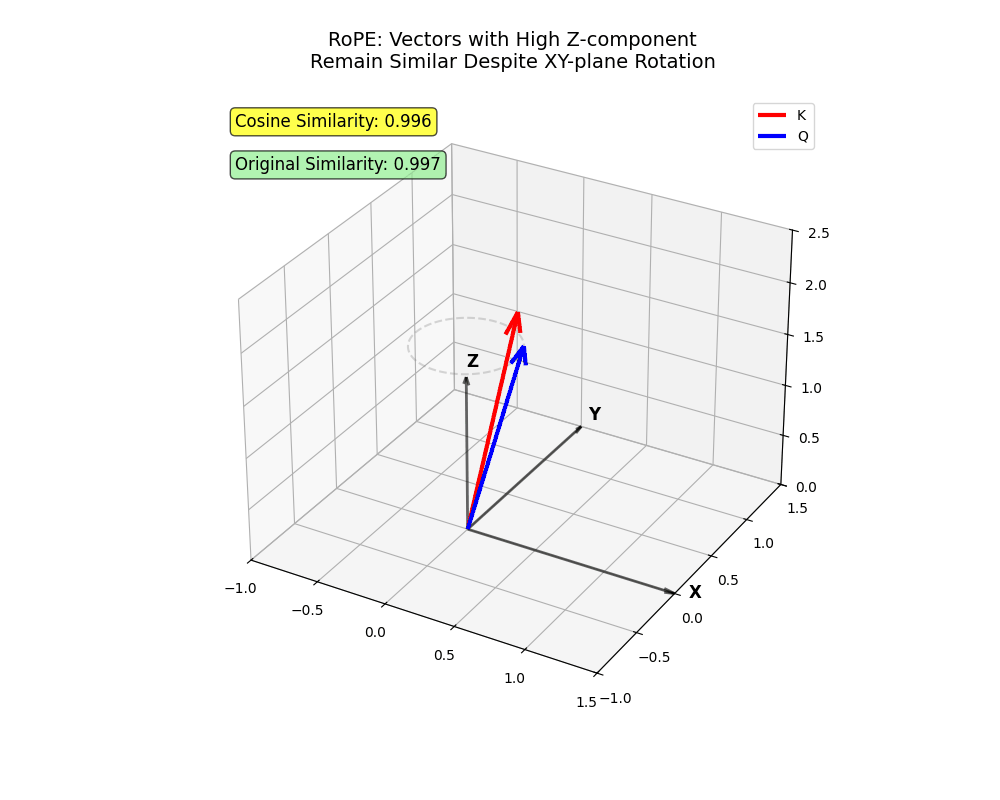
角度计算机制
旋转角度由双重因素决定:
- 绝对位置m:词元在序列中的位置
- 隐层索引i:不同维度组合对应不同旋转频率
数学表达式为:
θ = 10,000^(-2(i-1)/d)
其中d为隐层维度,10,000为预设基数。此设计使得:
- 低维度索引(i→1)对应高频率旋转
- 高维度索引(i→d/2)对应低频率旋转
工程实践优势
- 闭式公式允许无限扩展上下文长度
- 注意力权重随距离增加自然衰减
- 模型自主决定不同维度表征的距离范围
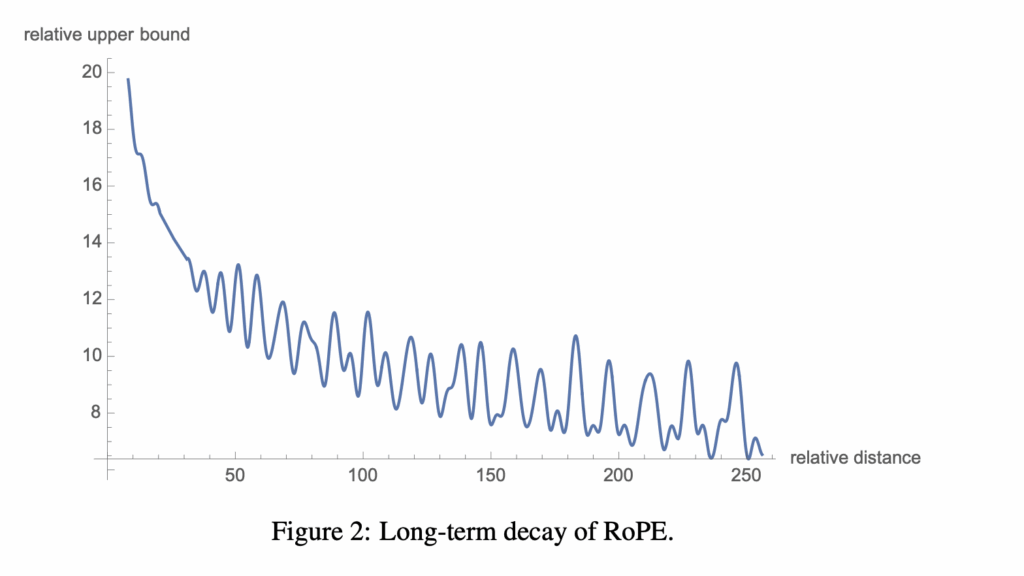
技术局限与平衡
尽管存在理论上的周期特性,实际高维空间中:
- 慢速旋转维度持续增大向量间距
- 实测显示距离与注意力相关性稳定递减
- 极端距离下可通过基数调整来优化
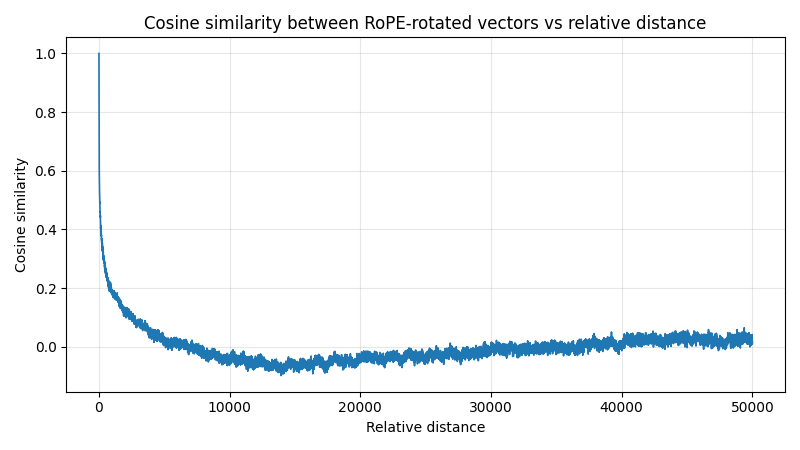
这种设计完美匹配语言特性:
- 变量定义需要长程依赖
- 形容词-名词修饰依赖短程关联







