此前文章曾深入探讨了分类模型评估中的重要指标,例如ROC-AUC(受试者工作特征曲线下面积)和科尔莫哥洛夫-斯米尔诺夫(KS)统计量。
本文将聚焦于另一个同样至关重要的分类模型评估指标——基尼系数(Gini Coefficient)。
为何需要多种分类评估指标?
每个分类评估指标都能从不同维度揭示模型的性能。众所周知,ROC-AUC主要衡量模型整体的排序能力,而KS统计量则侧重于识别正负两组之间最大差异的发生位置。
而基尼系数则独特地量化了模型在将正例(如违约客户)排位高于负例(如非违约客户)方面,相对于随机猜测的优越程度。
首先,将详细介绍基尼系数的计算方法。
为此,本文将再次以著名的德国信用数据集为例进行阐释。
沿用此前在讲解科尔莫哥洛夫-斯米尔诺夫(KS)统计量计算时所使用的样本数据,以便于对比理解。

该样本数据是通过对德国信用数据集应用逻辑回归模型后获取的。
鉴于模型输出的是概率值,从中抽取了10个样本点,以清晰演示基尼系数的计算过程。
计算方法
步骤一:根据预测概率对数据进行排序。
此处的样本数据已按预测概率降序排列。
步骤二:计算累计人口和累计正例。
累计人口:指截至当前行所累计考虑的记录数量。
累计人口百分比:指截至当前已覆盖的总人口百分比。
累计正例:指截至当前已观察到的实际正例(类别2)的数量。
累计正例百分比:指截至当前已捕获的正例百分比。

图片由作者提供
步骤三:绘制X和Y值
X轴 = 累计人口百分比
Y轴 = 累计正例百分比
此处将使用Python绘制这些X和Y值。
代码示例:
import matplotlib.pyplot as plt
X = [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
Y = [0.0, 0.25, 0.50, 0.75, 0.75, 1.00, 1.00, 1.00, 1.00, 1.00, 1.00]
# Plot curve
plt.figure(figsize=(6,6))
plt.plot(X, Y, marker='o', color="cornflowerblue", label="Model Lorenz Curve")
plt.plot([0,1], [0,1], linestyle="--", color="gray", label="Random Model (Diagonal)")
plt.title("Lorenz Curve from Sample Data", fontsize=14)
plt.xlabel("Cumulative Population % (X)", fontsize=12)
plt.ylabel("Cumulative Positives % (Y)", fontsize=12)
plt.legend()
plt.grid(True)
plt.show()
图表:
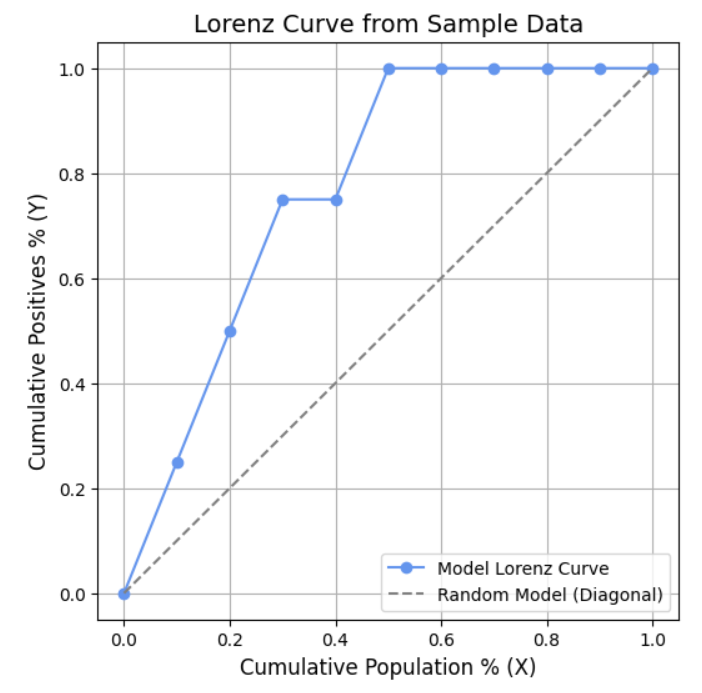
图片由作者提供
通过绘制累计人口百分比和累计正例百分比所得到的曲线,被称为洛伦兹曲线。
步骤四:计算洛伦兹曲线下的面积。
在探讨ROC-AUC时,曾提到使用梯形公式计算曲线下面积。
同样地,这里也将每两个数据点之间的区域视为一个梯形,分别计算其面积,然后将所有梯形面积累加,从而得到最终的曲线下面积。
计算洛伦兹曲线下的面积也沿用了这一方法。
洛伦兹曲线下面积计算
梯形面积公式:
ext{Area} = rac{1}{2} imes (y1 + y2) imes (x2 – x1)
从 (0.0, 0.0) 到 (0.1, 0.25):
A_1 = rac{1}{2}(0+0.25)(0.1-0.0) = 0.0125
从 (0.1, 0.25) 到 (0.2, 0.50):
A_2 = rac{1}{2}(0.25+0.50)(0.2-0.1) = 0.0375
从 (0.2, 0.50) 到 (0.3, 0.75):
A_3 = rac{1}{2}(0.50+0.75)(0.3-0.2) = 0.0625
从 (0.3, 0.75) 到 (0.4, 0.75):
A_4 = rac{1}{2}(0.75+0.75)(0.4-0.3) = 0.075
从 (0.4, 0.75) 到 (0.5, 1.00):
A_5 = rac{1}{2}(0.75+1.00)(0.5-0.4) = 0.0875
从 (0.5, 1.00) 到 (0.6, 1.00):
A_6 = rac{1}{2}(1.00+1.00)(0.6-0.5) = 0.100
从 (0.6, 1.00) 到 (0.7, 1.00):
A_7 = rac{1}{2}(1.00+1.00)(0.7-0.6) = 0.100
从 (0.7, 1.00) 到 (0.8, 1.00):
A_8 = rac{1}{2}(1.00+1.00)(0.8-0.7) = 0.100
从 (0.8, 1.00) 到 (0.9, 1.00):
A_9 = rac{1}{2}(1.00+1.00)(0.9-0.8) = 0.100
从 (0.9, 1.00) 到 (1.0, 1.00):
A_{10} = rac{1}{2}(1.00+1.00)(1.0-0.9) = 0.100
洛伦兹曲线下总面积:
A = 0.0125+0.0375+0.0625+0.075+0.0875+0.100+0.100+0.100+0.100+0.100 = 0.775
通过上述计算,得到洛伦兹曲线下的面积为0.775。
此处绘制了累计人口百分比和累计正例百分比,可以观察到该曲线下的面积直观地展示了在按预测概率排序的列表中,正例(类别2)被捕获的速度。
在样本数据集中,包含4个正例(类别2)和6个负例(类别1)。
对于一个理想的完美模型而言,当覆盖40%的人口时,便能捕获100%的正例。
完美模型的洛伦兹曲线如下图所示。
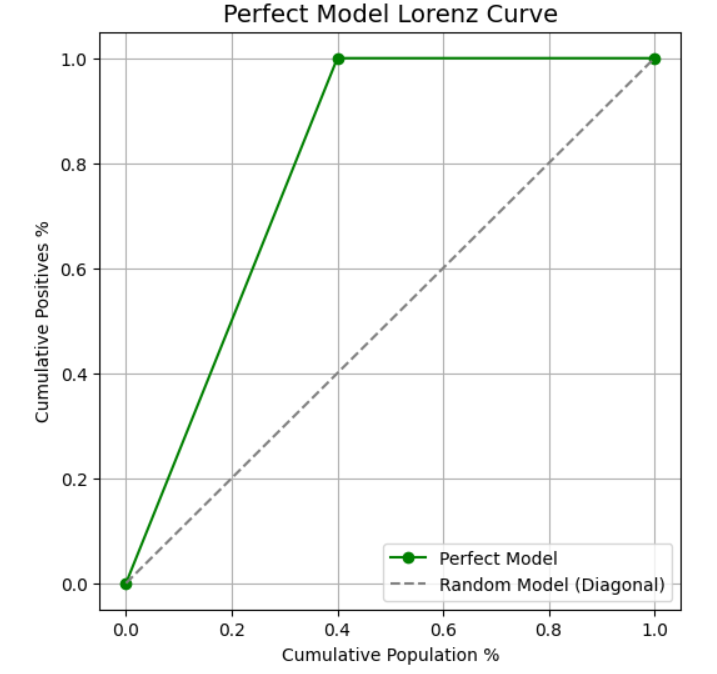
图片由作者提供
完美模型洛伦兹曲线下的面积计算。
egin{aligned} ext{Perfect Area} &= ext{Triangle (0,0 to 0.4,1)} + ext{Rectangle (0.4,1 to 1,1)} [6pt] &= rac{1}{2} imes 0.4 imes 1 ;+; 0.6 imes 1 [6pt] &= 0.2 + 0.6 [6pt] &= 0.8 end{aligned}
计算完美模型曲线下面积还有另一种方法。
ext{设 }pi ext{ 为数据集中正例的比例。}
ext{Perfect Area} = rac{1}{2}pi cdot 1 + (1-pi)cdot 1 = rac{pi}{2} + (1-pi) = 1 – rac{pi}{2}
对于此数据集:
此数据集中,10条记录中有4个正例,因此:π = 4/10 = 0.4。
ext{Perfect Area} = 1 – rac{0.4}{2} = 1 – 0.2 = 0.8
至此,已计算出样本数据集的洛伦兹曲线下面积,以及拥有相同正负例数量的完美模型的曲线下面积。
若不对数据集进行排序,正例将均匀分布。这意味着捕获正例的速率与遍历人口的速率是相同的。
这代表了随机模型,其曲线下面积始终为0.5。
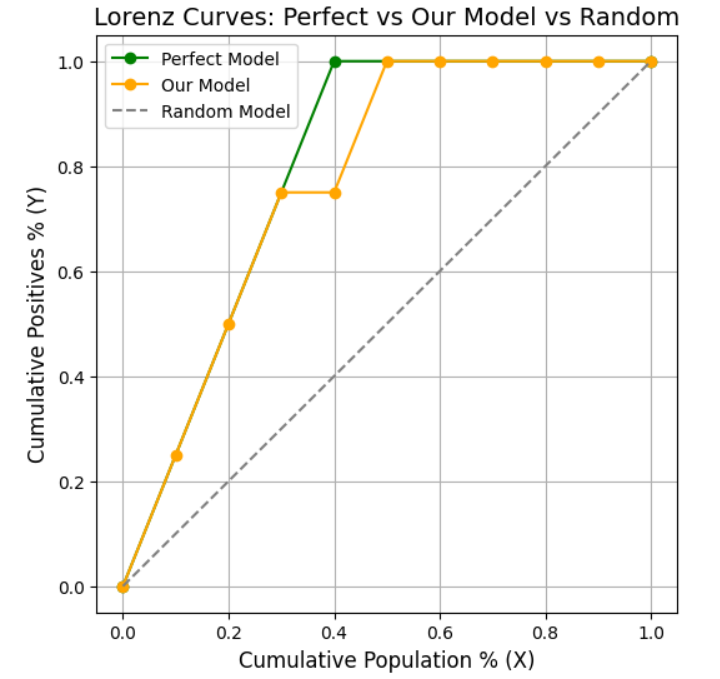
图片由作者提供
步骤五:计算基尼系数。
A_{ ext{model}} = 0.775
A{ ext{random}} = 0.5 A{ ext{perfect}} = 0.8 ext{Gini} = rac{A{ ext{model}} – A{ ext{random}}}{A{ ext{perfect}} – A{ ext{random}}} = rac{0.775 – 0.5}{0.8 – 0.5} = rac{0.275}{0.3} approx 0.92
计算结果Gini = 0.92,这表明几乎所有正例都集中在排序列表的顶部。这充分展示了模型在区分正例和负例方面的出色能力,其表现已接近完美。
在了解了基尼系数的计算方法后,进一步审视计算过程中的关键步骤。
文中选取了逻辑回归模型输出概率值的10个样本点。
随后将这些概率值按降序排列。
接着,计算了累计人口百分比和累计正例百分比,并将其绘制成图。
由此得到一条曲线,即洛伦兹曲线,其曲线下面积计算结果为0.775。
那么,0.775代表什么呢?
样本数据包含4个正例(类别2)和6个负例(类别1)。
模型输出的概率值针对类别2,这意味着概率越高,客户属于类别2的可能性越大。
在样本数据中,正例在50%的人口范围内被捕获,这表示所有正例均排名靠前。
如果模型表现完美,那么正例将在前4行(即人口的40%范围内)被完全捕获,此时完美模型的曲线下面积为0.8。
但此处的曲线下面积(AUC)为0.775,这已非常接近完美。
在此,旨在衡量模型的效率。若正例更多地集中在排序列表的顶部,则表明模型在区分正负类别方面表现出色。
随后,计算出基尼系数为0.92。
ext{Gini} = rac{A{ ext{model}} – A{ ext{random}}}{A{ ext{perfect}} – A{ ext{random}}}
分子项反映了模型相对于随机猜测的优越程度。
分母项则代表了相对于随机模型的最大可能改进空间。
这个比值综合了以上两点,使得基尼系数的取值范围始终在0(完全随机)到1(完美模型)之间。
基尼系数用于衡量模型在区分正负类别方面与完美模型的接近程度。
然而,读者可能会疑惑,为何要计算基尼系数,而不是停留在0.775这个曲线下面积的数值?
0.775是当前模型洛伦兹曲线下的面积。若不将其与完美模型(曲线下面积为0.8)进行比较,此数值本身并不能直接揭示模型与完美表现的接近程度。
因此,通过计算基尼系数将其标准化至0到1之间,从而便于不同模型之间的横向比较。
银行业界也广泛采用基尼系数,与ROC-AUC和KS统计量一同,用于评估信用风险模型。这些指标共同构成了对模型性能的全面洞察。
接下来,将计算样本数据的ROC-AUC值。
import pandas as pd
from sklearn.metrics import roc_auc_score
# Sample data
data = {
"Actual": [2, 2, 2, 1, 2, 1, 1, 1, 1, 1],
"Pred_Prob_Class2": [0.92, 0.63, 0.51, 0.39, 0.29, 0.20, 0.13, 0.10, 0.05, 0.01]
}
df = pd.DataFrame(data)
# Convert Actual: class 2 -> 1 (positive), class 1 -> 0 (negative)
y_true = (df["Actual"] == 2).astype(int)
y_score = df["Pred_Prob_Class2"]
# Calculate ROC-AUC
roc_auc = roc_auc_score(y_true, y_score)
roc_auc
计算得出AUC = 0.9583。
根据基尼系数与ROC-AUC的关系:Gini = (2 * AUC) – 1 = (2 * 0.9583) – 1 = 0.92。
这便是基尼系数与ROC-AUC之间的内在联系。
现在,将基尼系数应用于完整数据集进行计算。
代码示例:
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score
# Load dataset
file_path = "C:/german.data"
data = pd.read_csv(file_path, sep=" ", header=None)
# Rename columns
columns = [f"col_{i}" for i in range(1, 21)] + ["target"]
data.columns = columns
# Features and target
X = pd.get_dummies(data.drop(columns=["target"]), drop_first=True)
y = data["target"]
# Convert target: make it binary (1 = good, 0 = bad)
y = (y == 2).astype(int)
# Train-test split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42, stratify=y
)
# Train logistic regression
model = LogisticRegression(max_iter=10000)
model.fit(X_train, y_train)
# Predicted probabilities
y_pred_proba = model.predict_proba(X_test)[:, 1]
# Calculate ROC-AUC
auc = roc_auc_score(y_test, y_pred_proba)
# Calculate Gini
gini = 2 * auc - 1
auc, gini
计算得到基尼系数为0.60。
结果解读:
Gini > 0.5:可接受的模型性能。
Gini = 0.6–0.7:表现良好的模型。
Gini = 0.8+:卓越的模型性能,但在实际中较难达到。
数据集信息
本文所使用的数据集是德国信用数据集,该数据集可在UCI机器学习库中公开获取。其遵循知识共享署名 4.0 国际许可协议 (CC BY 4.0),这意味着在适当署名的前提下,可以自由使用和分享。






