近年来，关于量子计算的会议、研讨会、文章和书籍数量激增，这为信息处理开辟了新途径，并促使人们重新思考经典系统的局限性。经典与量子研究之间的相互作用也推动了混合算法的发展，这些算法将熟悉的经典技术与量子资源相结合。本文将介绍量子计算的基本原理，并探讨其在数据科学领域的进一步应用。
随着2025年诺贝尔物理学奖 [1] 表彰量子隧道效应的进展，量子技术在未来几年将变得更加普及。这项自20世纪80年代发展起来的关键思想在于，量子隧道效应使得设备能够将叠加态、纠缠和干涉（定义参见图1）转化为可工程化的工具。这意味着研究人员可以在真实的量子芯片上运行实际的算法，而不仅仅停留在模拟层面，从而探索更高效地从高维数据中学习的新方法。
在深入探讨基础知识之前，有必要思考为何量子技术对当前工作流程至关重要。核心问题是：
当今方法存在哪些局限，迫使研究人员需要重新审视其方法，并考虑超越现有工具的替代方案？
摩尔定律的局限性：
1965年提出的摩尔定律预测，芯片上的晶体管数量（以及计算能力）大约每两年翻一番。这一预期通过持续的晶体管微型化推动了几十年的技术进步：芯片每两年能够容纳大约两倍的晶体管，从而使计算变得更便宜、更快速 [2]。
然而，随着工程师将晶体管尺寸推向原子尺度，他们面临着严峻的物理限制：在相同面积内集成更多更小的设备，会迅速增加散热和功耗密度，使冷却和稳定性管理变得异常困难。在微小尺度下，电子会泄漏或偏离其预期路径，导致功耗损失并使芯片行为变得不可预测，这可能导致错误或性能下降。此外，导线、内存和输入/输出系统无法像晶体管那样高效扩展，从而对整体系统性能造成严重的瓶颈 [2]。
所有这些障碍都清楚地表明，摩尔定律预测的指数级增长无法无限期地持续下去；仅仅依靠尺寸缩小已不再可行。相反，当前的进步取决于更优的算法、专业的硬件，以及在适当情况下，利用量子方法解决选定高影响力子问题的最优算法。
随着数据量持续增长和计算需求不断升级，深度学习及其他现代人工智能方法在时间、能源和内存效率方面正达到实际极限。量子计算提供了一条不同的路径，它通过叠加态、纠缠和干涉来处理信息，允许某些计算更高效地进行。量子机器学习（QML）的目标是使用量子比特（qubits）而不是经典比特来表示和转换数据，这可能比经典系统更有效地处理高维或不确定性问题。尽管目前的硬件仍在发展中，但QML的概念基础已经指向了一个量子和经典资源协同工作以克服计算瓶颈的未来。
安全范式
传统的加密方法依赖于经典计算机难以解决的复杂数学问题。然而，量子计算机可能通过利用像肖尔算法（量子计算优势的例子之一）[3] 这样的量子算法，迅速破解许多现有系统。许多基于量子的安全创新正日益从理论走向实践，应用于对数据保护标准要求最高的行业。
这种风险的一个具体例子被称为“先收割后解密”：攻击者现在捕获并存储加密数据，即使他们暂时无法解密。一旦大规模量子计算机问世，他们就可以利用量子算法追溯性地解密这些信息，从而暴露敏感数据，例如健康记录、金融交易或机密通信 [4]。
为应对这一挑战，Google Chrome浏览器已将量子抗性（Quantum-Resistance）纳入其功能。自版本116起，Chrome实施了一种混合密钥协商算法（X25519Kyber768），该算法将传统的椭圆曲线密码学与Kyber相结合，后者是NIST（美国国家标准与技术研究院）为抗量子加密标准化算法之一 [5]。这种方法能够同时保护数据免受经典攻击和未来的量子攻击。
数学复杂性
利用量子原理可以比传统方法更有效地探索广阔的解决方案空间。这使得量子方法在优化、机器学习和仿真等具有高计算复杂度（大O表示法，即工作量随问题规模的增长速度）的问题中前景广阔。例如，大整数分解在计算上之所以困难，主要源于其数学复杂性，而非内存或暴力破解的限制。这意味着对于像加密系统中使用的大数而言，在经典计算机上分解大数实际上是不可能完成的任务。
理解基本原理
为了更深入地理解这些主题，有必要掌握量子力学的基本规则以及它们与当前使用的经典观点的区别。
在经典计算中，数据被表示为比特，其值可以是0或1。这些比特通过逻辑运算或逻辑门（AND、OR、NOT、XOR、XNOR）进行组合和操作，以执行计算并解决问题。然而，经典计算机能够存储和处理的信息量受到其比特数量的限制，只能表示有限数量的0和1的可能组合。因此，某些计算，例如分解大数，对于传统计算机而言非常困难。
另一方面，在量子计算中，数据被表示为量子比特，或称qubits，由于叠加态、干涉和纠缠的原理，它们可以同时具有0和1的值。这些原理允许量子系统并行处理信息，并更快地解决某些问题。这被称为“量子猫态”或薛定谔的猫态。
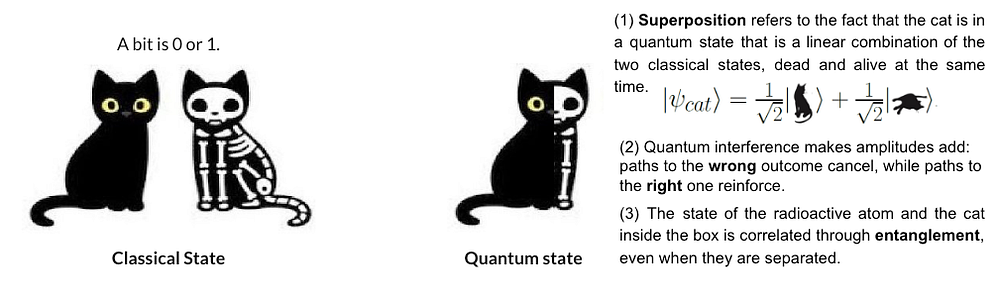
图1：使用薛定谔的猫类比，说明经典态与量子态之间的区别。在经典态（左侧）中，猫要么活着要么死了，对应于比特为0或1。在量子态（右侧）中，猫同时处于两种状态的叠加态。量子干涉和纠缠进一步定义了这些状态如何相互作用并保持关联。图片由作者提供。
这个概念可以通过薛定谔的猫实验（图1）来解释，其中在一个封闭机制中使用了一个假设的放射性原子，如果被触发，可能会结束一只被困在里面的猫的生命 
。其思想是，原子处于激活或不激活机制的叠加态中，同时与猫的状态纠缠在一起，因此，在原子状态明确之前，猫的状态仍然处于既活着 
又死了 
的叠加态。薛定谔实验中的猫的状态并非物质的真实状态，而是一个用来解释量子系统奇异行为的理论概念。
一个类似的例子可以用量子硬币（一个更恰当且保护猫咪 
的例子）来阐述 [6]。一枚普通硬币总是只有一面朝上，要么是正面，要么是反面，但一枚量子硬币可以同时处于两种可能性的叠加态，直到被观察为止。当有人检查时，叠加态会坍缩成一个确定的结果。硬币还可以与其测量设备或系统纠缠在一起，这意味着知道其中一个的状态会立即确定另一个的状态（无论初始经典条件如何）。干涉进一步修改了概率：有时波会叠加，使某种结果更可能发生，而在其他情况下则相互抵消，使其可能性降低。即使是启动、抛掷和落地等动作，也可能涉及量子相位并产生叠加态或纠缠。
基于这些思想，一个n量子比特寄存器存在于一个具有2^n种可能状态的空间中，这意味着它可以表示复杂的量子振幅模式。然而，这并不意味着n个量子比特存储了2^n个经典比特，也并非所有答案可以一次性读取。当系统被测量时，状态会坍缩，并且每次运行只能获得有限的经典信息，大约n个比特。量子计算的强大之处在于设计算法，通过巧妙地准备和操纵叠加态和相位，使得干涉作用增强正确结果的可能性，同时抑制错误结果的可能性。叠加态和纠缠是核心资源，但真正的量子优势取决于这些效应如何在特定算法或问题中得到利用。
不同的方法
量子计算有多种不同的方法，它们在使用量子比特、控制方式、所需条件以及擅长解决的问题上有所不同。图2总结了主要选项，随着该领域的成熟，更先进的技术将持续涌现。
图2. 量子计算不同方法概览。每种方法在目的、可扩展性及量子优势程度方面各异。图片由作者提供。
在门模型量子计算机和量子退火器中，随着量子系统规模的扩大（例如拥有大量量子比特或像大数分解这样复杂的问题），经典计算机上的模拟变得不切实际，因为其对资源的需求呈指数级增长。需要真实的量子硬件才能在大规模上观察到真正的量子加速。然而，经典计算机在今天仍然扮演着至关重要的角色，它允许研究人员和从业者模拟小型量子电路，并尝试使用模拟量子行为但不需要量子硬件的量子启发算法。
当需要使用真正的量子设备时，主要通过云平台（如IBM Quantum、Rigetti、Azure Quantum、D-Wave）进行访问。Qiskit或PennyLane等库允许研究人员在经典模拟器上进行原型开发，并通过凭证将任务提交到真实硬件。模拟对于开发至关重要，但无法完美捕捉物理限制（噪声、连接性、排队、设备尺寸）。
门模型：
在门模型硬件上，第一步通常是设置一个电路，用于编码解决问题所需的量子态。因此，已知信息被编码成量子比特或qubits的量子态，并通过量子门进行控制。这些量子门类似于经典计算中的逻辑运算，但它们作用于量子比特，并利用叠加态、纠缠和干涉等量子特性。将量子态编码到电路中有很多种方法，并且根据编码方式的不同，错误率可能会有很大差异。这就是为什么使用纠错技术来修正错误并使计算更准确的原因。所有操作和计算完成后，结果需要被解码，以便在正常的经典世界中理解它们。
在QML或量子机器学习领域，核方法和变分算法被用于编码和构建模型。这些技术的方法与经典机器学习中使用的有所不同。
- 变分算法（VQAs）：定义一个参数化电路，并使用经典优化方法根据损失函数调整参数（例如，用于分类）。示例包括量子神经网络（QNNs）、变分量子本征求解器（VQE）和量子近似优化算法（QAOA）。
- 量子核方法：构建量子特征映射并测量相似性，以供经典分类器或聚类器使用。示例包括量子支持向量机（QSVM）、量子核估计（QKE）和量子k均值。
QML算法，如基于核方法和变分算法，在优化和图像识别等领域已显示出有前景的结果，并有可能彻底改变医疗保健、金融和网络安全等各个行业。然而，许多挑战依然存在，例如对稳健纠错技术的需求、量子硬件的高成本以及量子专家短缺的问题。
量子退火
许多现实世界中的问题都是组合型的，其可能性呈阶乘级增长（例如10!、20!等），使得穷举搜索变得不切实际。这些问题通常可以自然地映射到图结构上，并可表述为二次无约束二元优化（QUBO）或伊辛（Ising）模型。量子退火器加载这些问题表述，并搜索低能量（最优或接近最优）状态，为具有图结构的优化任务提供了一种替代的启发式方法。在与强经典基线在相同时间约束下进行公平比较时，量子退火可以显示出具有竞争力的性能。
在QML中，量子退火可应用于优化机器学习模型中的参数、发现模式或通过寻找代表解决方案的最小能量配置来进行聚类。尽管量子退火器是硬件特定且专业化的，但它们在机器学习和优化方面的实际应用使其成为门模型QML的重要补充方法。
量子退火器通常作为启发式求解器，并在相似时间约束下与经典强基线进行比较。它们通常通过云服务（如D-Wave）进行访问，其噪声和硬件限制使其与门模型量子计算机有所区别。
量子启发
这些是经典算法，它们模仿了量子计算的思想（例如，退火式搜索、张量方法）。它们在CPU/GPU上运行（无需量子硬件），并作为强大的基线。研究人员可以使用标准的Python栈或专门的软件包来大规模尝试它们。
量子启发算法通过在经典计算中利用量子原理，提供了一个实用的桥梁，为某些问题类别提供了潜在的加速，而无需昂贵的量子硬件。然而，它们并未提供真正的量子计算的全部优势，其性能提升在很大程度上取决于问题和实现细节。
案例分析：
当今的量子优势仍处于萌芽阶段，并且高度依赖于具体问题。最大的收益预计将出现在那些量子算法可以利用其结构的高复杂度问题上。本节提出的玩具示例仅作说明之用，旨在突出不同方法之间的差异，但真正的优势更可能出现在目前经典计算机难以解决或无法处理的问题上。
在这个例子中，研究人员使用了一个表格化的模拟数据集，其中大部分点是正常的，一小部分是异常的（图3）。在这个演示中，正常对应于原点周围的密集簇，而异常则形成几个远离原点的小簇。
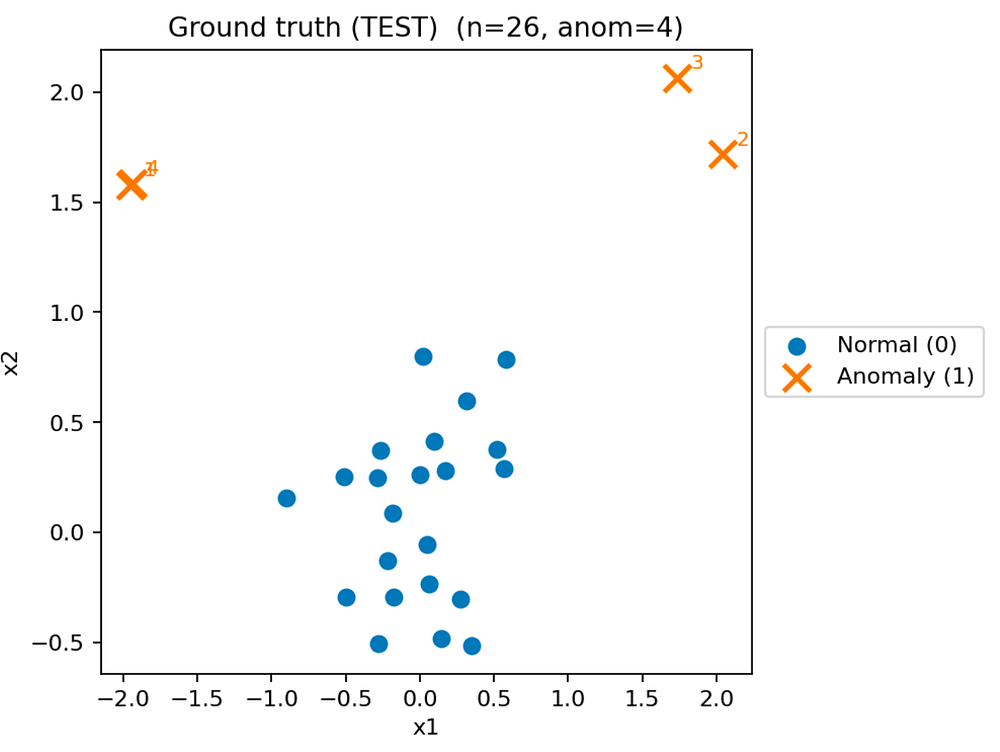
图3.正常点和异常点的真实分布（测试集）。图片由作者提供。
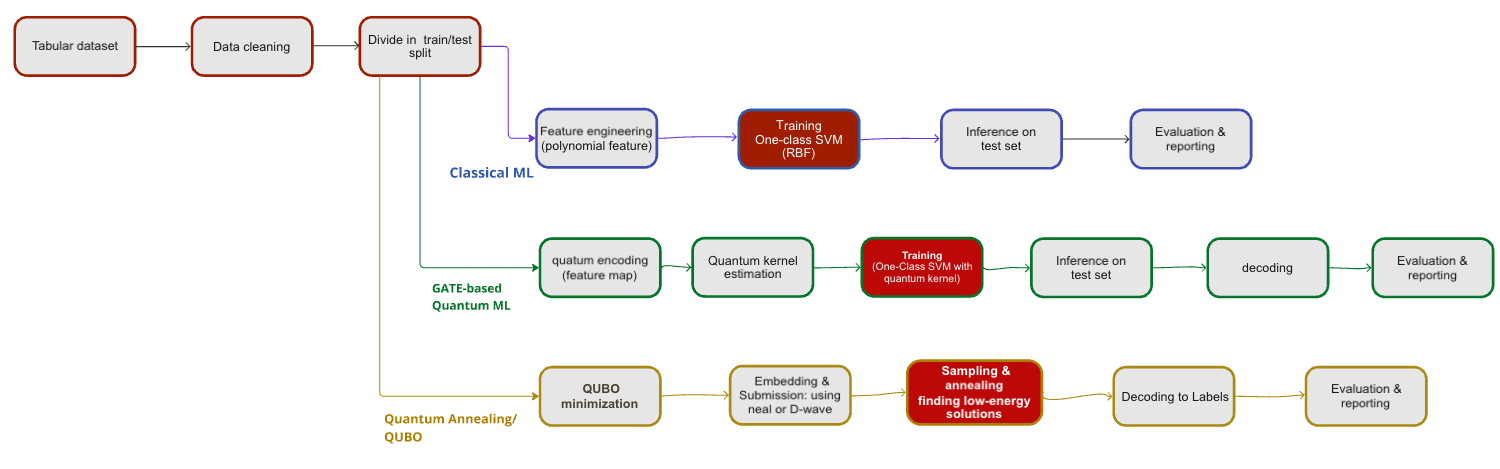
图4.用于异常检测的三种建模方法概览。
从相同的表格数据集出发，工作流程分为三条路径：（1）经典机器学习（基线），（2）基于门模型的量子机器学习和（3）量子退火（QUBO）。图片由作者提供。
图4的图表展示了一个统一的工作流程，利用三种不同的方法在相同表格数据集上进行异常检测：（1）经典机器学习（单类支持向量机）[7]，（2）基于门模型的量子机器学习（量子核方法）[8]，以及（3）量子退火启发式优化。首先，数据集经过清洗、缩放，并划分为训练集、验证集和测试集。对于经典路径，应用多项式特征工程后训练单类支持向量机并评估预测结果。基于门模型的量子机器学习选项使用量子映射编码特征，并估计量子核以进行训练和推理，然后解码并评估。退火路径将任务表述为QUBO问题，通过模拟退火求解，解码结果并评估性能。每种方法都产生其自身的异常预测输出和评估指标，提供了对数据的补充视角，并展示了经典和量子启发工具如何集成到在经典计算机上运行的单一分析管道中。
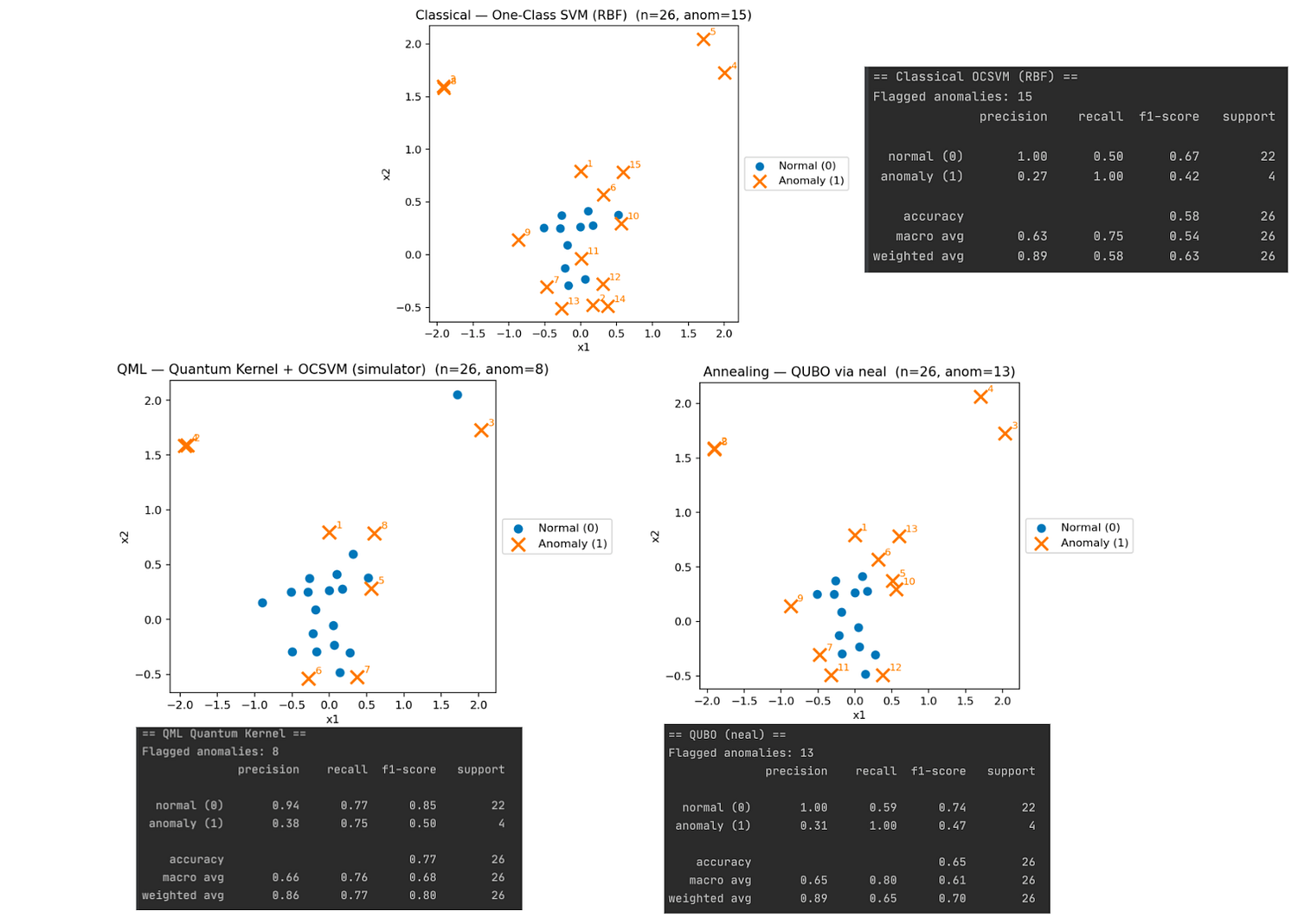
图5. 三种异常检测方法的比较。
在测试数据集上使用(A) 经典单类支持向量机、(B) 量子核OCSVM（使用PennyLane进行门模型QML模拟）和(C) 基于QUBO的模拟退火方法（量子启发）的可视化结果。每个图中显示正常点（蓝色）和预测异常点（橙色）。图片由作者提供。
在这个微小、不平衡的测试集（22个正常点，4个异常点）上，这三种方法的表现各不相同。量子核OCSVM取得了最佳平衡：通过捕获大部分异常（召回率0.75）实现了更高的整体准确率（约0.77），同时将误报率控制在低于其他方法。经典OCSVM（RBF核）和退火式QUBO都达到了1.0的召回率（它们都找到了全部4个异常），但过度标记了正常点，因此它们的准确率有所下降（分别为≈0.58和0.65）。
此处的目的是演示而非性能：这个例子展示了如何使用这些方法，结果并非关注的重点。它还说明了特征映射或表示可能比分类器本身更重要。
任何关于量子优势的声称最终都取决于规模：问题大小和结构、电路深度和宽度、特征映射中的纠缠，以及在真实量子硬件上运行以利用干涉而非仅仅模拟干涉的能力。在此并未声称量子优势；这是一个经典计算机能够解决的简单问题，即使是使用量子启发思想。
何时转向量子计算
从模拟器开始是明智之举，只有当有明确的效益信号时才转向真实量子硬件。模拟器快速、经济且可重现：研究人员可以在相同的时间/成本预算下，与强大的经典基线一同原型开发量子风格的方法（例如量子核、QUBO）。这使得研究人员能够调整特征映射、超参数和问题编码，并观察是否有任何方法在准确性、获得良好解决方案的时间、鲁棒性或扩展趋势方面表现更好。
随后，在有充分理由时才使用硬件：例如，当模拟器显示出有前景的扩展趋势时，当问题结构与设备匹配时（例如良好的QUBO嵌入或浅层门电路），或者当利益相关者需要硬件验证时。在硬件上，研究人员需要衡量在噪声和连接性限制下的质量-时间-成本，应用错误缓解技术，并与经过优化的经典方法进行公平比较。简而言之：先模拟，再转向量子以验证实际性能；只有当硬件结果和趋势线确实值得时才采纳量子方法。
如前所述，当今的量子优势仍处于萌芽阶段，并且高度依赖于具体问题。真正的挑战和机遇在于，将有前景的模拟转化为在经典计算仍难以解决的问题上获得经过硬件验证的收益，并在问题规模增长时，在质量、时间成本方面展现出明显的改进。
量子机器学习在模型压缩和可扩展性方面具有超越经典方法的潜力，尤其是在网络安全等数据密集型领域。挑战在于处理庞大的数据集，其中包含数百万个正常交互和极少数攻击。量子模型可以利用叠加态和纠缠，将复杂模式压缩成紧凑的量子表示，从而即使在不平衡数据中也能实现更高效的异常检测。混合量子-经典学习和联邦量子学习方法旨在提高可扩展性和隐私性，使实时入侵检测更具可行性。尽管当前硬件存在局限性，但研究表明量子压缩可以使未来的模型更有效地管理更大、更复杂的网络安全数据流，为强大的实用防御铺平道路。
参考文献
[1] 诺贝尔物理学奖2025。NobelPrize.org。诺贝尔奖外展（2025）。“摘要”。2025年10月19日访问。https://www.nobelprize.org/prizes/physics/2025/summary/
[2] DataCamp。（无日期）。摩尔定律：它是什么，它已经死了吗？2025年10月2日检索。https://www.datacamp.com/tutorial/moores-law
[3] Classiq。（2022年7月19日）。量子密码学 — 肖尔算法解释。Classiq Insights。https://www.classiq.io/insights/shors-algorithm-explained
[4] Gartner。（2024年3月14日）。立即开始过渡到后量子密码学。2025年10月10日检索。https://www.gartner.com/en/articles/post-quantum-cryptography
[5] The Quantum Insider。（2023年8月14日）。谷歌在Chrome浏览器中推进抗量子密码学工作。2025年10月10日检索。https://thequantuminsider.com/2023/08/14/google-advances-quantum-resistant-cryptography-efforts-in-chrome-browser/
[6] “薛定谔的猫硬币（古董银）”作者：BeakerHalfFull（2025年10月16日访问）。摘自： Etsy：https://www.etsy.com/listing/1204776736/schrodingers-cat-coin-antique-silver
[7] Scikit-learn开发者。“带有非线性核（RBF）的单类SVM。”scikit-learn文档，https://scikit-learn.org/stable/autoexamples/svm/plotoneclass.html。2025年10月21日访问。
[8] Schuld, Maria。“使用scikit-learn进行量子模型的基于核的训练。”PennyLane演示，https://pennylane.ai/qml/demos/tutorialkernelbased_training。2021年2月2日发布。2025年9月22日更新。2025年10月21日访问。
