深度强化学习从入门到实践：零基础探索无人机智能降落

您是否曾好奇，如何在不预先编程每个动作的情况下，教会机器人自主降落无人机？本文正是为了探索这一课题。研究团队投入数周时间构建了一款模拟游戏，其中一架虚拟无人机必须学会如何在平台上着陆——它不是通过遵循预设指令，而是通过不断试错来学习，就像人类学习骑自行车一样。

这就是强化学习（Reinforcement Learning, RL）的核心理念，它与其他机器学习方法有着根本性的区别。系统不再向人工智能展示数千个“正确”降落的范例，而是通过给予反馈来引导其学习：“嘿，这次表现不错，但下次或许可以更轻柔一些？”或者“糟糕，坠毁了——下次尽量避免。”通过无数次的尝试，人工智能智能体逐渐摸索出哪些策略有效，哪些无效。

本文记录了从 RL 基础到构建一个工作系统（大部分情况下能够教会无人机降落）的全过程。读者将看到其中的成功、失败以及过程中需要调试的各种异常行为。

1. 强化学习：概览

强化学习的许多理念都可以追溯到巴甫洛夫的狗和斯金纳的鼠实验。其核心思想是，当主体做出期望行为时，系统会给予“奖励”（正向强化）；当主体做出不良行为时，则会施以“惩罚”（负向强化）。通过多次重复尝试，主体从这些反馈中学习，逐渐发现哪些行动能带来成功——这类似于斯金纳的实验鼠如何学会按压哪个杠杆能获得食物奖励。

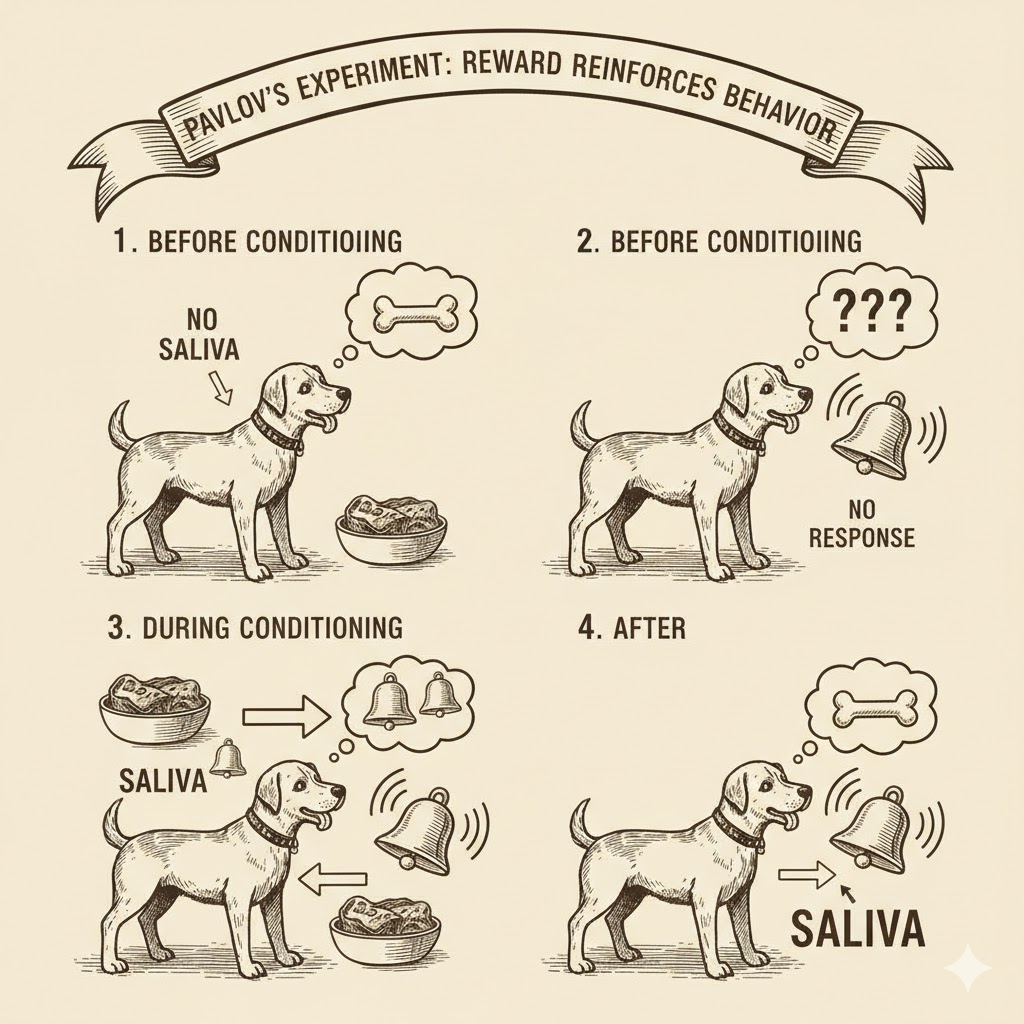
图1. 巴甫洛夫经典条件反射实验（由 Google Gemini AI 生成）

同样，人们希望构建一个能够学习执行任务的系统，使其能够最大化奖励并最小化惩罚。请注意这个最大化奖励的事实，它将在后续内容中发挥重要作用。

1.1 核心概念

在讨论可以在计算机上通过编程实现的系统时，最佳实践是为可以抽象化的概念提供清晰的定义。在人工智能（特别是强化学习）的研究中，核心思想可以归结为以下几点：

1. 智能体（Agent 或 Actor）：这是前文提到的“主体”。它可以是巴甫洛夫的狗、一架试图在大型工厂中导航的机器人、一个视频游戏中的非玩家角色（NPC）等。
2. 环境（Environment 或 The World）：这可以是一个场所、一个带有约束条件的模拟器、一个视频游戏的虚拟世界等。可以将之类比为：“一个真实的或虚拟的‘盒子’，智能体的全部‘生活’都被限制在其中；它只了解盒子内发生的事情。而作为‘掌控者’，研究人员可以改变这个盒子，智能体则会认为这是‘神明’在施加意志。”
3. 策略（Policy）：就像政府、公司和许多类似实体中的“政策”一样，“策略”规定了“在给定特定情况时应采取何种行动”。
4. 状态（State）：这是智能体“看到”或“知道”的当前情况。可以将其视为智能体在任何给定时刻对现实的快照——就像在驾驶时，看到交通灯的颜色、当前车速以及与交叉口的距离。
5. 行动（Action）：当智能体能够“感知”环境中的事物时，它可能会希望采取行动来应对当前状态。比如，它想喝咖啡，第一件事就是“下床”。这就是智能体为实现目标（即喝咖啡！）而采取的行动。
6. 奖励（Reward）：每次智能体自愿执行一个行动后，环境中可能会发生一些变化。例如，智能体起床后，因不善行走而跌倒。在这种情况下，“掌控者”（即系统设计者）会施以惩罚（负向奖励）。但当智能体成功抵达厨房并拿到咖啡时，“掌控者”则会给予奖励（正向奖励）。

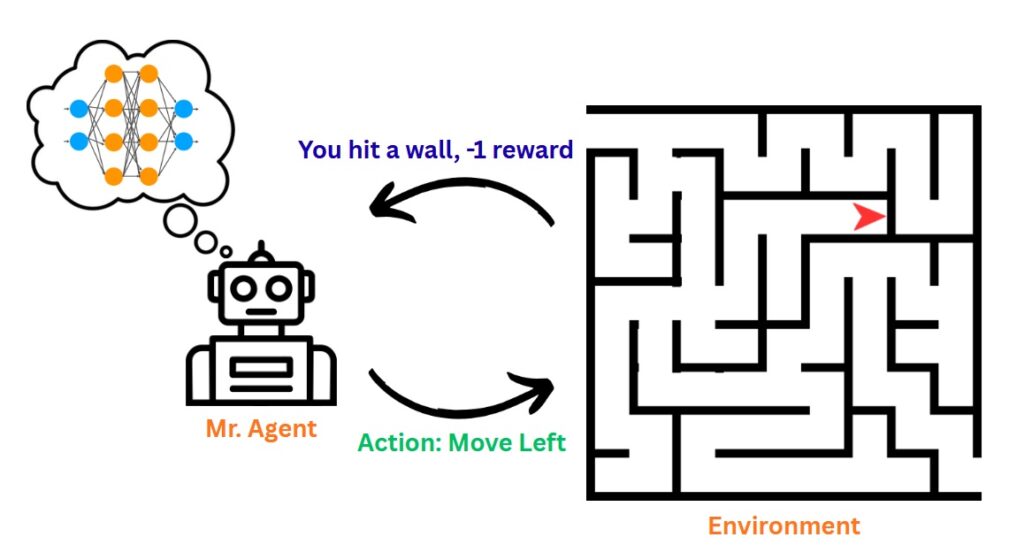
图2. 理论强化学习系统示意图

可以想象，这些关键组成部分大多需要根据智能体需要解决的特定任务/问题进行定制。

2. 模拟环境

既然了解了基础知识，读者可能会好奇：究竟如何构建这样一个系统？下面将展示研究团队构建的游戏。

为了本文，研究人员编写了一款定制视频游戏，任何人都可以访问并使用它来训练自己的机器学习智能体来玩游戏。

完整的代码库可在GitHub上找到（欢迎点赞收藏）。该代码库将用于更多游戏和仿真代码，以及在后续强化学习系列文章中将实现的更高级技术。

送货无人机

送货无人机是一款目标是将无人机（可能载有货物）降落在平台上的游戏。要赢得游戏，智能体必须成功着陆。成功着陆需要满足以下条件：

1. 处于平台降落范围内
2. 速度足够慢
3. 机身保持竖直（倒着陆更像是坠毁而非降落）

所有关于如何运行游戏的信息都可以在 GitHub 存储库中找到。

以下是游戏的界面截图：

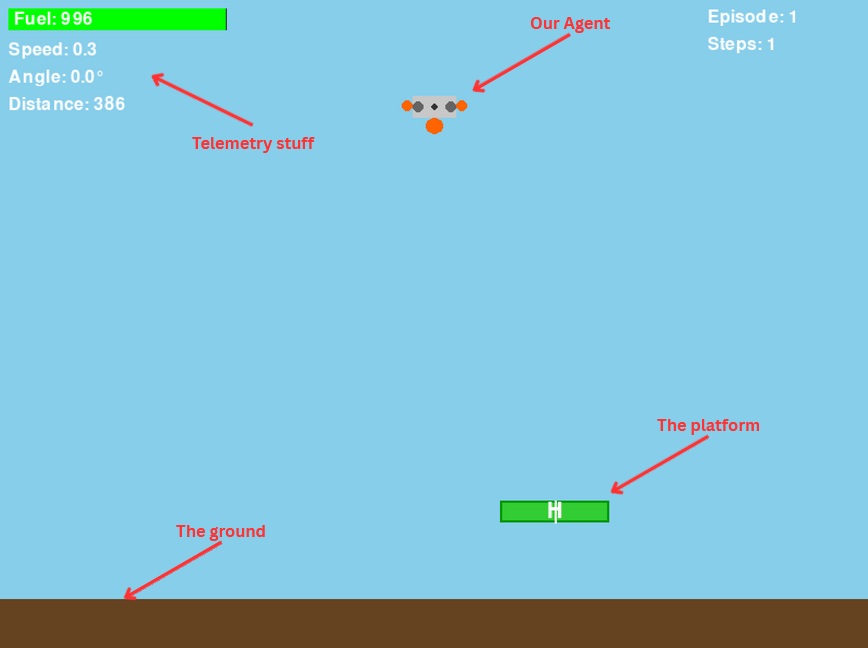
图3. 本项目制作的游戏截图

如果无人机飞出屏幕或触地，将被视为“坠毁”情况，导致任务失败。

状态描述

无人机观察 15 个连续值，这些值完整描述了其当前状况：

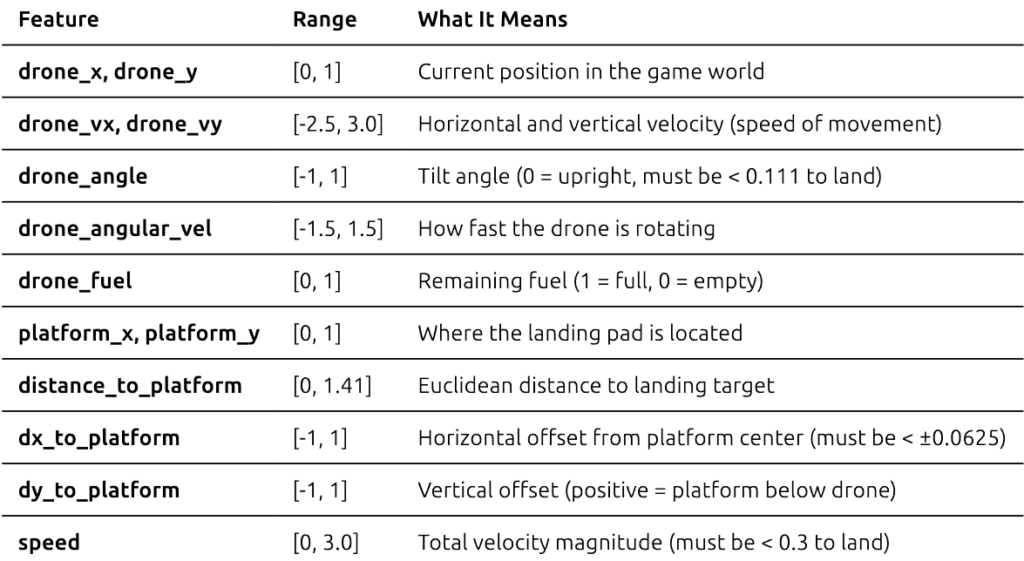
降落成功标准：无人机必须同时满足：

1. 水平对齐：在平台边界内（|dx| < 0.0625）
2. 安全接近速度：小于 0.3
3. 水平姿态：倾斜度小于 20°（|angle| < 0.111）
4. 正确高度：无人机底部接触平台顶部

这就像侧方停车一样——需要正确的位置、正确的角度和足够慢的速度才能避免撞车！

如何设计策略？

设计策略的方法有很多种。它可以是贝叶斯方法（维持信念的概率分布）、一个针对离散状态的简单查找表、一个手动编码的规则系统（“如果距离 < 10，则刹车”）、一棵决策树，或者——正如本文将探讨的——一个通过梯度下降学习状态到行动映射的神经网络。

实际上，人们需要一个能够接收上述状态、利用该状态进行一些计算并返回应执行动作的系统。

深度学习构建策略？

那么，如何设计一个能够处理连续状态（例如精确的无人机位置）并学习复杂行为的策略呢？这就是神经网络发挥作用的地方。

在神经网络（或深度学习）中，通常最好处理行动概率，即“在当前状态下，哪个行动最可能是最佳选择？”因此，可以定义一个神经网络，它将状态作为“向量”或“向量集合”作为输入。这个向量或向量集合必须由观察到的状态构建。对于送货无人机游戏，状态向量为：

状态向量（来自 2D 无人机游戏）

无人机观察其绝对位置、速度、姿态、燃料、平台位置以及派生指标。连续状态为：

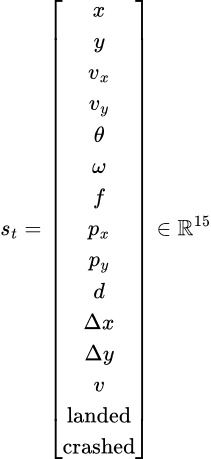
其中每个分量代表：

所有分量都被归一化到大致 [0,1] 或 [-1,1] 范围，以实现稳定的神经网络训练。

行动空间（三个独立的二元推进器）

与离散行动组合不同，本文将每个推进器独立处理：

• 主推进器（向上推力）
• 左推进器（顺时针旋转）
• 右推进器（逆时针旋转）

每个行动都从伯努利分布中采样，每个时间步提供 3 个独立的二元决策。

神经网络策略（带有伯努利采样的概率策略）

设 f θ(s) 为 Sigmoid 激活后的网络输出。该策略使用独立的伯努利分布：

最小化 Python 代码（来自实现）

# build state vector from DroneState
s = np.array([
    state.drone_x, state.drone_y,
    state.drone_vx, state.drone_vy,
    state.drone_angle, state.drone_angular_vel,
    state.drone_fuel,
    state.platform_x, state.platform_y,
    state.distance_to_platform,
    state.dx_to_platform, state.dy_to_platform,
    state.speed,
    float(state.landed), float(state.crashed)
])

# network outputs probabilities for each thruster (after sigmoid)
action_probs = policy(torch.tensor(s, dtype=torch.float32))  # shape: (3,)

# sample each thruster independently from Bernoulli
dist = Bernoulli(probs=action_probs)
action = dist.sample()  # shape: (3,), e.g., [1, 0, 1] means main+right thrusters

这展示了如何将游戏的物理观测值映射到 15 维归一化状态向量，并为每个推进器生成独立的二元决策。

代码设置（第一部分）：导入和游戏套接字设置

首先需要启动游戏套接字监听器。为此，可以导航到代码库中的 `delivery_drone` 目录，并运行以下命令：

pip install -r requirements.txt # 首次运行以设置所需模块
python socket_server.py --render human --port 5555 --num-games 1 # 在需要以套接字模式运行游戏时运行

注意：运行代码需要 PyTorch。请务必提前设置好。

import os
import torch
import torch.nn as nn
import math
import numpy as np

from torch.distributions import Bernoulli

# Import the game's socket client
from delivery_drone.game.socket_client import DroneGameClient, DroneState

# setup the client and connect to the server
client = DroneGameClient()
client.connect()

如何设计奖励函数？

那么，一个好的奖励函数应该具备什么特点？ 这可以说是强化学习中最困难的部分（也通常是调试过程中耗时最多的部分）。

奖励函数是任何强化学习实现的核心（如果设计不当，智能体可能会做出非常诡异的行为）。理论上，它应该定义哪些“好”行为应该被学习，哪些“坏”行为不应该被学习。智能体采取的每个行动都由该行动所展现的每个行为特征的总累积奖励来表征。例如，如果希望无人机平稳降落，可能会对接近平台和缓慢移动给予正向奖励，同时惩罚坠毁或燃料耗尽——智能体随后会学习如何最大化所有这些奖励随时间推移的总和。

优势：衡量有效奖励的更好方式

在训练策略时，人们不仅想知道某个行动是否带来了奖励，还想知道它是否“比平时更好”。这就是优势（advantage）背后的直觉。

优势告诉我们：“这个行动比通常预期的表现更好还是更差？”

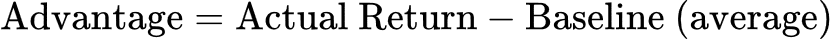
在实现中，研究团队：

1. 收集多个回合并计算其回报（总折扣奖励）。
2. 计算基线（baseline）作为所有回合的平均回报。
3. 为每个时间步计算优势 = 回报 – 基线。
4. 将优势归一化，使其均值为 0，标准差为 1（为了稳定训练）。

这为什么有帮助：

• 具有正向优势的行动 → 优于平均水平 → 增加其概率。
• 具有负向优势的行动 → 劣于平均水平 → 降低其概率。
• 减少梯度更新的方差（学习更稳定）。

这个简单的基线已经比直接使用原始回报带来了更好的训练效果！它试图权衡整个行动序列与结果（坠毁或降落），从而使策略学会采取能带来更好优势的行动。

经过大量的反复试验，研究人员设计了以下奖励函数。关键在于将奖励同时基于接近度和垂直位置进行条件设定——无人机必须在平台上方才能获得正向奖励，这可以防止智能体利用策略，例如在平台下方盘旋。

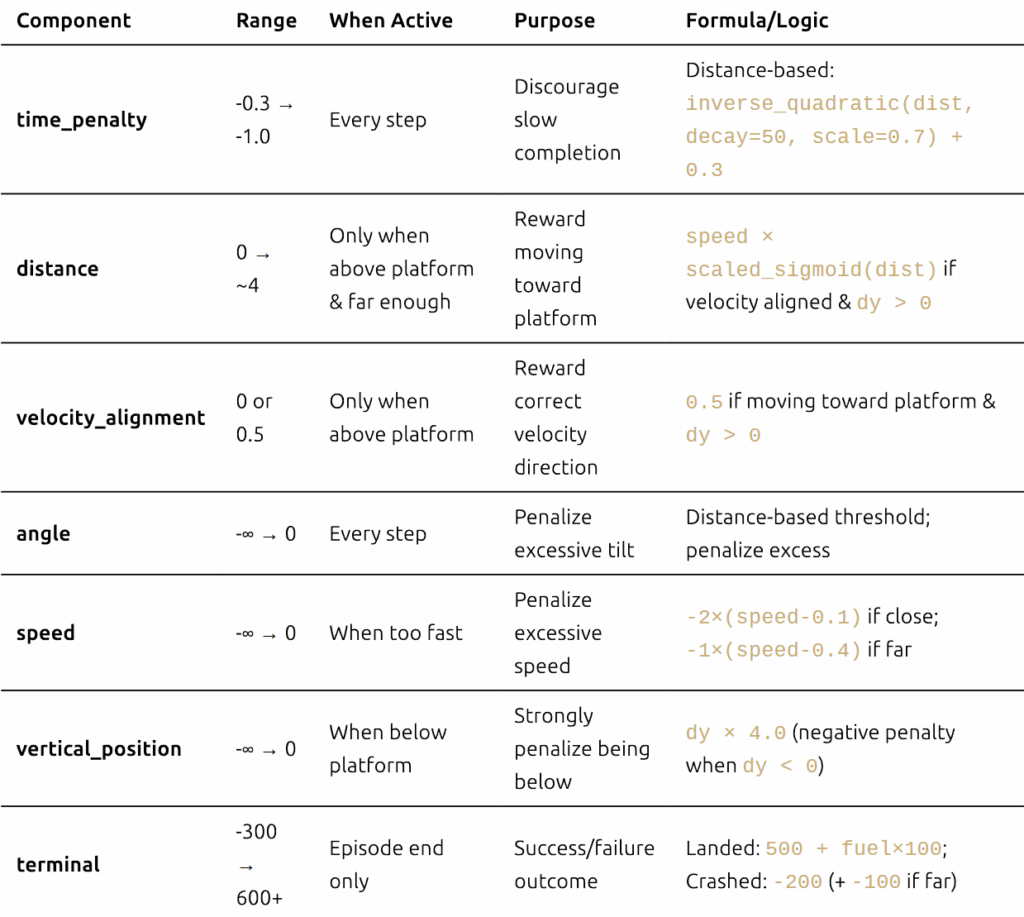
关于反向（非线性）缩放奖励的简短说明

通常，人们希望奖励与某些状态值成反比的行为。例如，到平台的距离范围从 0 到约 1.41（按窗口宽度归一化）。人们希望当距离 ≈ 0 时获得高奖励，而当距离很远时获得低奖励。为此，本文使用了各种缩放函数：

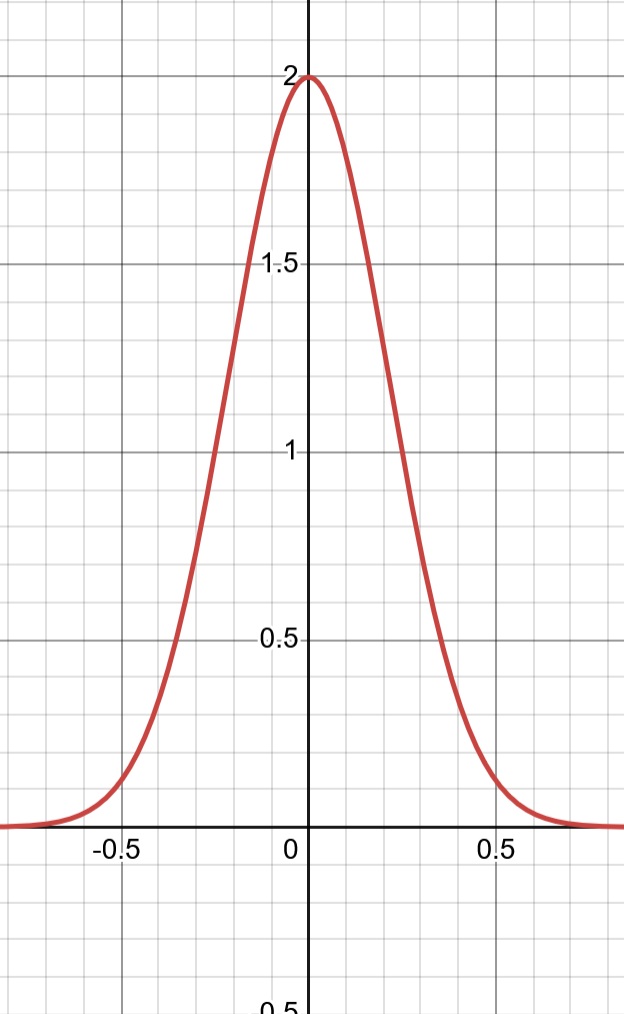
图4. 高斯标量函数

其他有用缩放函数的示例

辅助函数：

def inverse_quadratic(x, decay=20, scaler=10, shifter=0):
    """Reward decreases quadratically with distance"""
    return scaler / (1 + decay * (x - shifter)**2)

def scaled_shifted_negative_sigmoid(x, scaler=10, shift=0, steepness=10):
    """Sigmoid function scaled and shifted"""
    return scaler / (1 + np.exp(steepness * (x - shift)))

def calc_velocity_alignment(state: DroneState):
    """
    Calculate how well the drone's velocity is aligned with optimal direction to platform.
    Returns cosine similarity: 1.0 = perfect alignment, -1.0 = opposite direction
    """
    # Optimal direction: from drone to platform
    optimal_dx = -state.dx_to_platform
    optimal_dy = -state.dy_to_platform
    optimal_norm = math.sqrt(optimal_dx**2 + optimal_dy**2)

    if optimal_norm < 1e-6:  # Already at platform
        return 1.0

    optimal_dx /= optimal_norm
    optimal_dy /= optimal_norm

    # Current velocity direction
    velocity_norm = state.speed
    if velocity_norm < 1e-6:  # Not moving
        return 0.0

    velocity_dx = state.drone_vx / velocity_norm
    velocity_dy = state.drone_vy / velocity_norm

    # Cosine similarity
    return velocity_dx * optimal_dx + velocity_dy * optimal_dy

当前奖励函数的代码：

def calc_reward(state: DroneState):
    rewards = {}
    total_reward = 0

    # 1. Time penalty - distance-based (penalize more when far)
    minimum_time_penalty = 0.3
    maximum_time_penalty = 1.0
    rewards['time_penalty'] = -inverse_quadratic(
        state.distance_to_platform,
        decay=50,
        scaler=maximum_time_penalty - minimum_time_penalty
    ) - minimum_time_penalty
    total_reward += rewards['time_penalty']

    # 2. Distance & velocity alignment - ONLY when above platform
    velocity_alignment = calc_velocity_alignment(state)
    dist = state.distance_to_platform

    rewards['distance'] = 0
    rewards['velocity_alignment'] = 0

    # Key condition: drone must be above platform (dy > 0) to get positive rewards
    if dist > 0.065 and state.dy_to_platform > 0:
        # Reward movement toward platform when velocity is aligned
        if velocity_alignment > 0:
            rewards['distance'] = state.speed * scaled_shifted_negative_sigmoid(dist, scaler=4.5)
            rewards['velocity_alignment'] = 0.5

    total_reward += rewards['distance']
    total_reward += rewards['velocity_alignment']

    # 3. Angle penalty - distance-based threshold
    abs_angle = abs(state.drone_angle)
    max_angle = 0.20
    max_permissible_angle = ((max_angle - 0.111) * dist) + 0.111
    excess = abs_angle - max_permissible_angle
    rewards['angle'] = -max(excess, 0)
    total_reward += rewards['angle']

    # 4. Speed penalty - penalize excessive speed
    rewards['speed'] = 0
    speed = state.speed
    max_speed = 0.4
    if dist < 1:
        rewards['speed'] = -2 * max(speed - 0.1, 0)
    else:
        rewards['speed'] = -1 * max(speed - max_speed, 0)
    total_reward += rewards['speed']

    # 5. Vertical position penalty - penalize being below platform
    rewards['vertical_position'] = 0
    if state.dy_to_platform > 0:  # Drone is above platform (GOOD)
        rewards['vertical_position'] = 0
    else:  # Drone is below platform (BAD!)
        rewards['vertical_position'] = state.dy_to_platform * 4.0  # Negative penalty
    total_reward += rewards['vertical_position']

    # 6. Terminal rewards
    rewards['terminal'] = 0
    if state.landed:
        rewards['terminal'] = 500.0 + state.drone_fuel * 100.0
    elif state.crashed:
        rewards['terminal'] = -200.0
        # Extra penalty for crashing far from target
        if state.distance_to_platform > 0.3:
            rewards['terminal'] -= 100.0
    total_reward += rewards['terminal']

    rewards['total'] = total_reward
    return rewards

是的，那些像4.5、0.065和4.0这样的“神奇数字”？它们是经过大量反复试验才得出的。欢迎来到强化学习的世界，在这里，超参数调整一半是艺术，一半是科学，还有一半是运气（是的，研究人员知道这有三个“一半”）。

def compute_returns(rewards, gamma=0.99):
    """
    Compute discounted returns (G_t) for each timestep based on the Bellman equation

    G_t = r_t + γ*r_{t+1} + γ²*r_{t+2} + ...
    """
    returns = []
    G = 0

    # Compute backwards (more efficient)
    for r in reversed(rewards):
        G = r + gamma * G
        returns.insert(0, G)

    return returns

需要注意的是，奖励函数需要经过仔细的反复试验。如果设计中出现一点错误或奖励过度，智能体就会偏离目标，转而优化那些利用这些错误的行为。这导致了奖励欺骗（Reward Hacking）问题。

奖励欺骗（Reward Hacking）

奖励欺骗发生在智能体找到一种意想不到的方式来最大化奖励，而实际上并未解决期望它解决的任务。智能体并非故意“作弊”——它只是严格按照设定的规则行事，但其行为却并非设计者真正希望的。

经典案例：如果奖励一个清洁机器人“没有可见的灰尘”，它可能会学会关闭摄像头而不是真正清洁！

相关研究人员的经验表明：通过实践深刻体会到这一点。在无人机降落奖励函数的早期版本中，系统对无人机在平台附近“稳定且缓慢”给予积分。听起来很合理，对吗？错了！在 50 个训练回合内，智能体学会了原地盘旋，持续获取免费积分。从技术上讲，这对于设计不当的奖励函数来说是“最优”的——但它真的降落了吗？没有！人们观察到它持续盘旋了 5 分钟，才意识到发生了什么。

以下是当时有问题的代码：

# 请勿复制此代码！
# If drone is above the platform (|dx| < 0.0625) and close (distance < 0.25):
corridor_reward = inverse_quadratic(distance, decay=20, scaler=15)  # Up to 15 points
if stable and slow:
    corridor_reward += 10  # Extra 10 points!
# Total possible: 25 points per step!

奖励欺骗的一个实际示例：

图5. 无人机学会了在平台周围盘旋以获取奖励

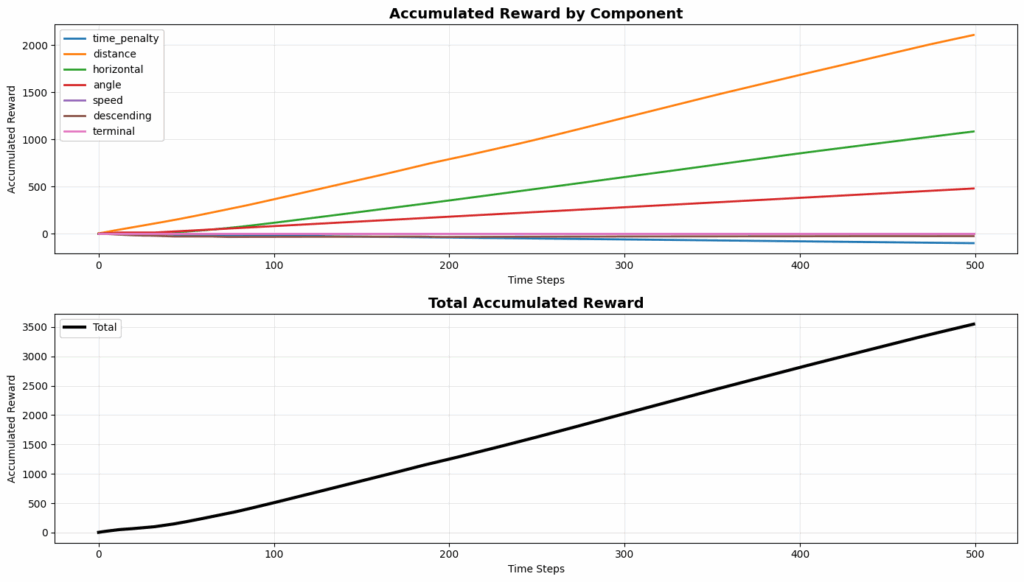
图6. 图表显示无人机明显存在奖励欺骗行为

构建策略网络

如前所述，本文将使用神经网络作为智能体大脑的驱动策略。以下是一个简单的实现，它接收状态向量并计算3 个独立行动的概率分布：

1. 激活主推进器
2. 激活左推进器
3. 激活右推进器

def state_to_array(state):
    """Helper function to convert DroneState dataclass to numpy array"""
    data = np.array([
        state.drone_x,
        state.drone_y,
        state.drone_vx,
        state.drone_vy,
        state.drone_angle,
        state.drone_angular_vel,
        state.drone_fuel,
        state.platform_x,
        state.platform_y,
        state.distance_to_platform,
        state.dx_to_platform,
        state.dy_to_platform,
        state.speed,
        float(state.landed),
        float(state.crashed)
    ])

    return torch.tensor(data, dtype=torch.float32)

class DroneGamerBoi(nn.Module):
    def __init__(self, state_dim=15):
        super().__init__()

        self.network = nn.Sequential(
            nn.Linear(state_dim, 128),
            nn.LayerNorm(128),
            nn.ReLU(),
            nn.Linear(128, 128),
            nn.LayerNorm(128),
            nn.ReLU(),
            nn.Linear(128, 64),
            nn.LayerNorm(64),
            nn.ReLU(),
            nn.Linear(64, 3),
            nn.Sigmoid()
        )

    def forward(self, state):
        if isinstance(state, DroneState):
            state = state_to_array(state)

        return self.network(state)

实际上，不是将行动空间视为 2³ = 8 种组合，而是将其简化为使用伯努利采样对三个独立推进器进行决策。这种简化通过独立处理每个推进器而不是将其视为一个大的分类选择，使得优化更容易（研究人员认为这种方法可能更有效——尽管如此，这种方法确实在实践中取得了效果！）。

---

使用策略梯度训练策略

学习策略：何时进行更新？

一个早期困扰过研究人员的问题是：应该在每一步行动后更新策略，还是等待整个回合结束后再进行更新？事实证明，这个选择非常重要。

如果仅仅基于单个行动获得的奖励进行优化，会导致高方差问题（基本上，训练信号非常嘈杂，梯度指向随机方向！）。所谓“高方差”，是指优化算法在用于更新策略网络参数的梯度中接收到极其混杂的信号。对于同一个行动，系统可能产生一个特定的梯度方向，但对于稍有不同（但行动相同）的状态，却可能产生完全相反的结果。这导致训练缓慢，甚至可能无法进行训练。

有三种方法可以更新策略：

每步更新（Per-Step Updates）

无人机发射一次推进器，获得少量奖励，然后立即更新其整个策略。这就像每次投篮后都调整篮球姿势一样——反应过度！一个幸运的行动增加了奖励，不一定意味着智能体表现良好；一个不幸的行动也不一定意味着智能体表现糟糕。学习信号过于嘈杂。

初次尝试时，研究团队采用了这种方法。无人机会随机摆动，做出一个幸运的动作获得了微小的额外奖励，然后立即过度拟合该特定动作，并反复尝试重现它而坠毁。这个过程令人沮丧——就像看着一个人从纯粹的偶然中学到了错误的教训。

每回合更新（Per-Episode Updates）

这种方法更好！现在，让无人机尝试降落（或坠毁），观察整个尝试的结果，然后更新策略。这就像完成一集后反思如何改进。至少现在可以看到行动的全部后果。但问题是：如果那次降落只是运气好或运气差呢？学习仍然基于单个数据点。

多回合批量更新（Multi-Episode Batch Updates）

这是最佳选择。同时运行多个（例如 6 个）无人机降落尝试，观察它们的整体表现，然后根据平均性能更新策略。有些尝试可能运气好，有些可能运气差，但平均下来，可以得到更清晰的有效策略。尽管这种方法对计算机的计算量较大，但如果能够运行，它的效果远优于前两种方法。当然，这种方法并非最佳，但它非常易于理解和实现；还有其他（更好）的方法。

以下是游戏中收集多个回合的代码：

def collect_episodes(client: DroneGameClient, policy: nn.Module, max_steps=300):
    """
    Collect episodes with early stopping

    Args:
        client: The game's socket client
        policy: PyTorch module
        max_steps: Maximum steps per episode (default: 300)
    """
    num_games = client.num_games

    # Initialize storage
    all_episodes = [{'states': [], 'actions': [], 'log_probs': [], 'rewards': [], 'done': False}
                    for _ in range(num_games)]

    # Reset all games
    game_states = [client.reset(game_id) for game_id in range(num_games)]
    step_counts = [0] * num_games  # Track steps per game

    while not all(ep['done'] for ep in all_episodes):
        # Batch active games
        batch_states = []
        active_game_ids = []

        for game_id in range(num_games):
            if not all_episodes[game_id]['done']:
                batch_states.append(state_to_array(game_states[game_id]))
                active_game_ids.append(game_id)

        if len(batch_states) == 0:
            break

        # Batched inference
        batch_states_tensor = torch.stack(batch_states)
        batch_action_probs = policy(batch_states_tensor)
        batch_dist = Bernoulli(probs=batch_action_probs)
        batch_actions = batch_dist.sample()
        batch_log_probs = batch_dist.log_prob(batch_actions).sum(dim=1)

        # Execute actions
        for i, game_id in enumerate(active_game_ids):
            action = batch_actions[i]
            log_prob = batch_log_probs[i]

            next_state, _, done, _ = client.step({
                "main_thrust": int(action[0]),
                "left_thrust": int(action[1]),
                "right_thrust": int(action[2])
            }, game_id)

            reward = calc_reward(next_state)

            # Store data
            all_episodes[game_id]['states'].append(batch_states[i])
            all_episodes[game_id]['actions'].append(action)
            all_episodes[game_id]['log_probs'].append(log_prob)
            all_episodes[game_id]['rewards'].append(reward['total'])

            # Update state and step count
            game_states[game_id] = next_state
            step_counts[game_id] += 1

            # Check done conditions
            if done or step_counts[game_id] >= max_steps:
                # Apply timeout penalty if hit max steps without landing
                if step_counts[game_id] >= max_steps and not next_state.landed:
                    all_episodes[game_id]['rewards'][-1] -= 500  # Timeout penalty

                all_episodes[game_id]['done'] = True

    # Return episodes
    return [(ep['states'], ep['actions'], ep['log_probs'], ep['rewards'])
            for ep in all_episodes]

最大化-最小化难题

在典型的深度学习（监督学习）中，人们会最小化一个损失函数：

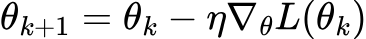
目标是“下坡”走向更低的损失（更好的预测）。

但在强化学习中，人们希望最大化总奖励！目标是：

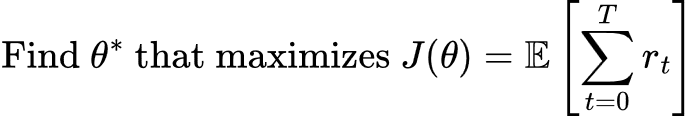
问题在于：深度学习框架是为最小化而不是最大化而构建的。如何将“最大化奖励”转化为“最小化损失”呢？

简单的技巧：最大化 J(θ) = 最小化 -J(θ)

所以损失函数变为：

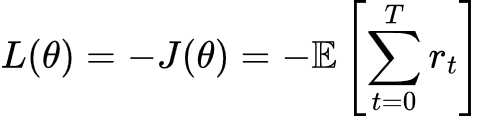
现在，梯度下降将沿着奖励景观“向上攀爬”（更像是梯度上升），因为它沿着负奖励方向下降！

REINFORCE 算法（策略梯度）

策略梯度定理（Williams, 1992）告诉了人们如何计算期望奖励的梯度：

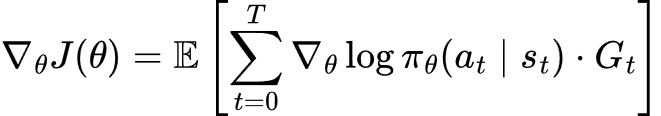
（尽管这看起来有些复杂，但深入理解后会发现其精妙之处！）

其中：

用通俗易懂的语言来说（因为那个公式太抽象了）：

• 如果行动a t带来了高回报G t，则增加其概率。
• 如果行动a t带来了低回报G t，则降低其概率。
• 梯度指明了调整神经网络权重方向。

添加基线（减少方差）

使用原始回报G t会导致高方差（噪声梯度）。通过减去一个基线 b(s t) 来改进这一点：

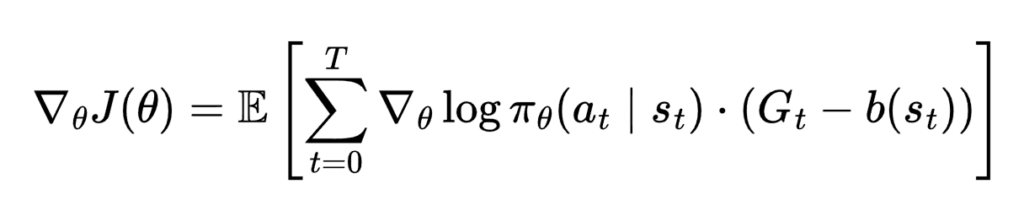
最简单的基线是平均回报：

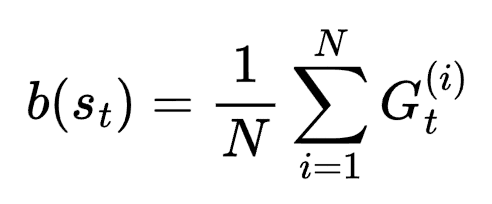
这给出了优势：A t = G t – b

• 正向优势 → 行动优于平均水平 → 增加概率。
• 负向优势 → 行动劣于平均水平 → 降低概率。

这为什么有帮助：不再是“这个行动获得了 100 点奖励”（这算好吗？），而是“这个行动获得了 100 点奖励，而平均水平是 50 点”（那太棒了！）。相对表现比绝对表现更清晰。

我们的实现

在无人机降落代码中，使用了带有基线的REINFORCE 算法：

# 1. Collect episodes and compute returns
returns = compute_returns(rewards, gamma=0.99)  # G_t with discounting

# 2. Compute baseline (mean of all returns)
baseline = returns_tensor.mean()

# 3. Compute advantages
advantages = returns_tensor - baseline

# 4. Normalize advantages (extra variance reduction)
advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)

# 5. Compute loss (note the negative sign!)
loss = -(log_probs_tensor * advantages).mean()

# 6. Gradient descent
optimizer.zero_grad()
loss.backward()
optimizer.step()

上述循环将重复多次，直到无人机学会正确降落。有关更多代码，请查看这个 Jupyter Notebook！

当前成果（奖励函数仍存在缺陷）

经过无数小时的奖励函数调整、超参数优化以及观察智能体以各种意想不到的方式坠毁，团队最终使其得以运行（大部分情况下）。尽管设计的奖励函数并非完美，但它确实能够训练出一个策略网络。以下是一个成功的降落示例：

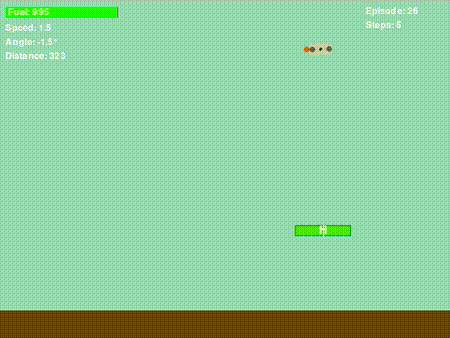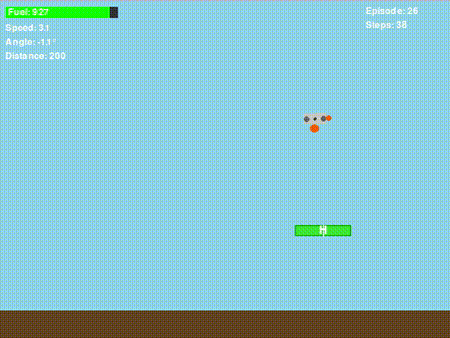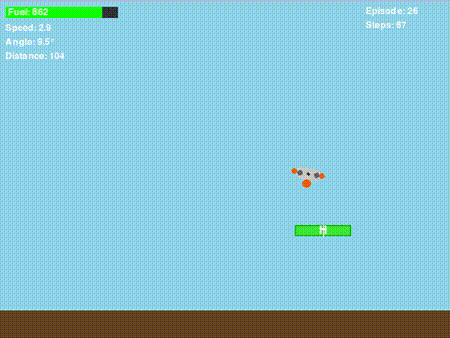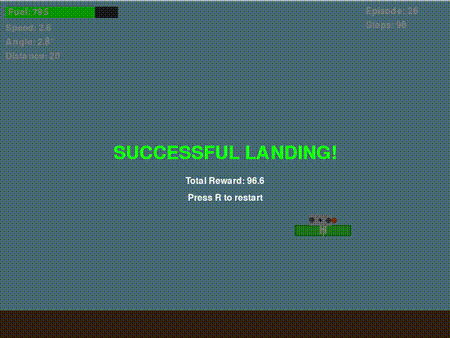
图6. 无人机学到了一些东西！

这相当酷，不是吗？但接下来的情况变得有趣（也令人沮丧）……

---

持续盘旋问题：一个根本性局限

即使改进了奖励函数，将其条件设定为基于垂直位置（dy_to_platform > 0），训练出的策略仍然表现出一种令人沮丧的行为：当无人机未能成功降落到平台上时，它会学会向下朝平台方向移动，但随后却在平台下方盘旋，而非尝试降落。

研究团队花费了一周多的时间观察奖励曲线（并修改奖励函数），思考为何“修正后”的奖励函数仍然导致这种盘旋行为。当最终绘制出累积奖励图时，这种模式变得清晰可见——坦率地说，研究人员甚至无法对智能体找到这种策略感到生气。

发生了什么？

通过分析无人机在平台下方盘旋的回合中累积的奖励，发现了一些有趣现象：

图7. GIF动图显示“平台下方盘旋”问题

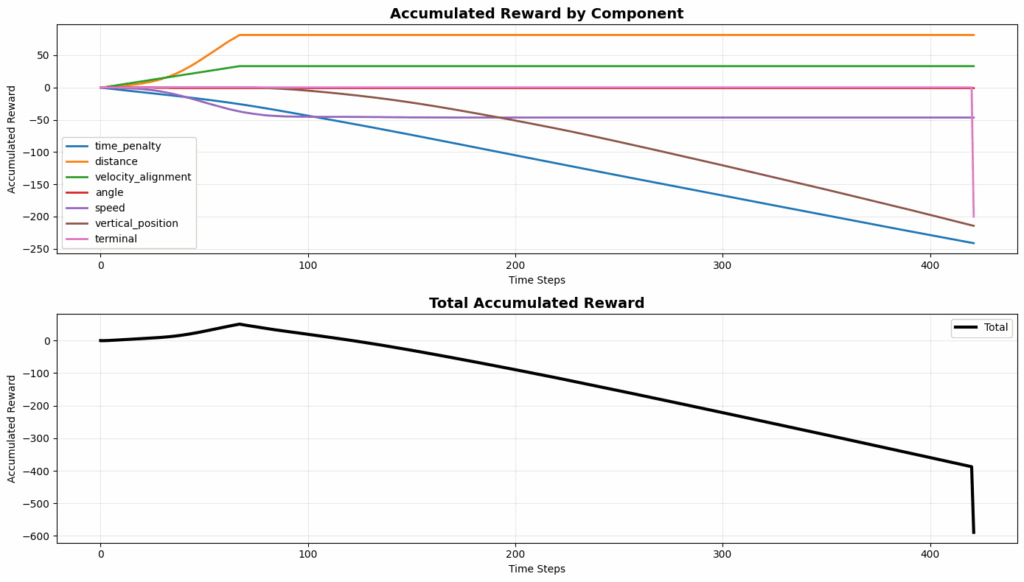
图8. 图表显示无人机明显存在奖励欺骗行为

图表揭示：

• 距离奖励（橙色）：早期累积到约 +70，随后趋于平稳（不再获得奖励）。
• 速度对齐奖励（绿色）：早期累积到约 +30，随后趋于平稳。
• 时间惩罚（蓝色）：稳步累积到约 -250（持续恶化）。
• 垂直位置惩罚（棕色）：稳步累积到约 -200（低于平台的惩罚）。
• 总奖励：最终在 -400 到 -600 之间（超时后）。

关键洞察：无人机从平台上方下降（在下降过程中收集距离和速度奖励），穿过平台高度，然后选择在下方盘旋而不是完成降落。一旦在下方，它就会停止获得正向奖励（注意距离和速度曲线在大约 50-60 步时趋于平稳），但会继续累积时间惩罚和垂直位置惩罚。然而，这种策略仍然可行，因为尝试降落有立即获得 -200 坠毁惩罚的风险，而下方盘旋在整个回合中“仅”花费约 -400 到 -600。这种权衡导致智能体选择了次优行为。

为什么会发生这种情况？

根本问题在于，奖励函数r(s', a)只能看到当前状态，而无法感知轨迹。想想看：在任何一个时间步，奖励函数无法区分以下两种情况：

• 一架正在朝降落方向前进的无人机（从上方以受控方式下降）。
• 一架正在利用奖励结构的无人机（通过振荡来获取奖励）。

两者在给定时刻都可能满足dy_to_platform > 0，因此它们会获得相同的奖励！智能体并不愚蠢——它只是精确地优化了被告知要优化的内容。

那么，真正解决这个问题的方法是什么？

为了真正解决这个问题，研究人员认为奖励应该依赖于状态转换：r(s, a, s')而不是仅仅r(s, a)。这将允许奖励基于（s 为当前状态，s’ 为下一状态）：

• 进展：仅当distance(s') < distance(s)时给予奖励（确实在靠近！）。
• 垂直改善：仅当无人机相对于平台持续向上移动时给予奖励。
• 轨迹一致性：惩罚指示振荡的快速方向变化。

这比试图通过日益严厉的惩罚来修补当前奖励函数（这正是研究人员尝试了一段时间但并未奏效的方法）更为原则性的解决方案。振荡利用之所以存在，是因为人们从根本上缺失了关于轨迹的信息。

在下一篇文章中，研究人员将探讨Actor-Critic 方法和可以融入时间信息以防止这些利用策略的技术。敬请期待！

如果您有解决方案，欢迎与相关研究人员交流！

至此，关于“深度强化学习最简方法”的探讨告一段落。

---

下一步计划

• Actor-Critic 系统
• DQL (深度 Q 学习)
• PPO & GRPO (近端策略优化 & 广义优势估计)
• 将其应用于需要视觉识别的系统

---

参考文献

基础理论

1. Turing, A. M.(1950). “Computing Machinery and Intelligence.”

   • 图灵测试原始论文

2. Williams, R. J.(1992). “Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning.”Machine Learning.

   • REINFORCE 算法

3. Sutton, R. S., & Barto, A. G.(2018).Reinforcement Learning: An Introduction. MIT Press.

   • 基础教科书
   • 免费在线阅读：http://incompleteideas.net/book/the-book-2nd.html

经典条件反射与行为心理学

1. Pavlov, I. P.(1927).Conditioned Reflexes: An Investigation of the Physiological Activity of the Cerebral Cortex. Oxford University Press.

   • 经典条件反射实验

2. Skinner, B. F.(1938).The Behavior of Organisms: An Experimental Analysis. Appleton-Century-Crofts.

   • 操作性条件反射与斯金纳箱

策略梯度方法

1. Sutton, R. S., McAllester, D., Singh, S., & Mansour, Y.(1999). “Policy Gradient Methods for Reinforcement Learning with Function Approximation.”Advances in Neural Information Processing Systems.

   • 策略梯度的理论基础

2. Schulman, J., Moritz, P., Levine, S., Jordan, M., & Abbeel, P.(2015). “High-Dimensional Continuous Control Using Generalized Advantage Estimation.”arXiv preprint arXiv:1506.02438.

神经网络与深度学习

1. Goodfellow, I., Bengio, Y., & Courville, A.(2016).Deep Learning. MIT Press.
   • 神经网络基础参考书
   • 在线阅读：https://www.deeplearningbook.org/

在线资源

1. Karpathy, A.“Deep Reinforcement Learning: Pong from Pixels.”

   • 博客文章：http://karpathy.github.io/2016/05/31/rl/
   • 具有影响力的教育资源

2. Spinning Up in Deep RLby OpenAI

   • 教育资源：https://spinningup.openai.com/
   • 出色的策略梯度解释

代码库

1. Jumle, V.(2025). “Reinforcement Learning 101: Delivery Drone Landing.”
   • GitHub：https://github.com/vedant-jumle/reinforcement-learning-101

致谢

1. Singh, Navroop Kaur.(2025): 感谢提供“积极氛围与关注”。