若您错过了本系列第一部分:《如何评估 RAG 管道中的检索质量》,请点击此处查看。
在之前的文章中,探讨了 RAG(检索增强生成)管道的检索质量评估方法及一些基础指标。具体来说,本系列的第一部分主要关注了二元、与顺序无关的评估指标,主要判断检索结果集中是否存在相关内容。而在本系列的第二部分,本文将进一步深入探讨二元、与顺序相关的评估指标。这类指标不仅评估相关结果是否存在,还会考虑每个相关结果被检索到的排名。因此,本文将详细介绍两种常用的二元、与顺序相关的评估指标:平均倒数排名(Mean Reciprocal Rank, MRR)和平均精确率(Average Precision, AP)。
为何检索评估中排名如此重要?
在 RAG 管道中,高效的检索机制至关重要,因为它是在文档基础上生成有效答案的第一步。如果无法首先识别出包含所需信息的正确文档,任何人工智能的“魔法”都无法弥补这一缺陷并提供准确的答案。
检索质量评估指标大致可分为两大类:二元评估指标和分级评估指标。具体而言,二元评估指标将检索到的文本块简单地归类为相关或不相关,没有中间状态。另一方面,当使用分级评估指标时,会将文本块与用户查询的相关性视为一个连续的谱系,因此检索到的文本块可以有不同程度的相关性。
二元评估指标又可进一步细分为与顺序无关和与顺序相关的指标。与顺序无关的指标仅评估检索结果集中是否存在某个文本块,而不考虑其被检索到的排名。在之前的文章中(本系列第一部分),详细探讨了最常见的二元、与顺序无关的评估指标,并通过 Python 代码示例进行了深入分析,包括命中率@K(HitRate@K)、精确率@K(Precision@K)、召回率@K(Recall@K)和F1@K。相比之下,二元、与顺序相关的评估指标除了考虑文本块是否存在于检索结果集中外,还会考虑其被检索到的排名。
因此,在本文中,将更详细地探讨最常用的二元、与顺序相关的检索指标,例如 MRR 和 AP,并展示如何在 Python 中计算这些指标。
一些与顺序相关的二元评估指标
与顺序无关的二元评估指标,例如精确率@K或召回率@K,只能告诉我们相关文档是否存在于前 k 个结果中,但无法指出该文档是排在靠前还是靠后的位置。而这正是与顺序相关的评估指标所能提供的精确信息。一些非常有用且常用的与顺序相关的评估指标包括平均倒数排名(Mean Reciprocal Rank, MRR)和平均精确率(Average Precision, AP)。下面将对这些指标进行更详细的探讨。
 平均倒数排名 (MRR)
平均倒数排名 (MRR)
评估检索质量的常用顺序感知指标之一是平均倒数排名(MRR)。回顾一下,倒数排名(Reciprocal Rank, RR)表示在检索到的前 k 个结果中,第一个真正相关的结果出现在哪个排名位置。更准确地说,它衡量了第一个相关结果在排名中的位置有多高。RR 可以按如下方式计算,其中 rank_i 是第一个相关结果被发现的排名:
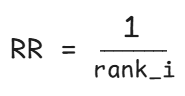
图片由作者提供
也可以通过以下示例直观地了解此计算过程:

图片由作者提供
现在可以综合理解平均倒数排名(MRR)。MRR 表示在不同结果集中,第一个相关项的平均位置。
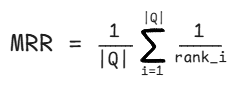
图片由作者提供
通过这种方式,MRR 的取值范围在 0 到 1 之间。也就是说,MRR 值越高,第一个相关文档在排名中的位置就越靠前。
一个现实生活中的例子可以说明 MRR 在评估 RAG 管道检索步骤中的用处:在任何快节奏的环境中,都需要快速决策,并确保一个真正相关的结果能够迅速浮现在搜索结果的顶部。MRR 对于评估那些只需一个相关结果就足够,且重要信息不分散在多个文本块中的系统非常有效。
为了更好地理解 MRR 这一检索评估指标,一个很好的比喻是谷歌搜索。用户认为谷歌是一个优秀的搜索引擎,正是因为能够在其顶部结果中找到所需内容。如果用户必须滚动到第 150 个结果才能找到所需信息,那么就不会认为它是一个好的搜索引擎。同样,RAG 管道中优秀的向量搜索机制也应该能够将相关文本块呈现在相对靠前的排名位置,从而获得较高的 MRR 分数。
 平均精确率 (AP)
平均精确率 (AP)
在讨论二元、与顺序无关的检索评估指标时,本系列第一部分曾专门探讨了精确率@k(Precision@k)。具体来说,精确率@k 表示在前 k 个检索到的文档中有多少是真正相关的。精确率@k 的计算方式如下:
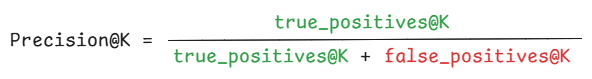
图片由作者提供
平均精确率(Average Precision, AP)在此基础上进一步发展。具体来说,要计算 AP,需要首先迭代计算每个新相关项出现时的精确率@k。然后,通过简单地计算这些精确率@k 分数的平均值,即可得到 AP。
为了更好地理解这一计算,以下是一个示例。对于此示例集,可以观察到,当 k=1 和 k=4 时,检索结果中出现了新的相关文本块。
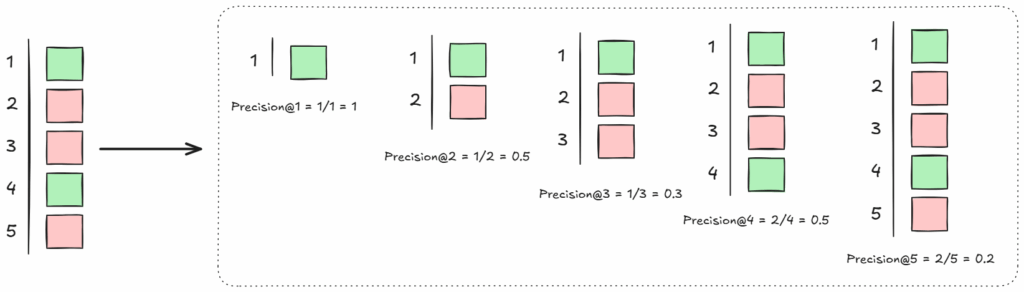
图片由作者提供
因此,计算 Precision@1 和 Precision@4,然后取它们的平均值。即 (1/1 + 2/4) / 2 = (1 + 0.5) / 2 = 0.75。
平均精确率的计算可以泛化为:

图片由作者提供
同样,AP 的取值范围也在 0 到 1 之间。具体来说,AP 分数越高,表明检索系统将相关文档排名靠前的能力越强。换句话说,这意味着检索到的相关文档越多,并且它们在不相关文档之前出现的频率也越高。
与 MRR 仅关注第一个相关结果不同,AP 考虑了所有检索到的相关文本块的排名。它本质上量化了在检索真正相关项目时,不同 k 值下所获得的“垃圾”信息量有多少。
为了更好地理解 AP 和 MRR,可以将其想象成一个 Spotify 播放列表。与谷歌搜索的例子类似,高 MRR 意味着播放列表的第一首歌就是用户最喜欢的歌曲。另一方面,高 AP 则意味着整个播放列表都很好,许多用户喜欢的歌曲频繁出现且排名靠前。
那么,向量搜索效果如何?
通常,评估 RAG 管道的检索性能会结合实际案例进行深入探讨,例如在其他 RAG 教程中使用的《战争与和平》示例。然而,完整的检索代码会变得相当庞大,不便在每篇文章中都包含。因此,本文将重点展示如何在 Python 中计算这些指标,并尽量保持示例的简洁性。
接下来,本文将展示如何在 Python 中实践计算 RAG 管道的 MRR 和 AP。倒数排名(RR)和平均倒数排名(MRR)的计算函数可以定义如下:
from typing import List, Iterable, Sequence
# Reciprocal Rank (RR) - 倒数排名
def reciprocal_rank(relevance: Sequence[int]) -> float:
for i, rel in enumerate(relevance, start=1):
if rel:
return 1.0 / i
return 0.0
# Mean Reciprocal Rank (MRR) - 平均倒数排名
def mean_reciprocal_rank(all_relevance: Iterable[Sequence[int]]) -> float:
vals = [reciprocal_rank(r) for r in all_relevance]
return sum(vals) / len(vals) if vals else 0.0
在第一部分中,已对 精确率@k(Precision@k)进行了计算,其定义如下:
# Precision@k - 精确率@k
def precision_at_k(relevance: Sequence[int], k: int) -> float:
k = min(k, len(relevance))
if k == 0:
return 0.0
return sum(relevance[:k]) / k
在此基础上,平均精确率(AP)可以定义如下:
def average_precision(relevance: Sequence[int]) -> float:
if not relevance:
return 0.0
precisions = []
hit_count = 0
for i, rel in enumerate(relevance, start=1):
if rel:
hit_count += 1
precisions.append(hit_count / i) # Precision@i - 精确率@i
return sum(precisions) / hit_count if hit_count else 0.0
这些函数都以一个二元相关性标签列表作为输入,其中 1 表示检索到的文本块与查询相关,0 表示不相关。在实践中,这些标签是通过将检索结果与真实数据集进行比较来生成的,与本系列第一部分计算精确率@K和召回率@K的方法一致。通过这种方式,对于每个查询(例如,“安娜·帕夫洛夫娜是谁?”),可以根据每个检索到的文本块是否包含答案文本来生成一个二元相关性列表。然后,便可以使用上述函数计算所有指标。
另一个有用的顺序感知指标是平均平均精确率(Mean Average Precision, MAP)。可以想象,MAP 是针对不同检索结果集的平均精确率(AP)的平均值。例如,如果对 RAG 管道中的三个不同测试问题计算 AP,那么 MAP 分数将反映所有这些问题的整体排名质量。
总结与展望
本系列第一部分讨论的二元、与顺序无关的评估指标,例如命中率@k、精确率@k、召回率@k和F1@k,能够为评估 RAG 管道的检索性能提供有价值的信息。然而,这些度量仅提供了相关文档是否存在于检索结果集中的信息。
本文回顾的二元、与顺序相关的评估指标,如平均倒数排名(MRR)和平均精确率(AP),则能提供更深入的见解。它们不仅揭示了相关文档是否存在于检索结果中,还评估了它们的排名质量。通过这种方式,可以根据任务和所使用的文档类型,更好地评估 RAG 管道的检索机制性能。
敬请期待本检索评估系列的下一部分,届时将深入探讨 RAG 管道的分级检索评估方法。