在上一篇文章中,探讨了决策树回归器如何通过最小化均方误差来选择最优分割点。
本文作为机器学习系列文章的第七篇,将延续相同思路,聚焦于决策树回归器的分类对应物——决策树分类器。
通过两个简单数据集快速建立直觉
首先从一个非常小的模拟数据集开始,该数据集包含一个数值特征和一个包含0和1两个类别的目标变量。
核心思路是基于一条规则将数据集一分为二。但关键问题是:这条规则应该是什么? 评判哪个分割更好的标准又是什么?
即使暂时不了解背后的数学原理,也可以直接观察数据并猜测可能的分割点。
从视觉上看,8 或 12 似乎是合理的候选点。
但问题在于,从数值上哪个点更合适。
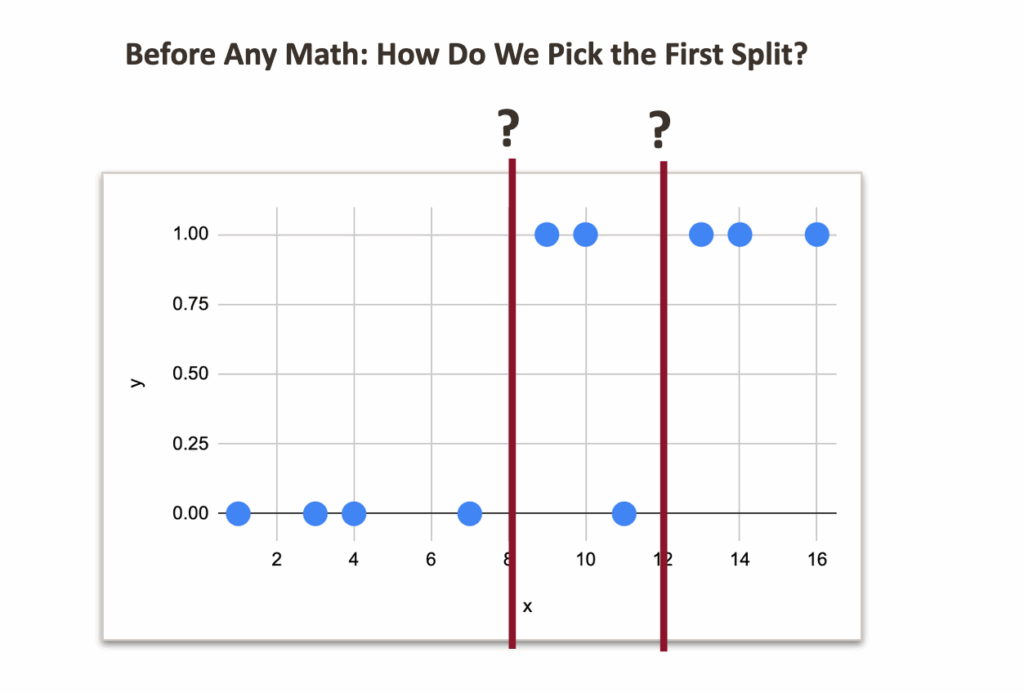
决策树分类器在Excel中的示例 – 图片由作者提供
直观分析如下:
-
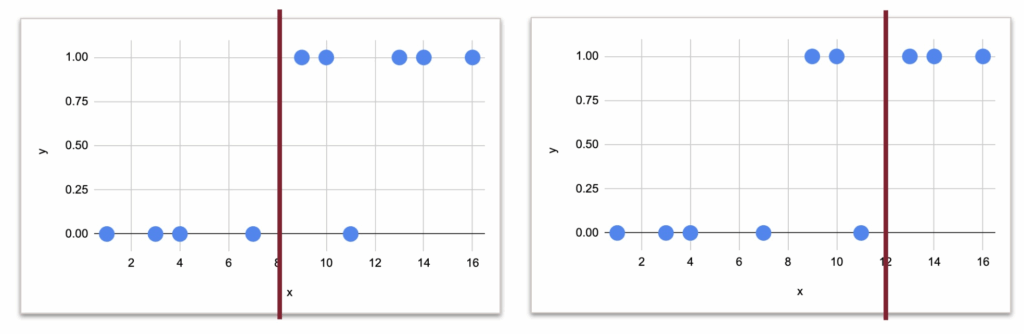
在 8 处分割:
- 左侧:无错误分类
- 右侧:一个错误分类
-
在 12 处分割:
- 右侧:无错误分类
- 左侧:两个错误分类
因此,在8处分割显然感觉更好。
接下来,观察一个包含三个类别的例子。添加了一些随机数据,并创建了3个类别。
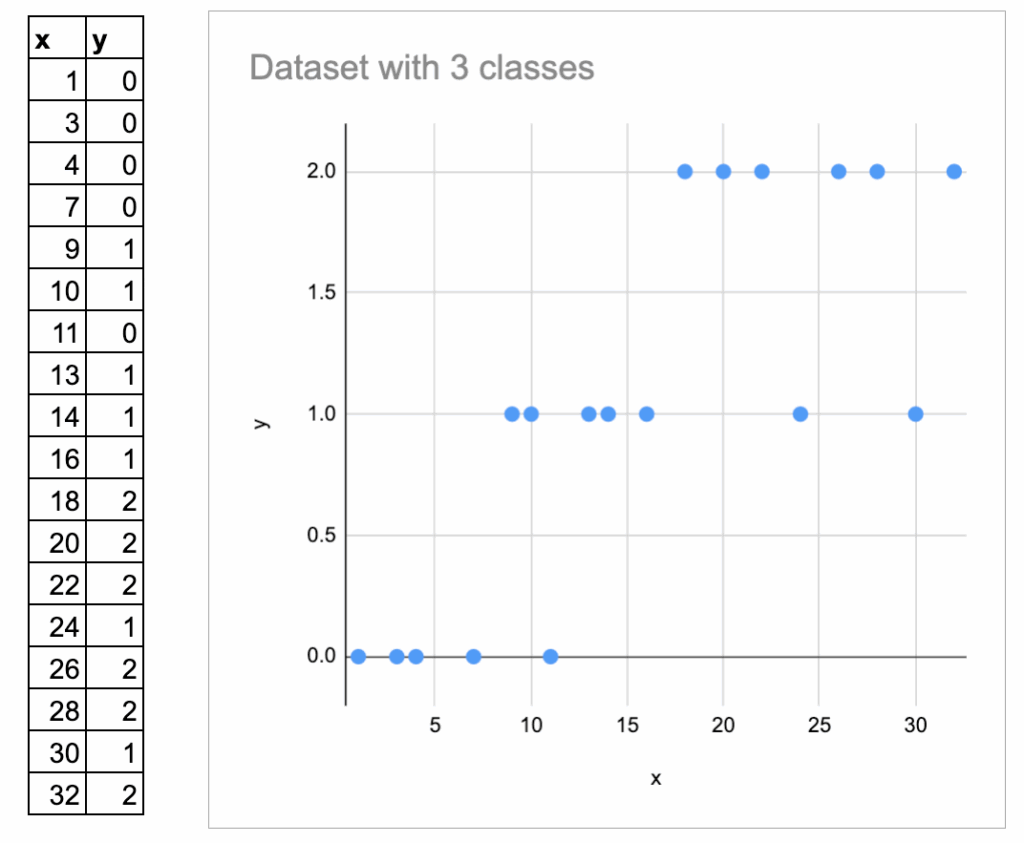
这里将它们标记为0, 1, 3,并垂直绘制。
但需要注意:这些数字仅是类别名称,而非数值。不应将其视为“有序”的。
因此,核心直觉始终是:分割后每个区域的同质性如何?
然而,仅凭视觉判断最佳分割点变得更加困难。
此时,就需要一种数学方法来量化这一思想。
这正是下一章节的主题。
以不纯度度量作为分割标准
在决策树回归器中,已知:
- 一个区域的预测值是目标变量的平均值。
- 分割质量通过均方误差来衡量。
在决策树分类器中:
- 一个区域的预测值是该区域的多数类。
- 分割质量通过不纯度度量来衡量:基尼不纯度或信息熵。
这两者在教科书中都是标准方法,并且在scikit-learn中均可使用。默认使用的是基尼不纯度。
但是,这个不纯度度量究竟是什么?
观察基尼和熵的曲线,它们的行为模式相同:
- 当节点纯净时(所有样本属于同一类),它们的值为0。
- 当类别均匀混合时(各占50%),它们达到最大值。
- 曲线平滑、对称,并随着“混乱度”增加而上升。
这是任何不纯度度量的本质属性:
当组内纯净时,不纯度低;当组内混合时,纯度高。
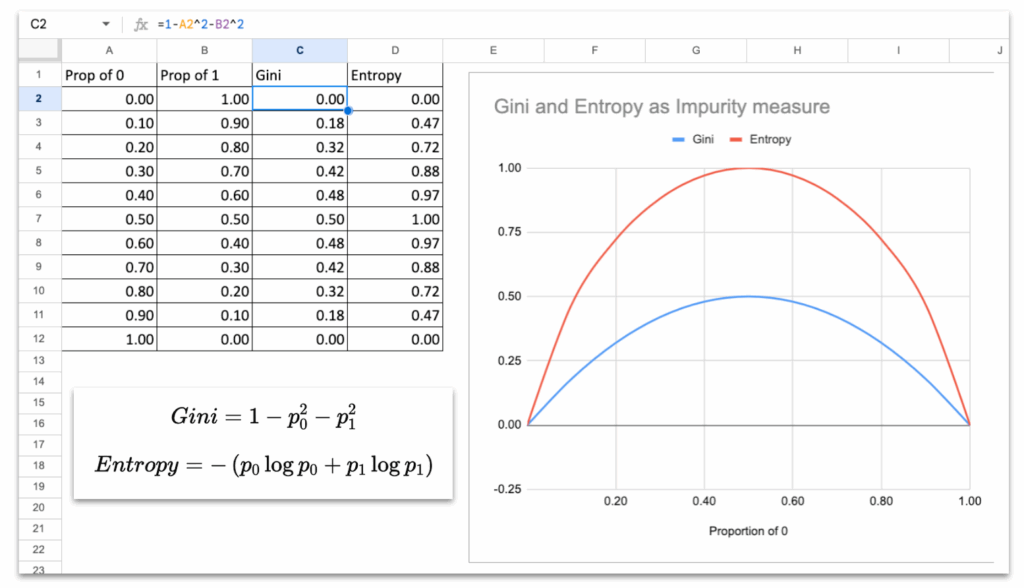
决策树分类器中的基尼不纯度与信息熵 – 图片由作者提供
因此,将使用这些度量来决定创建哪个分割。
基于单个连续特征进行分割
与决策树回归器类似,将遵循相同的结构。
列出所有可能的分割点
与回归器版本完全相同,对于一个数值特征,需要测试的唯一分割点是连续排序后的x值之间的中点。
为每个分割点计算两侧的不纯度
以一个分割值为例,例如 x = 5.5。
将数据集分成两个区域:
- 区域 L:x < 5.5
- 区域 R:x ≥ 5.5
对于每个区域:
- 统计观察点的总数
- 计算基尼不纯度
- 最后,计算分割的加权不纯度
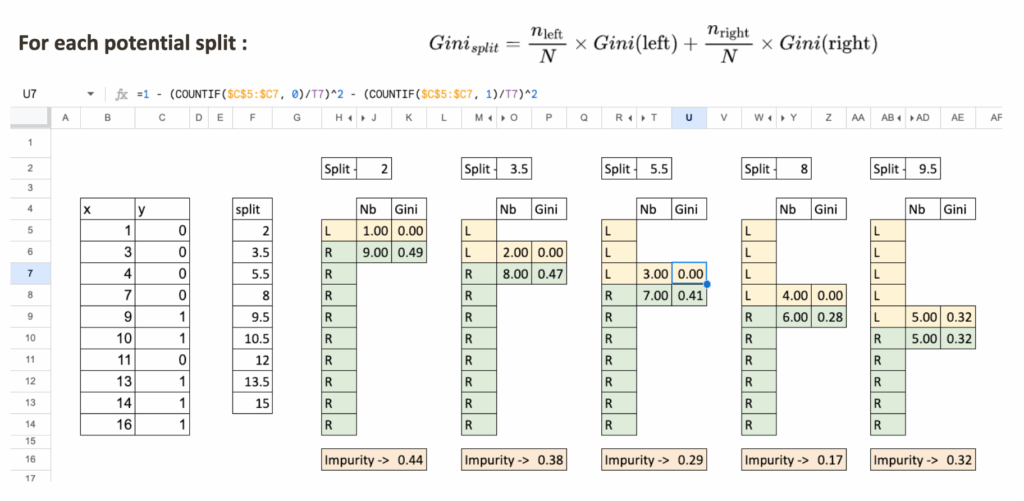
决策树分类器在Excel中的计算示例 – 图片由作者提供
选择不纯度最低的分割点
与回归器的情况类似:
- 列出所有可能的分割点
- 计算每个分割点的不纯度
- 最优分割点是不纯度最小的那个
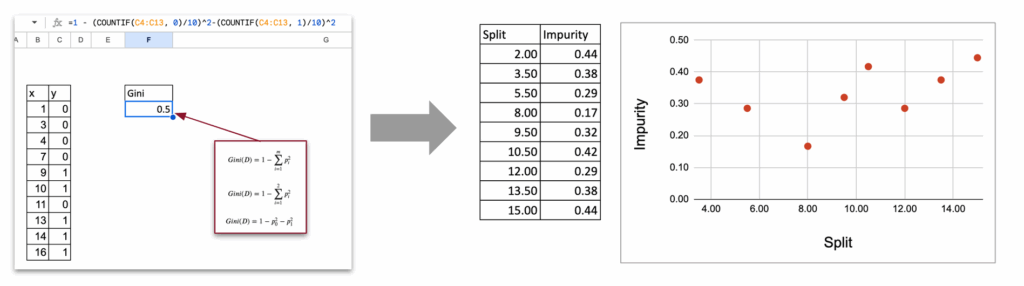
决策树分类器在Excel中选择最优分割点 – 图片由作者提供
所有分割点的综合表格
为了在Excel中实现全自动化计算,
将所有计算组织在一个表格中,其中:
- 每一行对应一个候选分割点,
- 对于每一行,计算:
- 左侧区域的基尼不纯度,
- 右侧区域的基尼不纯度,
- 以及分割的总体加权基尼不纯度。
该表格清晰、紧凑地展示了所有可能的分割点,
而最佳分割点就是最后一列中数值最小的那个。
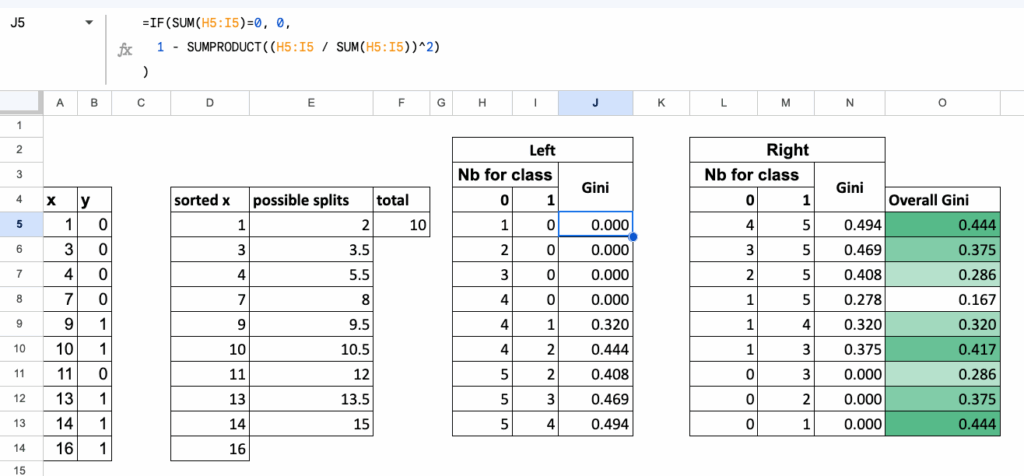
决策树分类器在Excel中的综合计算表 – 图片由作者提供
多类别分类
到目前为止,讨论的是两个类别。但基尼不纯度可以自然地扩展到三个类别,而分割的逻辑则完全保持不变。
算法的结构没有任何变化:
- 列出所有可能的分割点,
- 计算每一侧的不纯度,
- 取加权平均值,
- 选择不纯度最低的分割点。
只有基尼不纯度的公式会稍微变长一些。
三类别下的基尼不纯度
如果一个区域包含三个类别的比例分别为 p1, p2, p3,
那么基尼不纯度为:
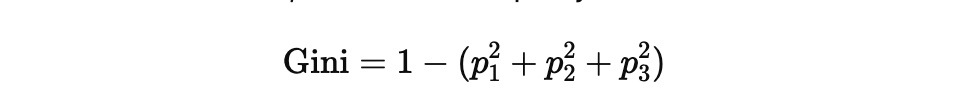
核心思想与之前相同:
当一个类别占主导地位时,区域是“纯净”的,
而当类别混合时,不纯度会变大。
左侧和右侧区域
对于每个分割点:
- 区域 L 包含类别 1、2 和 3 的一些观察点
- 区域 R 包含剩余的观察点
对于每个区域:
- 统计属于每个类别的点数
- 计算比例 p1, p2, p3
- 使用上述公式计算基尼不纯度
所有步骤都与二分类情况完全相同,只是多了一项。
三类别分割汇总表
与之前一样,将所有计算收集在一个表格中:
- 每一行是一个可能的分割点
- 统计左侧的类别1、类别2、类别3的数量
- 统计右侧的类别1、类别2、类别3的数量
- 计算左侧基尼、右侧基尼以及加权基尼
具有最小加权不纯度的分割点就是决策树选择的分割点。
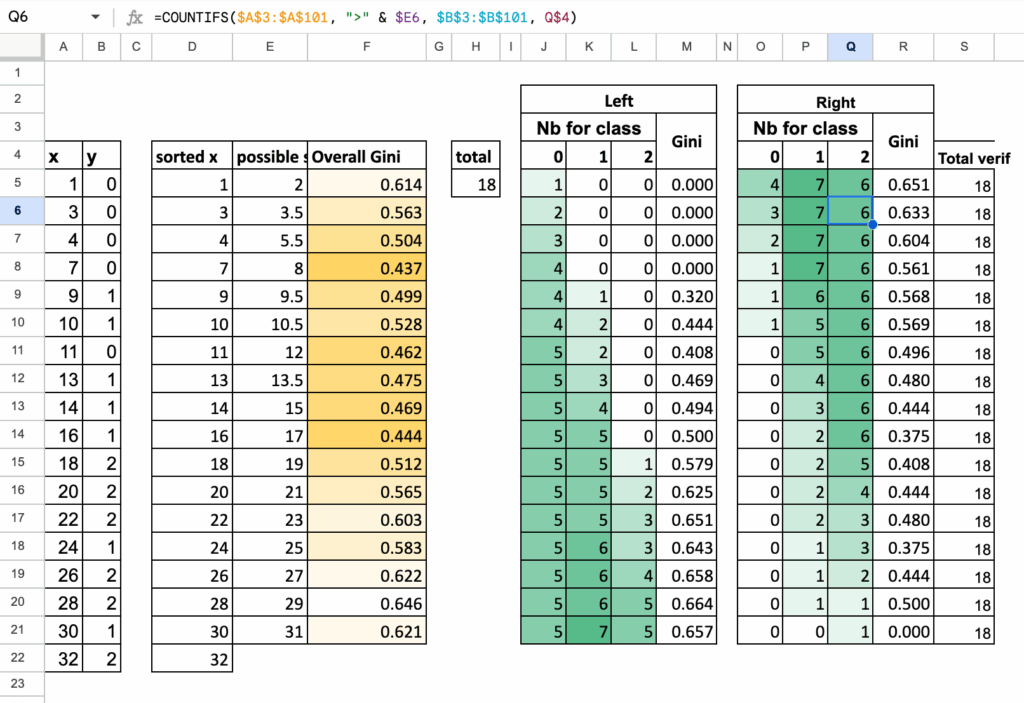
决策树分类器在Excel中的三类别分割计算 – 图片由作者提供
可以轻松地将算法推广到K个类别,使用以下公式计算基尼不纯度或信息熵。

决策树分类器在Excel中的多类别不纯度计算 – 图片由作者提供
不同不纯度度量的实际差异有多大?
虽然总是提到基尼或熵作为标准,但它们真的不同吗? 观察数学公式,有人可能会问。
答案是否定的,差异不大。
理论上,在几乎所有实际情况下:
- 基尼和熵会选择相同的分割点
- 树的结构几乎相同
- 预测结果相同
为什么?
因为它们的曲线看起来极其相似。
它们都在50%混合度时达到峰值,并在纯净时降至零。
唯一的区别是曲线的形状:
- 基尼是一个二次函数。它对错误分类的惩罚更线性。
- 熵是一个对数函数,因此在接近0.5时对不确定性的惩罚稍强一些。
但实际差异很小,并且可以在Excel中进行验证!
其他不纯度度量?
另一个自然的问题是:是否可能发明/使用其他度量?
是的,可以自定义函数,只要它满足:
- 当节点纯净时,值为0
- 当类别混合时,值为最大
- 在“混乱度”增加时平滑且严格递增
例如:不纯度 = 4 * p0 * p1
这是另一个有效的不纯度度量。当只有两个类别时,它实际上等于基尼乘以一个常数。
因此,它同样会给出相同的分割点。如果不信服,可以自行验证。
以下是一些也可以使用的其他度量。
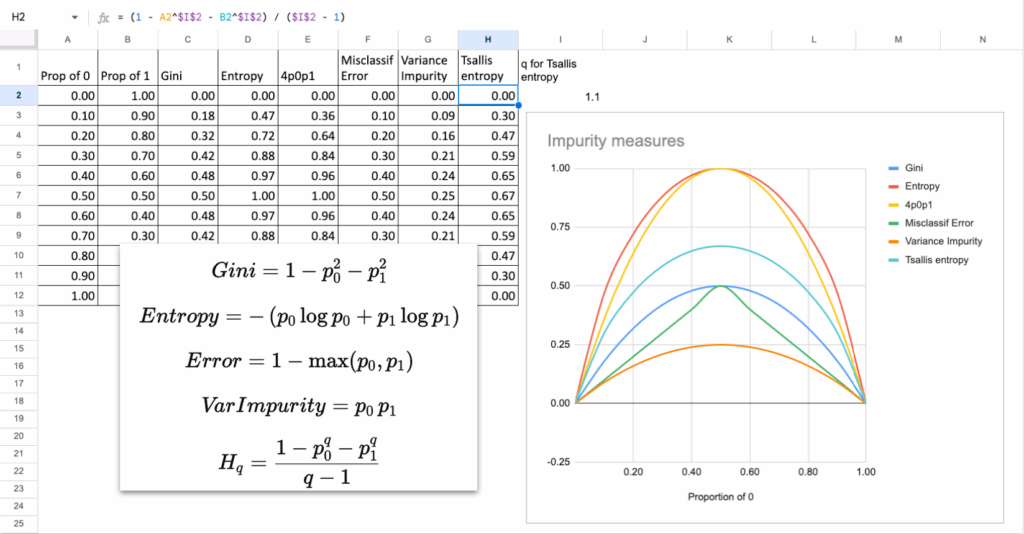
决策树分类器在Excel中的多种不纯度度量 – 图片由作者提供
Excel实战练习
使用其他参数和特征进行测试
构建第一个分割点后,可以扩展文件:
- 尝试使用信息熵代替基尼不纯度
- 尝试添加分类特征
- 尝试构建下一个分割点
- 尝试改变最大深度并观察欠拟合和过拟合
- 尝试为预测创建混淆矩阵
这些简单的测试已经足以帮助理解真实决策树的行为。
泰坦尼克号生存数据集的规则实现
一个自然的后续练习是为著名的泰坦尼克号生存数据集(CC0 / 公共领域)重新创建决策规则。
首先,可以仅从两个特征开始:性别和年龄。
在Excel中实现这些规则虽然冗长且有些繁琐,但这正是关键所在:它能让人真正理解决策规则的实际形态。
它们不过是一系列重复的IF / ELSE语句。
这就是决策树的本质:简单的规则,层层叠加。

Excel中针对泰坦尼克号生存数据集的决策树分类器实现(CC0 / 公共领域) – 图片由作者提供
结论
在Excel中实现决策树分类器出人意料地简单。
通过几个公式,就能揭示算法的核心:
- 列出可能的分割点
- 计算不纯度
- 选择最纯净的分割点

决策树分类器在Excel中的核心机制 – 图片由作者提供
这个简单的机制是更高级集成模型(如梯度提升树)的基础,本系列后续文章将对此进行讨论。







