曾有数据科学家认为岭回归是一个复杂的模型,因为其训练公式看起来更为复杂。
这正是“机器学习‘降临日历’”系列文章的目的之一——澄清这类复杂性。
本文将探讨线性回归的惩罚版本。
- 首先,将阐述为何需要正则化或惩罚,以及模型是如何被修改的。
- 其次,将探索不同类型的正则化及其效果。
- 接着,将演示如何使用正则化训练模型,并测试不同的超参数。
- 最后,会提出一个更深层次的问题:如何在惩罚项中对权重进行加权。
线性回归及其“条件”
当讨论线性回归时,常会提到一些应满足的条件。
可能听过类似的说法:
- 残差应服从高斯分布(有时会与目标变量需服从高斯分布混淆,后者是错误的)
- 解释变量之间不应存在共线性
在经典统计学中,这些条件是进行统计推断所必需的。在机器学习领域,重点在于预测,因此这些假设的重要性有所降低,但背后的潜在问题依然存在。
此处,将展示一个两个特征完全共线性的例子。
假设存在关系:y = x1 + x2,且 x1 = x2。
当然,如果它们完全相等,可以直接简化为 y=2*x1。但此处的核心观点是,即使特征高度相似,理论上仍可用它们构建模型,那么问题究竟何在?
当特征完全共线时,模型的解不唯一。下图展示了一个示例。
y = 10000x1 – 9998x2
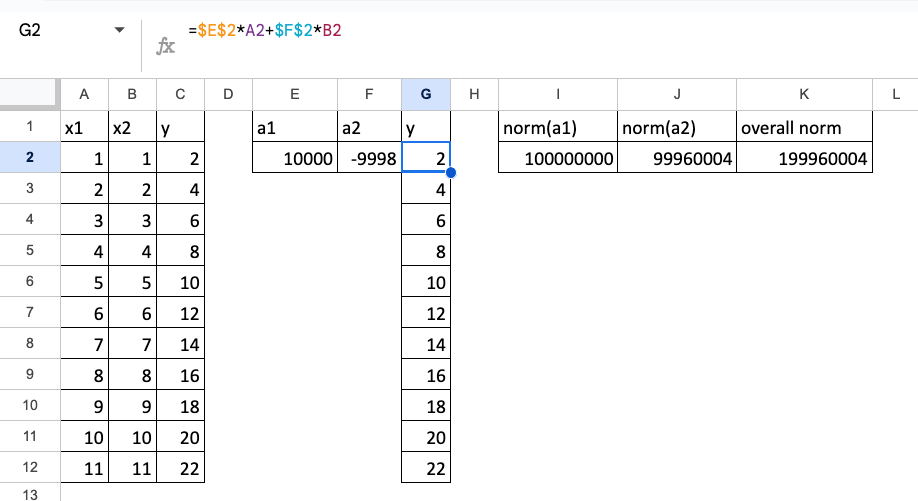
岭回归与Lasso在Excel中的实现 – 所有图片由作者提供
可以注意到,此时系数的范数非常大。
因此,正则化的核心思想就是限制系数的范数。
有趣的是,在应用正则化之后,模型的概念形式并未改变!
是的,线性回归的参数发生了变化,但模型的基本结构保持不变。
正则化的不同版本
其核心思想是将均方误差(MSE)与系数的范数结合起来。
目标不再仅仅是最小化MSE,而是最小化这两项之和。
使用哪种范数?可以是L1范数、L2范数,甚至是它们的组合。
有三种经典的正则化方法,对应着不同的模型名称。
岭回归(L2惩罚)
岭回归在损失函数中增加了对系数平方值的惩罚项。
直观理解:
- 大的系数会受到严重惩罚(因为平方运算)
- 系数被推向零
- 但永远不会精确等于零
效果:
- 所有特征都保留在模型中
- 系数更平滑、更稳定
- 对处理共线性非常有效
岭回归会收缩系数,但不进行特征选择。

Excel中的岭回归 – 所有图片由作者提供
Lasso回归(L1惩罚)
Lasso使用不同的惩罚项:系数的绝对值。
这一微小变化带来了重大影响。
使用Lasso时:
- 部分系数可以变为精确的零
- 模型会自动忽略某些特征
这正是LASSO名称的由来,它代表最小绝对收缩和选择算子。
- 算子:指添加到损失函数中的正则化算子
- 最小:源于最小二乘回归框架
- 绝对:使用系数的绝对值(L1范数)
- 收缩:将系数向零收缩
- 选择:可将某些系数设为零,实现特征选择
一个重要细微差别:
- 模型形式上仍具有相同数量的系数
- 但其中一部分在训练过程中被强制设为零
模型形式未变,但Lasso通过将系数驱动至零,有效地移除了特征。

Excel中的Lasso – 所有图片由作者提供
3. 弹性网络(L1 + L2)
弹性网络是岭回归和Lasso的结合。
它同时使用:
- L1惩罚项(类似Lasso)
- L2惩罚项(类似岭回归)
为何要结合?
因为:
- 当特征高度相关时,Lasso可能不稳定
- 岭回归能很好地处理共线性,但不进行特征选择
弹性网络在以下方面取得了平衡:
- 稳定性
- 收缩性
- 稀疏性
在实际数据集中,它通常是最实用的选择。
真正的变化:模型、训练与调优
从机器学习的角度审视这些差异。
模型并未真正改变
对于所有正则化版本,模型的表达式仍然是:
y = a x + b。
- 系数数量相同
- 预测公式相同
- 但系数的值会不同
从某种角度看,岭回归、Lasso和弹性网络并非不同的模型。
训练原理也相同
训练过程依然遵循:
- 定义损失函数
- 最小化损失函数
- 计算梯度
- 更新系数
唯一的区别在于:
- 损失函数现在包含了一个惩罚项
仅此而已。
增加了超参数(这是真正的区别)
对于标准线性回归,无法控制模型的“复杂度”。
- 标准线性回归:无超参数
- 岭回归:一个超参数(lambda)
- Lasso:一个超参数(lambda)
- 弹性网络:两个超参数
- 一个控制整体正则化强度
- 一个平衡L1与L2的比例
因此:
- 标准线性回归无需调优
- 惩罚回归则需要
这也是为什么标准线性回归常被视为“不完全是机器学习”,而正则化版本则显然是。
正则化梯度的实现
以普通最小二乘回归的梯度下降为参考,对于岭回归,只需为系数添加正则化项。
此处使用一个生成的数据集(与之前线性回归示例所用相同)。
可以看到三种“模型”在系数上存在差异。本章的目标是实现所有模型的梯度并进行比较。
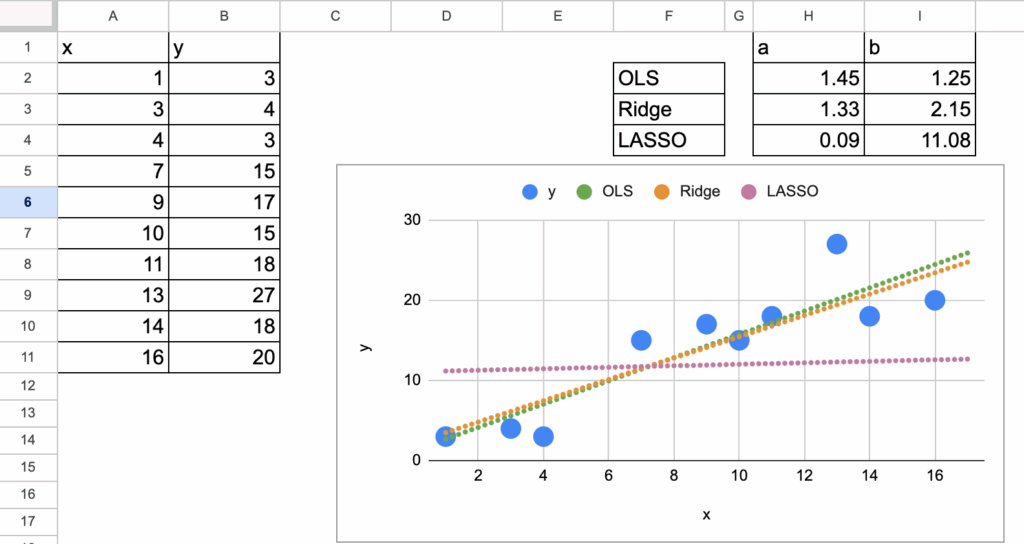
Excel中的岭回归与Lasso – 所有图片由作者提供
带惩罚梯度的岭回归
首先实现岭回归,只需修改系数a的梯度。
但这并不意味着截距b的值不变,因为b的梯度在每一步也依赖于a。
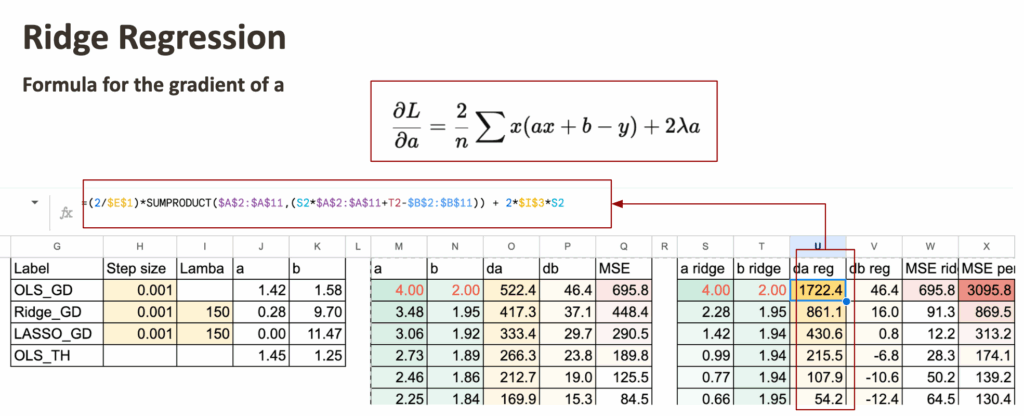
Excel中的岭回归与Lasso – 所有图片由作者提供
带惩罚梯度的LASSO
接着对LASSO进行类似操作。
唯一的区别同样在于系数a的梯度。
对于每个模型,还可以计算MSE和正则化后的MSE。观察它们在迭代过程中如何下降是相当令人满意的。
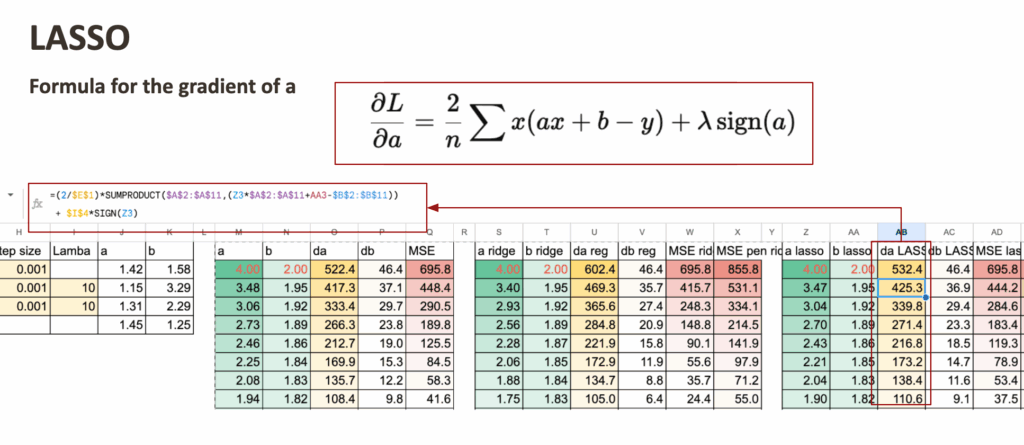
Excel中的岭回归与Lasso – 所有图片由作者提供
系数比较
现在,可以可视化三种模型的系数a。为了看清差异,输入了非常大的lambda值。
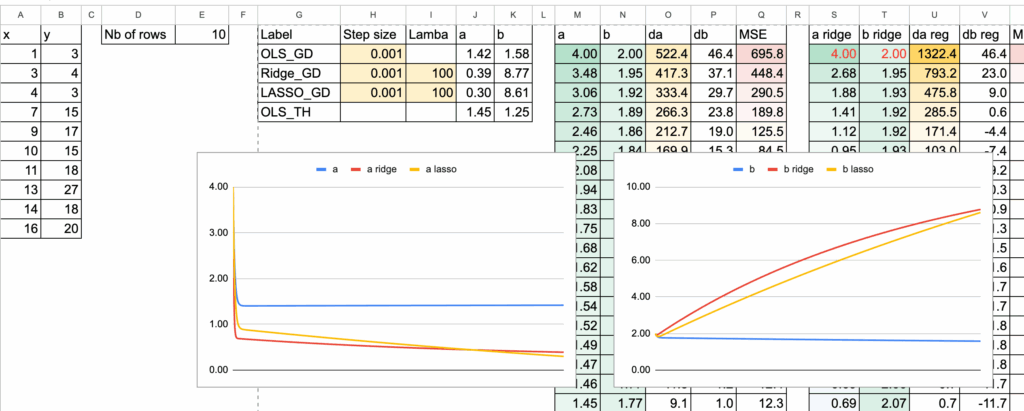
Excel中的岭回归与Lasso – 所有图片由作者提供
lambda的影响
对于较大的lambda值,系数a会变小。
如果LASSO的lambda值变得极大,理论上系数a将变为0。在数值计算中,需要改进梯度下降算法来实现这一点。
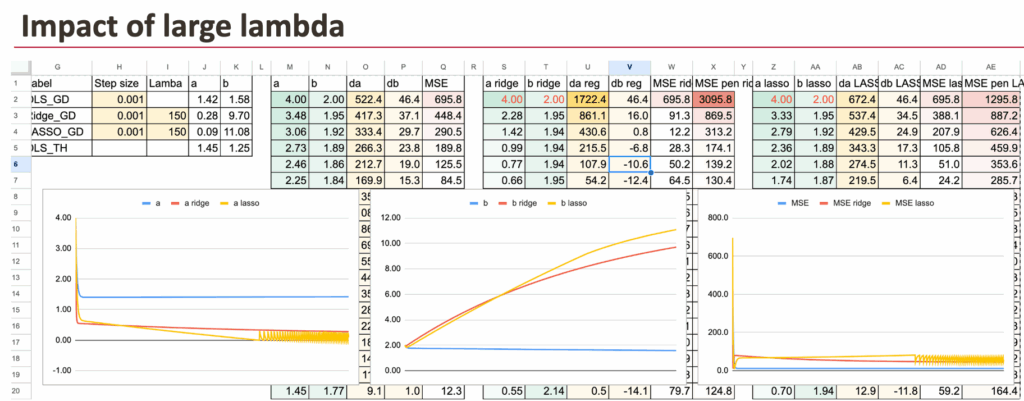
Excel中的岭回归与Lasso – 所有图片由作者提供
正则化逻辑回归?
在讨论逻辑回归时,一个自然的问题是:它是否也可以正则化?如果可以,它们叫什么?
答案当然是肯定的,逻辑回归同样可以正则化。
完全相同的思路适用。
逻辑回归也可以进行:
- L1惩罚
- L2惩罚
- 弹性网络惩罚
在常见用法中,没有像“岭逻辑回归”这样的特殊名称。
为什么?
因为这个概念已不再新颖。
在实践中,像scikit-learn这样的库通常只需指定:
- 损失函数
- 惩罚类型
- 正则化强度
命名的重要性在于概念刚被提出时。
如今,正则化已成为一个标准选项。
其他可以探讨的问题包括:
- 正则化总是有用的吗?
- 特征缩放如何影响正则化线性回归的性能?







