支持向量机(SVM)这一模型,最初正是激发人们使用Excel来深入理解机器学习的动力。
今天,将看到一个与通常几何视角不同的SVM解释。常见的解释往往从间隔分离器、到超平面的距离、几何构造等概念开始。而本文将采取另一种方式:从已知的知识出发,逐步构建模型。
或许今天,你终于能恍然大悟:“哦,现在我更明白了。”
在已知基础上构建新模型
一个核心的学习原则很简单:始终从已知出发。
在学习SVM之前,通常已经掌握了逻辑回归、惩罚与正则化等模型和概念。今天的目标不是引入一个全新的模型,而是对现有模型进行转化。
训练数据集与标签约定
为了清晰地解释SVM,将使用一个单特征数据集。这可能是首次看到仅用一个特征来解释SVM。为什么这么做?
对于线性回归或逻辑回归,通常从单特征开始。SVM也应如此,以便在不同模型间进行恰当的对比。如果一个模型无法用单一特征解释,那么对其工作原理的理解可能并不透彻。使用单特征使模型更易于实现、可视化和调试。
为此,生成了两个数据集,用以说明线性分类器可能面临的两种典型情况:一个是完全可分的,另一个则不是完全可分的。
此外,标签约定使用-1和1,而非0和1。这背后有有趣的历史原因,涉及到广义线性模型与机器学习视角的差异。
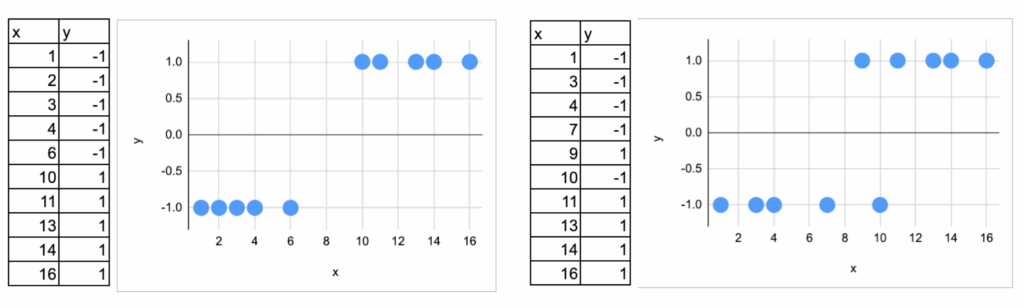
在逻辑回归中,应用Sigmoid函数之前,会计算一个线性得分,即对数几率。这个量可以取任何实数值。
- 正值对应一个类别,
- 负值对应另一个类别,
- 零则是决策边界。
使用标签-1和1自然地契合了这种解释,它强调了线性得分的符号,而无需经过概率转换。因此,这里处理的是一个纯粹的线性模型,而非广义线性模型框架下的模型。没有Sigmoid函数,没有概率,只有一个线性决策得分。
一个简洁的表达方式是考察量:y(ax + b) = y f(x)。
- 若该值为正,则点被正确分类。
- 若该值很大,则分类置信度高。
- 若该值为负,则点被错误分类。
至此,讨论的还不是SVM,只是在明确线性设定下“良好分类”的含义。
从对数损失到新的损失函数
基于此约定,可以将逻辑回归的对数损失直接写为y f(x) = y (ax+b)的函数,并绘制其图像。
现在,引入一个新的损失函数,称为合页损失。将两种损失绘制在同一图表上,可以看到它们的形状非常相似。这类似于决策树分类器中基尼不纯度与熵的比较。
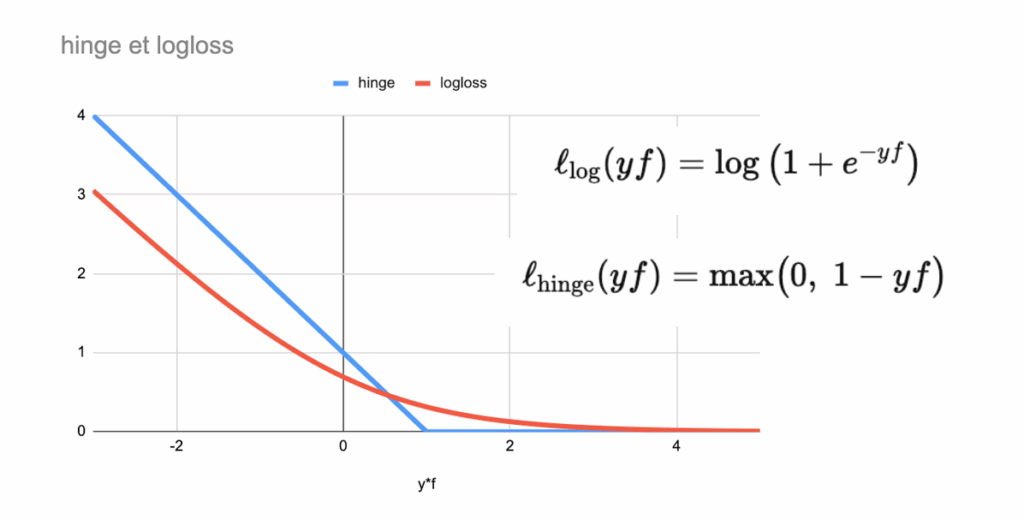
两种损失的核心思想都是惩罚:
- 被错误分类的点(yf(x) < 0),
- 以及距离决策边界太近的点。
区别在于如何施加惩罚。
- 对数损失以平滑渐进的方式惩罚错误,即使分类正确的点也会受到轻微惩罚。
- 合页损失则更加直接和突兀。一旦一个点被正确分类且具有足够的间隔,它就不再受到任何惩罚。
因此,目标不是改变对分类好坏的定义,而是简化惩罚的方式。
一个自然的问题是:能否使用平方损失?毕竟线性回归也可用作分类器。但这样做会立即发现问题:平方损失会持续惩罚那些已经分类得很好的点。模型不再专注于决策边界,而是试图拟合精确的数值目标。这就是线性回归通常分类效果不佳的原因,也说明了损失函数选择的重要性。
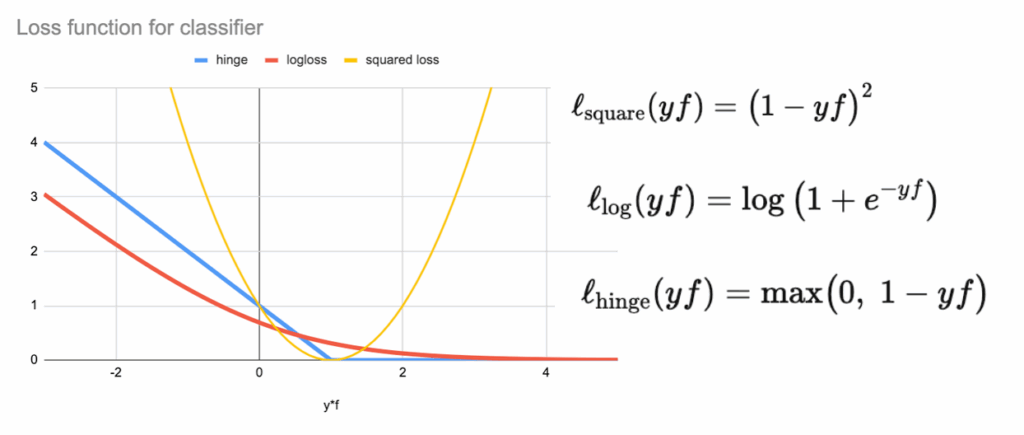
新模型的描述
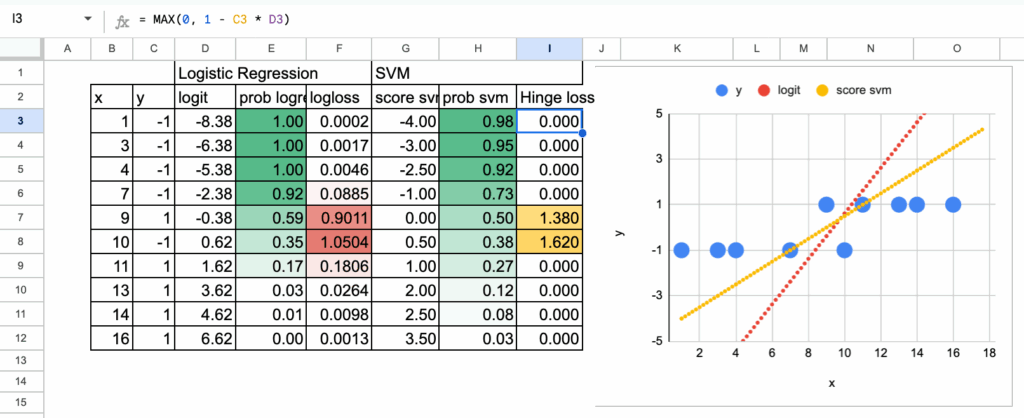
现在假设模型已经训练完成,直接观察结果。
对于两种模型,计算完全相同的量:
- 线性得分(在逻辑回归中称为对数几率),
- 概率(在两种情况下都可应用Sigmoid函数),
- 以及损失值。
这使得可以对两种方法进行逐点的直接比较。尽管损失函数不同,但线性得分和最终的分类结果在这个数据集上非常相似。
对于完全可分的数据集,结果是直接的:所有点都被正确分类且距离决策边界足够远。因此,每个观测值的合页损失都为零。
这引出了一个重要结论:当数据完全可分时,解并不唯一。事实上,存在无限多个线性决策函数能达到完全相同的结果。可以平移直线、轻微旋转或缩放系数,而分类结果依然完美,损失处处为零。
那么接下来做什么?引入正则化。
正如在岭回归中一样,添加一个对系数大小的惩罚项。这个附加项不会提高分类准确率,但它允许从所有可能的解中选择一个。在数据集中,最终得到的是斜率a最小的那个解。

至此,SVM模型已经构建完成。
现在可以写出逻辑回归和SVM两个模型的成本函数。逻辑回归也可以正则化,它仍然被称为逻辑回归。
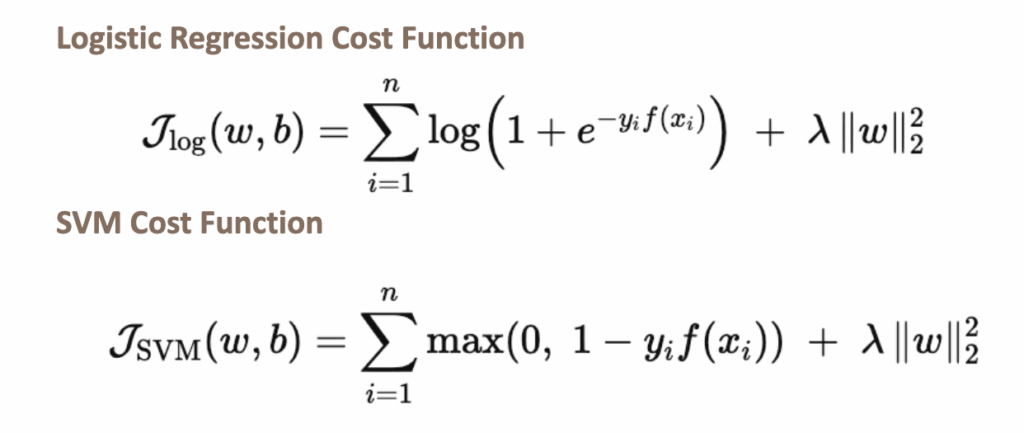
那么,为什么模型名称中包含“支持向量”?
观察数据集,会发现只有少数点(例如值为6和10的点)足以确定决策边界。这些点被称为支持向量。在目前使用的视角下,无法直接识别它们。后续会看到,另一种视角会使它们自然显现。
对于另一个不可分数据集,可以进行同样的练习,原理完全相同。但现在可以看到,对于某些点,合页损失不为零。在下面的案例中,可以直观地看到需要四个点作为支持向量。
使用梯度下降训练SVM模型
现在使用梯度下降显式地训练SVM模型。这里没有引入新内容,只是复用了已在线性和逻辑回归中应用过的优化逻辑。
新约定:Lambda (λ) 或 C
在之前研究的许多模型(如岭回归或逻辑回归)中,目标函数写作:数据拟合损失 + λ ∥w∥。其中,正则化参数λ控制对系数大小的惩罚。
对于SVM,通常的约定略有不同,使用C放在数据拟合项前面。
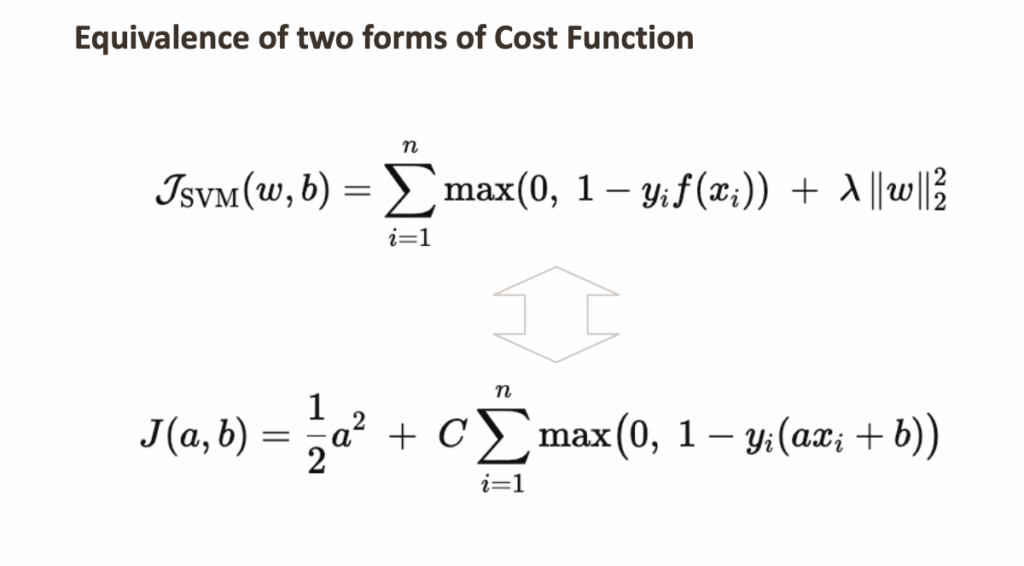
两种表述是等价的,仅在于目标函数的缩放不同。保留参数C是因为它是SVM中的标准符号。
梯度(次梯度)
使用线性决策函数,可以为每个点定义间隔:mi = yi (axi + b)。只有满足 mi < 1 的观测点才对合页损失有贡献。
目标函数的次梯度如下所示,可以在Excel中使用逻辑掩码和SUMPRODUCT函数实现。
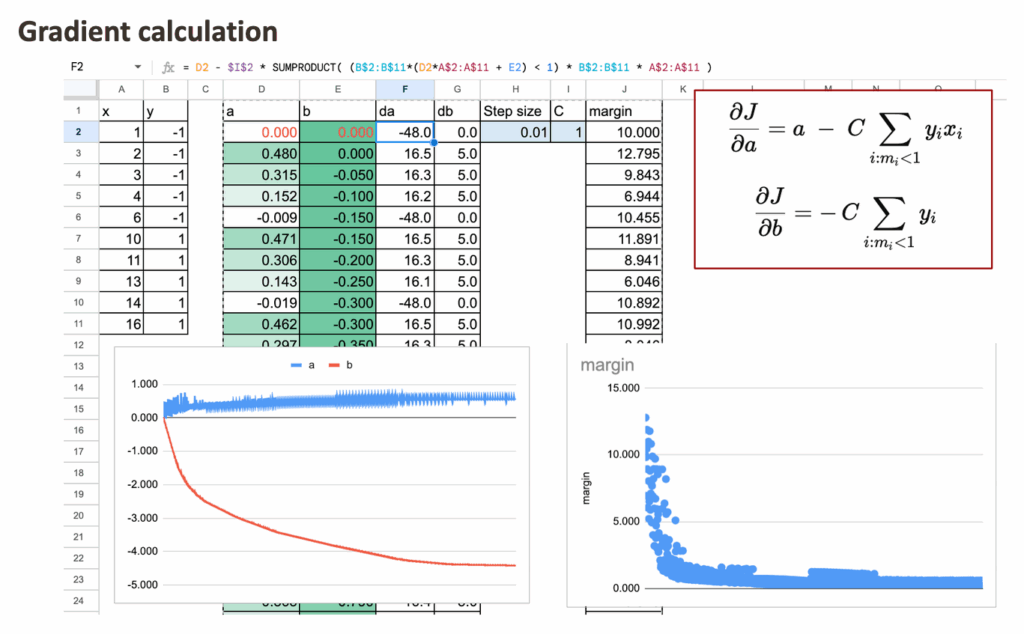
参数更新
给定学习率或步长η,梯度下降更新公式如下,可以采用通常的公式进行计算。
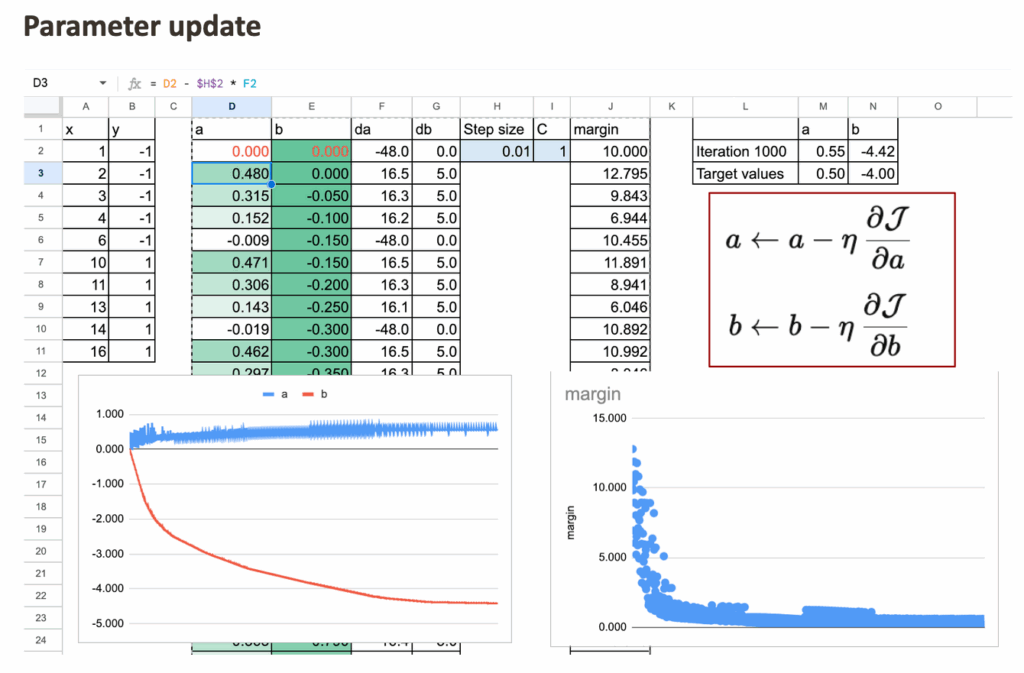
迭代这些更新直到收敛。顺便提一下,这个训练过程还提供了一个很好的可视化效果。在每次迭代中,随着系数更新,间隔的大小会发生变化。因此可以逐步可视化间隔在学习过程中的演变。
SVM的优化视角与几何视角
下图展示了SVM模型目标函数用两种不同语言表达的同一概念。

左侧,模型被表达为一个优化问题。最小化两项的组合:一项通过惩罚大系数来保持模型简单,另一项则惩罚分类错误或间隔违反。这是目前一直使用的视角,在考虑损失函数、正则化和梯度下降时很自然,是实现和优化的最便捷形式。
右侧,同一个模型以几何方式表达。不再谈论损失,而是谈论间隔、约束以及到分离边界的距离。当数据完全可分时,模型寻找具有最大可能间隔的分离线,不允许任何违反。这是硬间隔情况。当完美分离不可能时,允许违反,但会受到惩罚,这导致了软间隔情况。
重要的是理解这两种视角是严格等价的。优化公式自动强制执行几何约束:惩罚大系数对应于最大化间隔,惩罚合页违反对应于允许但控制间隔违反。因此,这不是两个不同的模型或两个不同的想法,而是同一个SVM的两个互补视角。
一旦明确了这种等价性,SVM就变得不那么神秘了:它只是一个具有特定误差衡量和复杂度控制方式的线性模型,这自然引出了众所周知的最大间隔解释。
统一的线性分类器
从优化视角出发,现在可以退一步,看到更大的图景。
所构建的不仅仅是“SVM”,而是一个通用的线性分类框架。一个线性分类器由三个独立的选择定义:一个线性决策函数、一个损失函数和一个正则化项。
一旦明确了这一点,许多模型就表现为这些元素的简单组合。在实践中,这正是scikit-learn中SGDClassifier所能做到的。
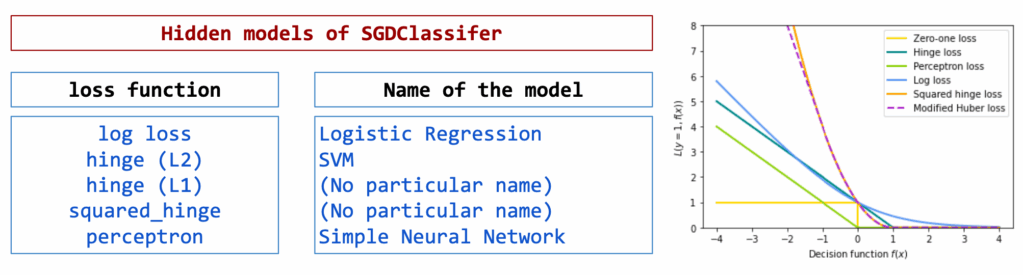
从同一视角出发,可以:
- 将合页损失与L1正则化结合,
- 用平方合页损失替换合页损失,
- 使用对数损失、合页损失或其他基于间隔的损失,
- 根据期望的行为选择L2或L1惩罚。
每种选择都会改变惩罚错误的方式或控制系数的方式,但底层模型保持不变:一个通过优化训练的线性决策函数。
原始形式与对偶形式
你可能已经听说过SVM的对偶形式。到目前为止,一直在原始形式下工作:直接优化模型系数,使用损失函数和正则化。
对偶形式是表述同一优化问题的另一种方式。它不是为特征分配权重,而是为每个数据点分配一个系数,通常称为alpha。
不会在Excel中推导或实现对偶形式,但可以观察其结果。使用scikit-learn可以计算alpha值,并验证:原始形式和对偶形式导向相同的模型、相同的决策边界和相同的预测。
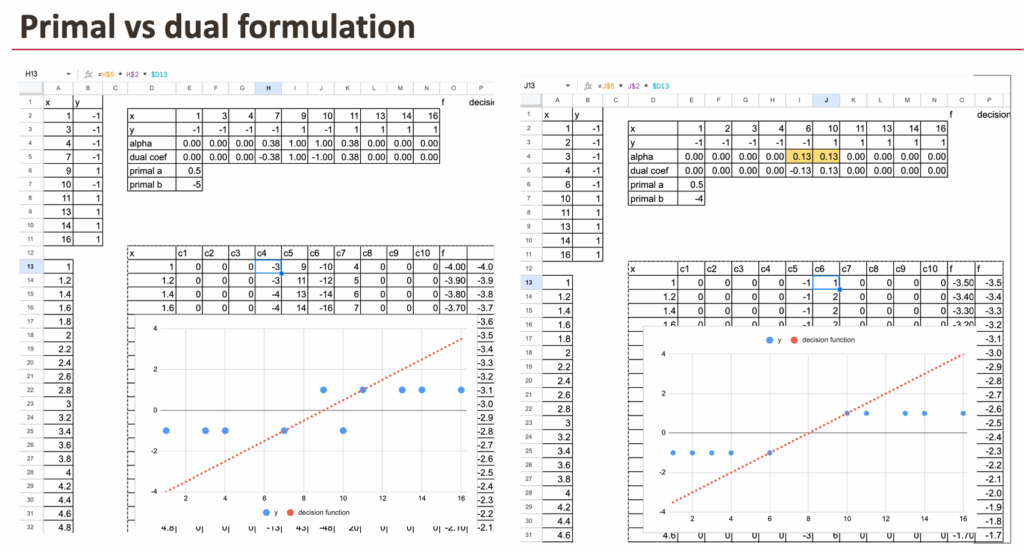
对偶形式对SVM特别有趣的地方在于:
- 大多数alpha值恰好为零,
- 只有少数数据点具有非零的alpha。
这些点就是支持向量。这种行为是合页损失等基于间隔的损失所特有的。
最后,对偶形式也解释了为什么SVM可以使用核技巧。通过处理数据点之间的相似性,可以在不改变优化框架的情况下构建非线性分类器。
结论
本文没有将SVM作为一个带有复杂公式的几何对象来介绍,而是从已知的模型出发,逐步构建了它。
通过仅改变损失函数,然后添加正则化,自然地得出了SVM。模型本身没有改变,改变的只是惩罚错误的方式。
从这个角度看,SVM并非一个新的模型家族。它是线性和逻辑回归的自然延伸,只是通过不同的损失函数视角来看待。
本文还展示了:
- 优化视角和几何视角是等价的,
- 最大间隔解释直接来源于正则化,
- 支持向量的概念从对偶视角中自然浮现。
一旦这些联系变得清晰,SVM就变得更容易理解,也更容易在其他线性分类器中找到其位置。






