在过去的18篇文章中,已经探讨了机器学习中大多数核心模型,它们主要分为三大类:基于距离和密度的模型、基于树或规则的模型,以及基于权重的模型。
此前,每篇文章都聚焦于单个模型的独立训练。集成学习则彻底改变了这一视角。它并非一个独立的模型,而是一种组合这些基础模型以构建新模型的方法。
如下图所示,集成模型是一种元模型。它位于各个独立模型之上,并对它们的预测结果进行汇总。
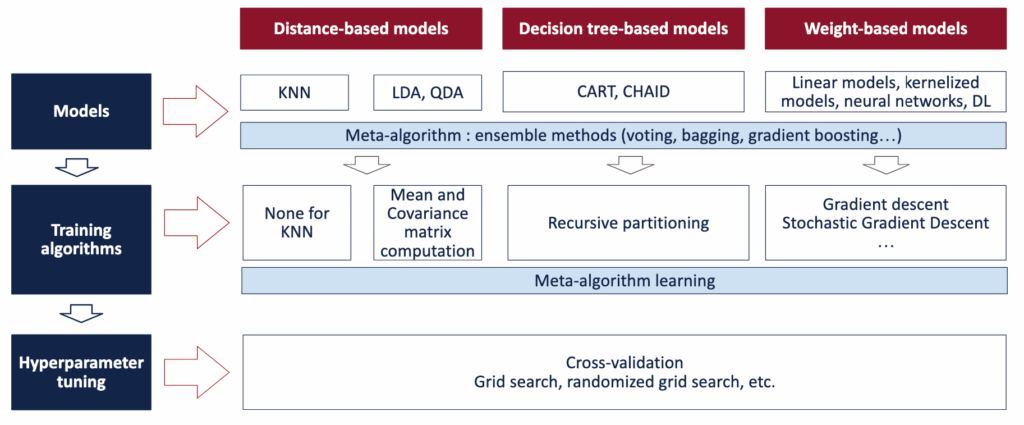
机器学习中的三个学习步骤 – 图片由作者提供
投票法:最简单的集成思想
集成学习最简单的形式是投票法。
其思路几乎不言自明:训练多个模型,获取它们的预测结果,然后计算平均值。如果一个模型在一个方向上出错,而另一个模型在相反方向上出错,那么误差应该会相互抵消。至少,直觉上是这样。
理论上,这听起来合理。但在实践中,情况却大不相同。
一旦尝试对真实模型进行投票,一个事实就会变得显而易见:投票法并非魔法。简单地平均预测结果并不能保证性能更好。在许多情况下,它实际上会使情况变得更糟。
原因很简单。当组合行为差异很大的模型时,它们的弱点也会被组合起来。如果模型产生的错误不具有互补性,那么求平均可能会稀释有用的结构,而不是强化它。
为了清晰地理解这一点,可以考虑一个非常简单的例子。使用同一个数据集训练一个决策树和一个线性回归模型。决策树捕捉局部的、非线性的模式。线性回归捕捉全局的线性趋势。当平均它们的预测时,并不会得到一个更好的模型。得到的是一个折衷的结果,通常比每个模型单独使用时更差。
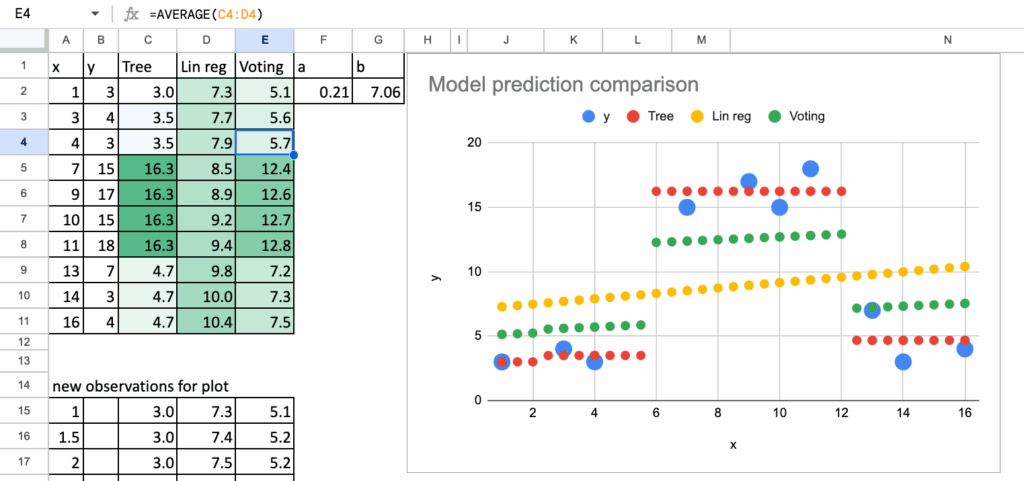
投票法机器学习 – 所有图片由作者提供
这阐明了一个重要观点:集成学习需要的不仅仅是求平均。它需要一种策略,一种能够真正提高稳定性或泛化能力的模型组合方式。
此外,如果将集成模型视为一个单一模型,那么它也必须像模型一样被训练。简单的平均法没有可调整的参数,没有需要学习或优化的内容。
对投票法一个可能的改进是为模型分配不同的权重。可以尝试学习哪些模型应该更重要,而不是给每个模型相同的重要性。但一旦引入权重,新的问题就会出现:如何训练这些权重?此时,集成模型本身就成了一个需要拟合的模型。
这一观察自然引向了更具结构性的集成方法。
本文将从一种统计方法开始,即在求平均之前对训练数据集进行重采样:Bagging。
Bagging背后的直觉
为什么叫“Bagging”?
什么是Bagging?
答案其实隐藏在名字本身。
Bagging = Bootstrap + Aggregating(自助采样 + 聚合)。
可以立刻看出,这很可能是数学家或统计学家的命名。 
在这个略显令人生畏的词汇背后,其思想却极其简单。Bagging就是做两件事:首先,使用自助法创建数据集的多个版本;其次,聚合从这些数据集获得的结果。
因此,其核心思想不在于改变模型,而在于改变数据。
对数据集进行自助采样
自助采样意味着有放回地对数据集进行抽样。每个自助样本的大小与原数据集相同,但观测值不同。有些行会出现多次,有些行则会消失。
在Excel中,这非常容易实现,更重要的是,非常直观可见。
首先为数据集添加一个ID列,为每一行分配一个唯一标识符。然后,使用RANDBETWEEN函数随机抽取行索引。每次抽取对应自助样本中的一行。通过重复这个过程,可以生成一个看起来熟悉但与原始数据集略有不同的完整数据集。
仅这一步就已经使Bagging的概念变得具体。可以直观地看到重复项,可以看到哪些观测值缺失。没有任何抽象之处。
下方可以看到从同一原始数据集生成的自助样本示例。每个样本讲述的故事都略有不同,尽管它们都来自相同的数据。
这些替代数据集是Bagging的基础。
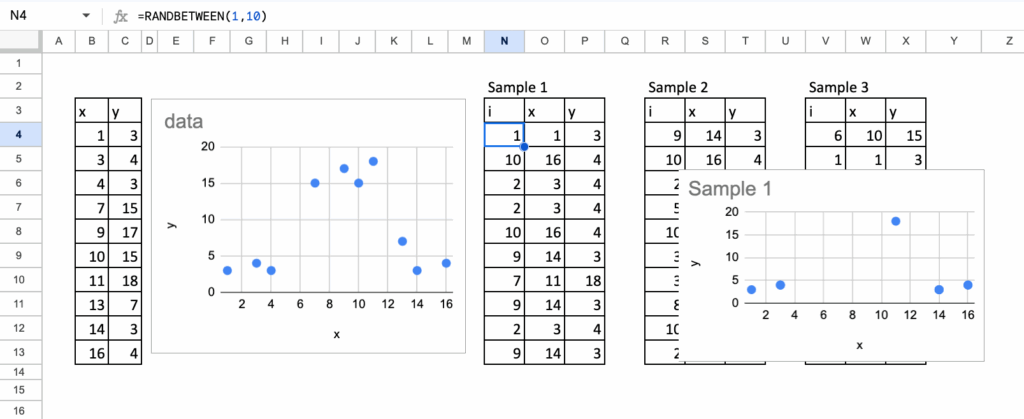
作者生成的数据集 – 图片由作者提供
Bagging线性回归:理解原理
Bagging流程
是的,这很可能是第一次听说对线性回归进行Bagging。
理论上,这没有任何问题。如前所述,Bagging是一种可以应用于任何基础模型的集成方法。线性回归是一个模型,因此从技术上讲,它符合条件。
然而,在实践中,很快就会发现这并不十分有用。
但没有什么能阻止我们这样做。恰恰因为它不太有用,所以成为了一个绝佳的学习示例。因此,让我们尝试一下。
对于每个自助样本,都拟合一个线性回归。在Excel中,这很简单。可以直接使用LINEST函数来估计系数。图中每种颜色对应一个自助样本及其相关的回归线。
到目前为止,一切行为都符合预期。这些线条彼此接近,但并不完全相同。每个自助样本都会轻微改变系数,从而改变拟合线。
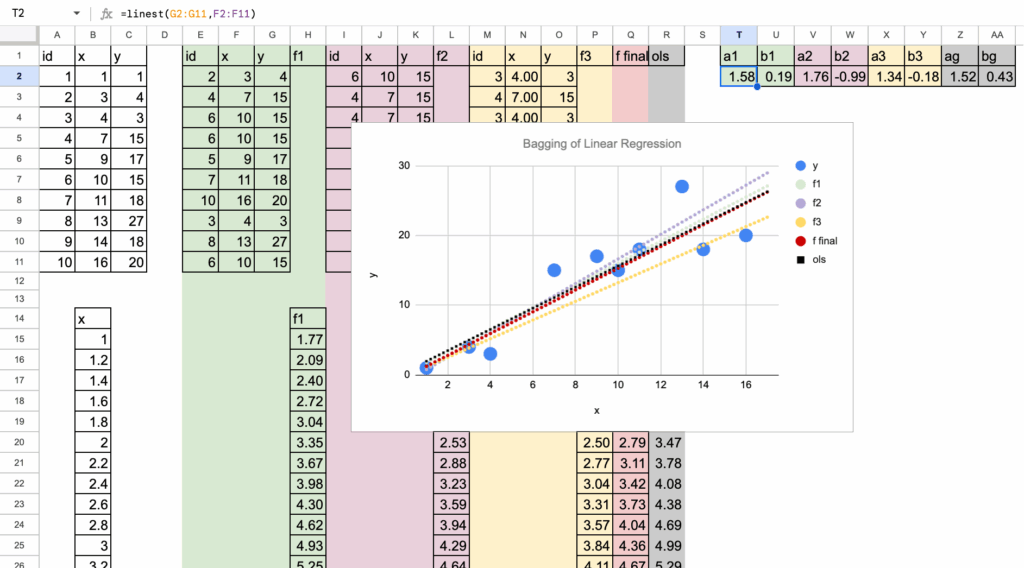
线性回归的Bagging – 图片由作者提供
现在到了关键的观察点。
可能会注意到图中用黑色绘制了一个额外的模型。这个模型对应的是在原始数据集上拟合的标准线性回归,没有进行自助采样。
当将其与经过Bagging的模型进行比较时,会发生什么?
当平均所有这些线性回归的预测时,最终结果仍然是一个线性回归。预测的形状没有改变。变量之间的关系仍然是线性的。并没有创建一个表达能力更强的模型。
更重要的是,经过Bagging的模型最终与在原始数据上训练的标准线性回归非常接近。
甚至可以进一步推进这个例子,使用一个具有明显非线性结构的数据集。在这种情况下,每个在自助样本上拟合的线性回归都会以自己的方式挣扎。根据样本中哪些观测值被重复或缺失,有些线会略微向上倾斜,有些则会向下倾斜。
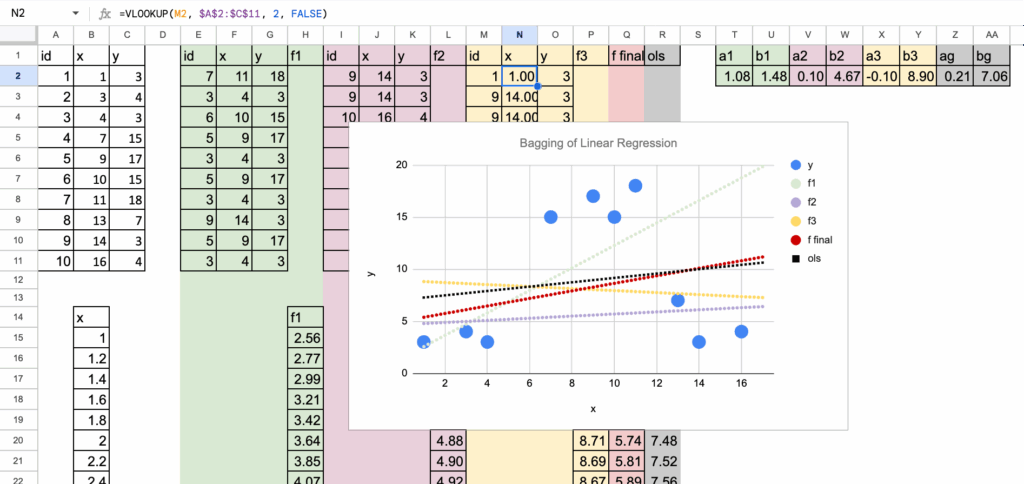
线性回归的Bagging – 图片由作者提供
自助法置信区间
从预测性能的角度来看,对线性回归进行Bagging并不十分有用。
然而,自助法对于一个重要的统计概念仍然极其有用:估计预测的置信区间。
可以不仅仅看平均预测,而是查看所有自助模型产生的预测分布。对于每个输入值,现在都有许多预测值,每个自助样本产生一个。
量化不确定性的一种简单直观的方法是计算这些预测值的标准差。这个标准差告诉我们预测对数据变化的敏感程度。数值小意味着预测稳定。数值大意味着预测不确定。
这个想法在Excel中很自然地实现。一旦获得了所有自助模型的预测,计算它们的标准差就很简单。结果可以解释为预测周围的置信带。
这在下面的图中清晰可见。解释很直接:在训练数据稀疏或高度分散的区域,置信区间变宽,因为不同自助样本的预测差异很大。
相反,在数据密集的区域,预测更加稳定,置信区间变窄。
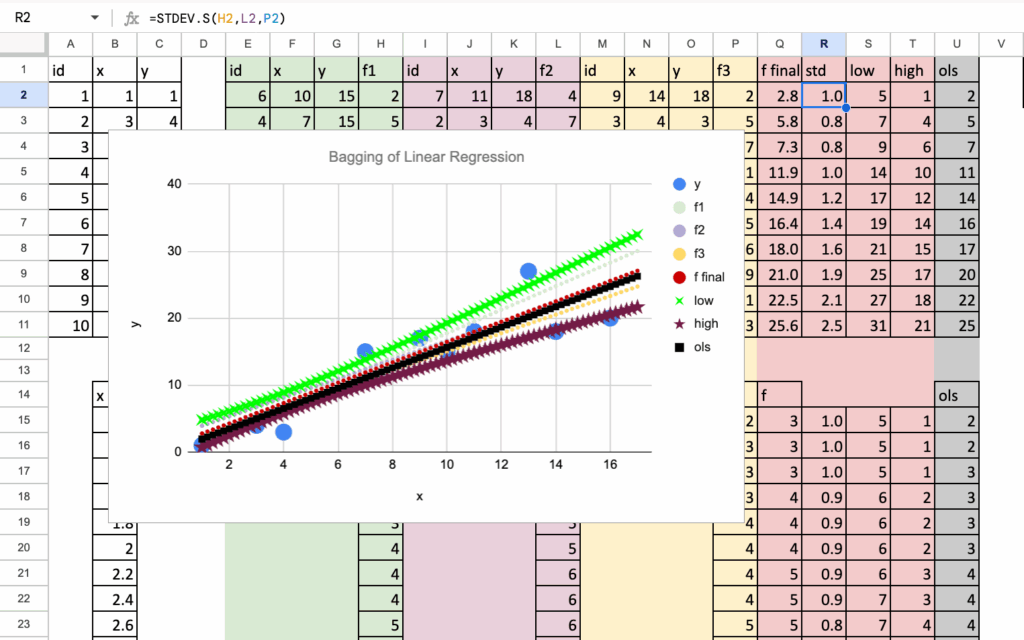
现在,当将其应用于非线性数据时,一些情况变得非常清晰。在线性模型难以拟合数据的区域,不同自助样本的预测结果分散得多。置信区间变得更宽。
这是一个重要的见解。即使Bagging没有提高预测准确性,它也提供了关于不确定性的宝贵信息。它告诉我们模型在哪些地方可靠,在哪些地方不可靠。
在Excel中直接看到这些置信区间从自助样本中产生,使得这个统计概念非常具体和直观。

Bagging决策树:从弱学习器到强模型
现在转向决策树。
Bagging的原理完全保持不变。生成多个自助样本,在每个样本上训练一个模型,然后聚合它们的预测。
改进了Excel实现,使分割过程更加自动化。为了在Excel中保持可管理性,将树限制为单次分割。构建更深的树是可能的,但在电子表格中很快就会变得繁琐。
下方可以看到两棵经过自助采样的树。总共通过简单地复制和粘贴公式构建了八棵,这使得过程直接且易于复现。
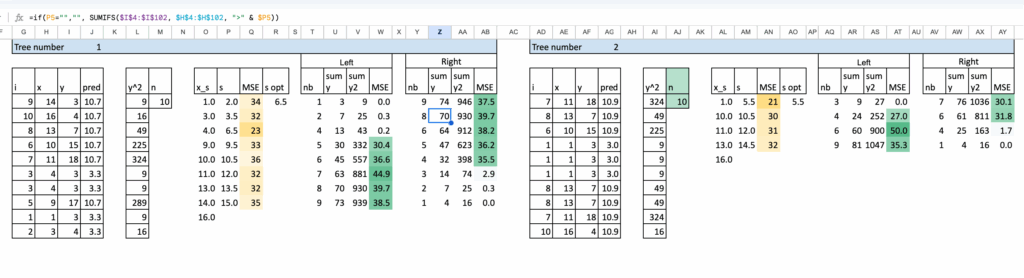
由于决策树是高度非线性的模型,其预测结果是分段常数,因此对它们的输出求平均具有平滑效果。
因此,Bagging自然地平滑了预测。聚合后的模型产生更渐进的过渡,而不是单个树产生的尖锐跳跃。
在Excel中,这种效果很容易观察到。经过Bagging的预测明显比任何单棵树的预测更平滑。
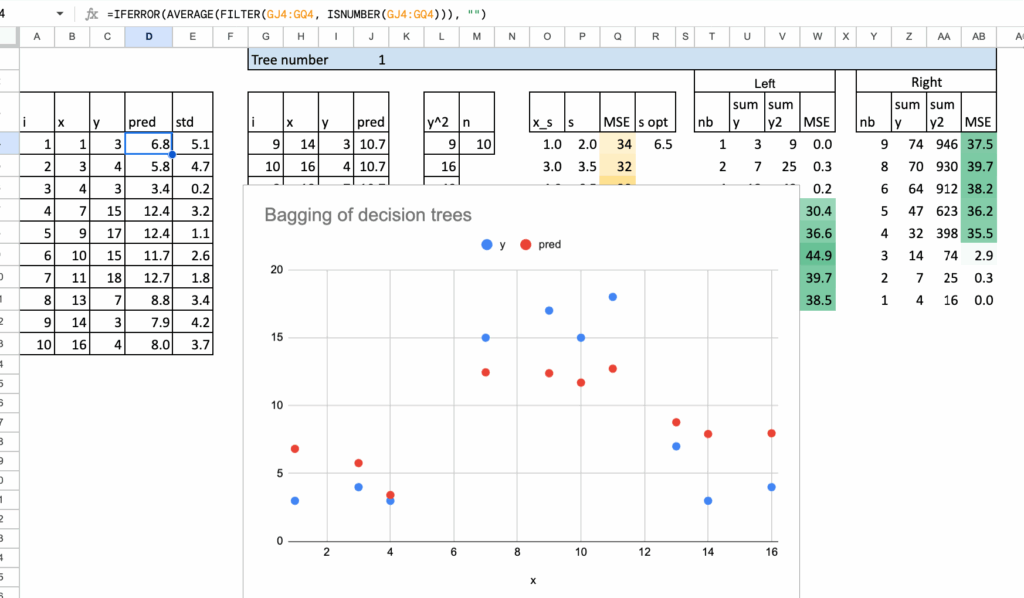
有些人可能已经听说过决策树桩,即最大深度为一的决策树。这正是这里使用的模型。每个模型都极其简单。就其本身而言,树桩是一个弱学习器。
这里的问题是:
当与Bagging结合时,一组决策树桩是否足够?
后续的机器学习“Advent Calendar”系列文章中将回到这个问题。
随机森林:扩展Bagging
那么随机森林呢?
这很可能是数据科学家最喜欢的模型之一。
那么,为什么不在这里讨论它,即使在Excel中?
事实上,刚刚构建的内容已经非常接近随机森林了!
要理解原因,请回顾随机森林引入了两种随机性来源。
- 第一种是数据集的自助采样。这正是Bagging已经完成的工作。
- 第二种是分割过程中的随机性。在每次分割时,只考虑特征的随机子集。
然而,在这个例子中,只有一个特征。这意味着没有可供选择的内容。特征随机性根本不适用。
因此,这里得到的结果可以看作是一个简化的随机森林。
一旦这个概念清晰,将想法扩展到多个特征就只是增加了一层随机性,而不是一个新概念。
甚至可能会问,可以将这个原理应用于线性回归,构建一个随机…
结论
集成学习与其说是关于复杂模型,不如说是关于管理不稳定性。
简单的投票法很少有效。对线性回归进行Bagging改变不大,主要具有教学意义,尽管它对估计不确定性有用。然而,对于决策树,Bagging真正重要:对不稳定的模型进行平均可以得到更平滑、更稳健的预测。
随机森林自然地扩展了这一思想,增加了额外的随机性,而没有改变核心原则。在Excel中观察,集成方法不再是黑盒,而成为逻辑上的下一步。
延伸阅读
感谢对机器学习“Advent Calendar”系列的支持。
人们通常谈论很多监督学习,但无监督学习有时被忽视,尽管它可以揭示任何标签都无法显示的结构。
如果想进一步探索这些想法,以下三篇文章深入探讨了强大的无监督模型。
k-means的改进版和更灵活的版本。
与k-means不同,GMM允许簇拉伸、旋转并适应数据的真实形状。
但k-means和GMM何时会产生不同的结果?
请查看这篇文章以了解具体示例和视觉比较。
一种巧妙的方法,通过比较每个点的局部密度与其邻居来检测异常。
所有Excel文件均可通过此Kofi链接获取。支持对作者意义重大。价格将在本月内上涨,因此早期支持者将获得最佳价值。