午夜悖论
设想这样一个场景:正在构建一个用于预测电力需求或出租车订单量的模型。于是,将时间(例如分钟数)从午夜开始作为特征输入模型。这看起来清晰简单,对吗?
现在,模型看到了23:59(一天中的第1439分钟)和00:01(一天中的第1分钟)。对人类而言,这两者仅相隔两分钟。但对于模型来说,它们却相距甚远。这就是“午夜悖论”。是的,模型很可能处于“时间失明”状态。
为何会出现这种情况?
因为大多数机器学习模型将数字视为直线,而非循环的圆。
线性回归、K近邻、支持向量机甚至神经网络都会以线性逻辑处理数字,认为较大的数字“多于”较小的数字。它们无法理解时间是循环往复的。午夜成为了模型无法处理的边界情况。
如果在模型中加入小时信息后效果不佳,并且模型在日期边界附近表现挣扎,这很可能就是原因所在。
标准编码方法的失效
接下来探讨几种常见的处理方法,其中至少有一种可能被使用过。
- 整数编码法
将小时编码为0到23的数字。这种方法在23点和0点之间制造了一个人为的“悬崖”。因此,模型会认为午夜是一天中变化最大的时刻。然而,午夜与晚上11点的差异,真的比晚上10点与9点的差异更大吗?
当然不是。但模型对此一无所知。
下图展示了小时在“线性”模式下的表示。
# 生成数据
date_today = pd.to_datetime('today').normalize()
datetime_24_hours = pd.date_range(start=date_today, periods=24, freq='h')
df = pd.DataFrame({'dt': datetime_24_hours})
df['hour'] = df['dt'].dt.hour
# 计算正弦和余弦
df["hour_sin"] = np.sin(2 * np.pi * df["hour"] / 24)
df["hour_cos"] = np.cos(2 * np.pi * df["hour"] / 24)
# 绘制线性模式下的小时
plt.figure(figsize=(15, 5))
plt.plot(df['hour'], [1]*24, linewidth=3)
plt.title('线性模式下的小时表示')
plt.xlabel('小时')
plt.xticks(np.arange(0, 24, 1))
plt.ylabel('值')
plt.show()
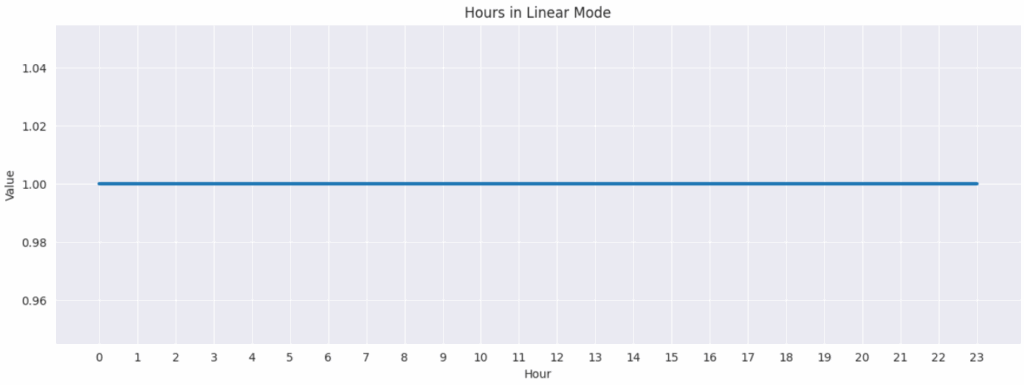
线性模式下的小时表示。作者供图。
- 独热编码法
如果对小时进行独热编码呢?创建24个二进制列。问题解决了吗?某种程度上是的。这种方法修复了人为的间隔,但丢失了邻近性。凌晨2点不再比晚上10点更接近凌晨3点。
同时,维度也急剧膨胀。对于树模型而言,这令人烦恼。对于线性模型,则可能效率低下。
因此,需要寻找一种可行的替代方案。
- 解决方案:三角映射
关键在于思维模式的转变:
停止将时间视为一条直线,而应将其视为一个圆。
24小时制的一天是循环往复的。因此,编码方式也应循环起来,以圆形思维处理。每个小时都是圆环上均匀分布的一个点。要表示圆上的一个点,不能仅用一个数字,而需要使用两个坐标:x 和 y。
这正是正弦和余弦函数的用武之地。
背后的几何原理
圆上的每个角度都可以通过正弦和余弦映射到一个唯一的点。这为模型提供了平滑、连续的时间表示。
plt.figure(figsize=(5, 5))
plt.scatter(df['hour_sin'], df['hour_cos'], linewidth=3)
plt.title('循环模式下的小时表示')
plt.xlabel('小时')
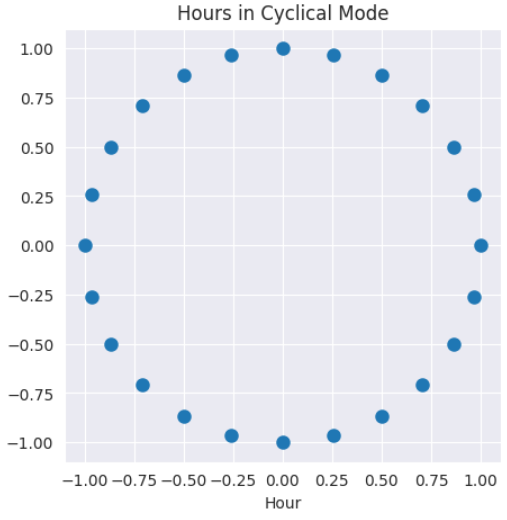
经过正弦和余弦变换后的小时循环模式。作者供图。
以下是计算一天中小时周期的数学公式:

- 首先,
2 * π * hour / 24将每个小时转换为一个角度。午夜和晚上11点最终在圆上几乎处于相同位置。 - 然后,正弦和余弦将该角度投影到两个坐标上。
- 这两个值共同唯一地定义了该小时。现在,23:00和00:00在特征空间中变得接近。这正是期望达到的效果。
同样的思路适用于分钟、星期几或一年中的月份。
代码实践
以家用电器能耗预测数据集 [4] 为例进行实验。尝试使用随机森林回归模型(一种树模型)来改进预测效果。
Candanedo, L. (2017). Appliances Energy Prediction [Dataset]. UCI Machine Learning Repository. https://doi.org/10.24432/C5VC8G. Creative Commons 4.0 License.
# 导入库
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
from ucimlrepo import fetch_ucirepo
获取数据。
# 获取数据集
appliances_energy_prediction = fetch_ucirepo(id=374)
# 数据(作为pandas数据框)
X = appliances_energy_prediction.data.features
y = appliances_energy_prediction.data.targets
# 转换为Pandas
df = pd.concat([X, y], axis=1)
df['date'] = df['date'].apply(lambda x: x[:10] + ' ' + x[11:])
df['date'] = pd.to_datetime(df['date'])
df['month'] = df['date'].dt.month
df['day'] = df['date'].dt.day
df['hour'] = df['date'].dt.hour
df.head(3)
首先使用线性时间创建一个快速模型,作为比较的基线。
# 定义X和y
# X = df.drop(['Appliances', 'rv1', 'rv2', 'date'], axis=1)
X = df[['hour', 'day', 'T1', 'RH_1', 'T_out', 'Press_mm_hg', 'RH_out', 'Windspeed', 'Visibility', 'Tdewpoint']]
y = df['Appliances']
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 拟合模型
lr = RandomForestRegressor().fit(X_train, y_train)
# 评分
print(f'评分: {lr.score(X_train, y_train)}')
# 测试集RMSE
y_pred = lr.predict(X_test)
rmse = root_mean_squared_error(y_test, y_pred)
print(f'RMSE: {rmse}')
结果如下。
评分: 0.9395797670166536
RMSE: 63.60964667197874
接下来,对周期性时间成分(day和hour)进行编码,并重新训练模型。
# 添加周期性小时的正弦和余弦
df['hour_sin'] = np.sin(2 * np.pi * df['hour'] / 24)
df['hour_cos'] = np.cos(2 * np.pi * df['hour'] / 24)
df['day_sin'] = np.sin(2 * np.pi * df['day'] / 31)
df['day_cos'] = np.cos(2 * np.pi * df['day'] / 31)
# 定义X和y
X = df[['hour_sin', 'hour_cos', 'day_sin', 'day_cos','T1', 'RH_1', 'T_out', 'Press_mm_hg', 'RH_out', 'Windspeed', 'Visibility', 'Tdewpoint']]
y = df['Appliances']
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 拟合模型
lr_cycle = RandomForestRegressor().fit(X_train, y_train)
# 评分
print(f'评分: {lr_cycle.score(X_train, y_train)}')
# 测试集RMSE
y_pred = lr_cycle.predict(X_test)
rmse = root_mean_squared_error(y_test, y_pred)
print(f'RMSE: {rmse}')
结果如下。可以看到评分提高了1%,RMSE降低了约1个点。
评分: 0.9416365489096074
RMSE: 62.87008070927842
这个提升看似微小,但需要记住,这个示例仅使用了一个未经任何数据清洗或调优的简单模型。所观察到的效果主要源于正弦和余弦变换。
实际情况是,现实世界中的电力需求并不会在午夜重置。现在,模型终于能够捕捉到这种连续性了。
为何需要同时使用正弦和余弦
切勿陷入仅使用正弦的诱惑,因为感觉一个特征似乎就够了。用一个列代替两个列,更简洁,对吗?
遗憾的是,这会破坏对称性。在24小时制中,早上6点和下午6点可能产生相同的正弦值。不同时间具有相同编码是糟糕的,因为模型现在会混淆早高峰和晚高峰。因此,除非乐于见到混乱的预测结果,否则这并非理想选择。
同时使用正弦和余弦可以解决这个问题。两者共同为每个小时在圆上提供了一个唯一的“指纹”。可以将其想象为纬度和经度,两者缺一不可。
实际影响与结果
那么,这种方法真的对模型有帮助吗?是的,尤其对某些特定模型。
基于距离的模型
K近邻和支持向量机严重依赖距离计算。周期性编码可以防止在边界处产生虚假的“长距离”。相邻的点在特征空间中真正成为邻居。
神经网络
神经网络在平滑的特征空间中学习得更快。周期性编码消除了午夜处的尖锐不连续性。这通常意味着更快的收敛速度和更好的稳定性。
树模型
像XGBoost或LightGBM这样的梯度提升树最终可以学习到这些模式。周期性编码为它们提供了一个良好的起点。如果关注性能和可解释性,这是值得的。
何时应该使用此方法
始终要问自己一个问题:这个特征是否以周期循环的方式重复? 如果是,则考虑使用周期性编码。
常见的例子包括:
- 一天中的小时
- 一周中的星期几
- 一年中的月份
- 风向(角度)
- 任何具有循环特性的变量,都可以尝试将其编码为循环。
总结
时间不仅仅是一个数字。它是圆环上的一个坐标。
如果将其视为一条直线,模型可能会在边界处出错,并且难以理解该变量作为一个循环、重复且有规律的模式。
使用正弦和余弦进行周期性编码可以优雅地解决这个问题,它保留了邻近性,减少了人为干扰,并帮助模型更快地学习。
因此,当下次发现模型在日期变更点附近的预测表现奇怪时,可以尝试应用这个新学到的工具,让模型发挥出应有的水平。
GitHub仓库
以下是本次练习的完整代码。
https://github.com/gurezende/Time-Series/tree/main/Sine%20Cosine%20Time%20Encode
参考资料与延伸阅读
[1. 编码小时 Stack Exchange]:https://stats.stackexchange.com/questions/451295/encoding-cyclical-feature-minutes-and-hours
[2. NumPy三角函数]:https://numpy.org/doc/stable/reference/routines.math.html
[3. 关于周期性特征的实用讨论]:
https://www.kaggle.com/code/avanwyk/encoding-cyclical-features-for-deep-learning







