20世纪60年代,斯坦利·米尔格拉姆(Stanley Milgram)进行的小世界实验揭示了社会网络的奇妙特性。实验中,美国志愿者需通过熟人网络将信件递送给指定目标人物。虽然多数信件未能送达,但成功案例的平均传递次数约为6次——这便是著名的「六度分隔理论」的实证基础。
更令人惊叹的是,仅拥有10²量级社交关系的人群,竟能通过数次中转连接10⁸量级网络中的任意节点。这种现象背后的驱动力是什么?答案是启发式策略。
假设需要向芬兰的某个目标人物传递信件。若当前节点无芬兰社交关系,会选择具有瑞典居住背景的熟人作为中转,该国与芬兰毗邻的地理特征增加了成功概率。这种基于局部信息的决策策略,正是解决稀疏网络路由问题的关键。

芬兰港口景观图,来源:Illia Panasenko于Unsplash
将网络节点视作独立智能体时,每个节点的行动选择即是对消息传递路径的决策过程。这种具有状态转移特性的问题天然适合采用强化学习框架解决。
问题建模
给定稀疏有向图结构,节点平均出度远小于总节点数,且边权重代表传输成本。目标在于设计强化学习算法,使其能在任意起点与终点间找到近似最优路径(若可达)。经典解法如Dijkstra算法虽能求得精确解,但需全局拓扑信息——这正是分布式Q学习方案的价值所在。
分布式Q学习框架
Q学习通过维护状态-动作价值矩阵(Q矩阵)实现策略优化,其更新规则为:
Q(i,j)←(1–α)Q(i,j)+α(r+γ max l Q(k,l))
其中α为学习率,γ为折扣因子。针对稀疏图特性,采用节点分布式架构:
- 每个节点作为独立智能体,维护目标节点为行、出边为列的Q矩阵
- 状态空间压缩为节点数N,而非传统N²维度
- 消息传递仅需携带目标节点信息,降低通信开销
代码实现
核心类QNode定义节点智能体:
class QNode:
def __init__(self, number_of_nodes=0, connectivity_average=0, connectivity_std_dev=0, Q_arr=None, neighbor_nodes=None,
state_dict=None):
if state_dict is not None:
self.Q = state_dict['Q']
self.number_of_nodes = state_dict['number_of_nodes']
self.neighbor_nodes = state_dict['neighbor_nodes']
else:
... # 初始化邻居节点与Q矩阵
def epsilon_greedy(self, target_node, epsilon):
... # ε-贪婪策略实现实验结果
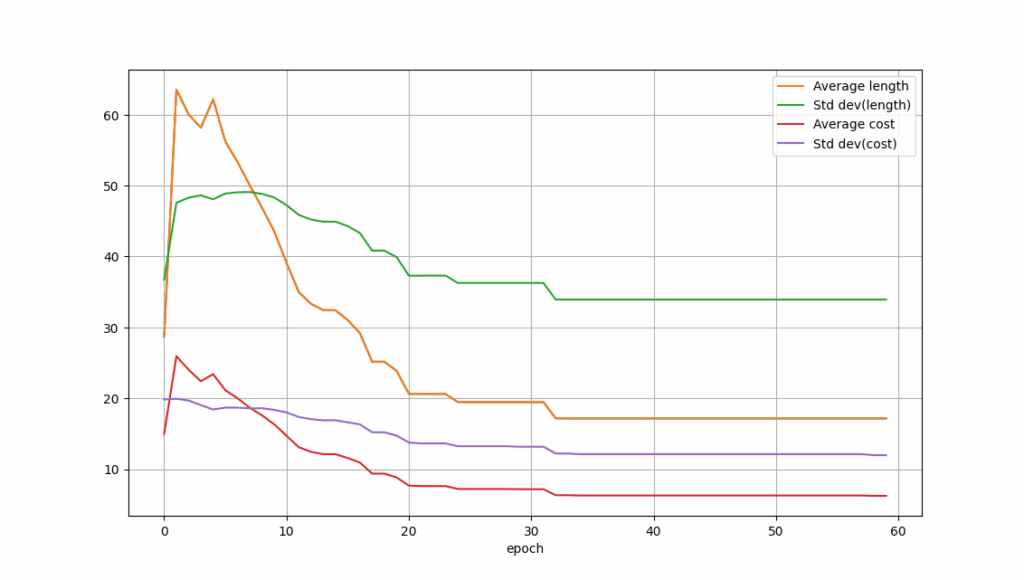
在12节点测试图上,训练过程中路径成本与跳数变化趋势如图示:
节点4的Q矩阵收敛情况示例:
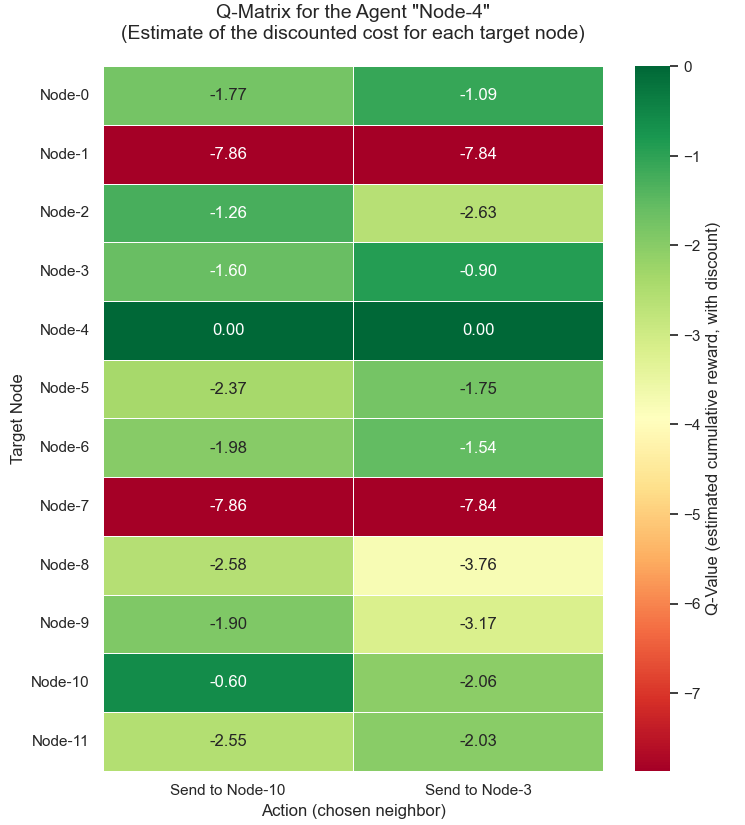
实例测试表明,该方案在多数场景下接近Dijkstra算法的最优解,例如节点4→11路径[4,3,5,11]成本2.1与经典算法一致。部分复杂路径存在微小差距,如节点6→9路径成本3.5 vs 理论最优3.4,体现了迭代算法的特性。
应用价值
该框架将小世界实验抽象为稀疏图路由问题,通过分布式Q学习实现去中心化路径优化。代码已开源GitHub仓库,为通信网络、物流调度等领域提供新思路。
*注:原始小世界实验实际仅在美国本土进行,芬兰案例为概念延伸